 |
Главная |
Общие правила составления двойственных задач
|
из
5.00
|
При составлении двойственных задач используют следующие правила:
Правило 1. Во всех ограничениях исходной задачи свободные члены должны находится в правой части, а члены с неизвестными – в левой.
Правило 2. Ограничения-неравенства исходной задачи должны быть записаны так, чтобы знаки неравенств у них были направлены в одну сторону.
Правило 3. Если знаки неравенств в ограничениях исходной задачи «≥», то целевая функция  должна максимизироваться, а если «≤», то минимизироваться.
должна максимизироваться, а если «≤», то минимизироваться.
Правило 4.Каждому ограничению исходной задачи соответствует неизвестное в двойственной задаче; при этом неизвестное, отвечающее ограничению-неравенству, должно удовлетворять условию неотрицательности, а неизвестное, отвечающее ограничению-неравенству, может быть любого знака.
Правило 5. Целевая функция двойственной задачи имеет вид:  где
где  -свободный член целевой функции Z(X) исходной задачи;
-свободный член целевой функции Z(X) исходной задачи;  - свободные члены в ограничениях исходной задачи, при этом
- свободные члены в ограничениях исходной задачи, при этом  -свободный член именно того ограничения, которому соответствует неизвестная
-свободный член именно того ограничения, которому соответствует неизвестная  неизвестные в двойственной задаче.
неизвестные в двойственной задаче.
Правило 6. Целевая функция F(Y) двойственной задачи должна оптимизироваться противоположным по сравнению с Z(X) образом, т.е. если  то
то  и если
и если  то
то 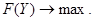
Правило 7. Каждому неизвестному  исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих nограничений (вместе с условиями неотрицательности неизвестных
исходной задачи соответствует ограничение в двойственной задаче. Совокупность этих nограничений (вместе с условиями неотрицательности неизвестных  , соответствующих ограничениям-неравенствам исходной задачи) образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными
, соответствующих ограничениям-неравенствам исходной задачи) образует систему ограничений двойственной задачи. Все ограничения двойственной задачи имеют вид неравенств, свободные члены которых находятся в правых частях, а члены с неизвестными  в левых. Все знаки неравенств имеют вид «≥», если
в левых. Все знаки неравенств имеют вид «≥», если  и «≤», если
и «≤», если 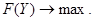
Коэффициенты, с которыми неизвестные 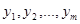 входят в ограничение, соответствующее неизвестному
входят в ограничение, соответствующее неизвестному  совпадают с коэффициентами при этом неизвестном
совпадают с коэффициентами при этом неизвестном  в ограничениях исходной задачи, а именно: коэффициент при
в ограничениях исходной задачи, а именно: коэффициент при  совпадает с тем коэффициентом при
совпадает с тем коэффициентом при  , с которым
, с которым  входит в ограничение исходной задачи, соответствующее неизвестному
входит в ограничение исходной задачи, соответствующее неизвестному  .
.
Взаимная симметрия прямой и двойственной задач определяет существование определенного соответствия между их оптимальными решениями, которое устанавливают теоремы двойственности: если прямая и двойственная задачи линейного программирования имеют оптимальные решения, то экстремальные значения их целевых функций равны, т.е. справедливо равенство:
min CX = max YB. (первая теорема двойственности)
Не менее важное соответствие оптимальных решений прямой и двойственных задач устанавливают условия дополняющей нежесткости, которые связывают необходимые и достаточные условия оптимальности допустимых решений X и Yобеих задач со следующими соотношениями:
Y(AX-B)=0 (C-YA)X=0. (вторая теорема двойственности)
Таким образом всегда имеется возможность выбора: решать прямую или двойственную задачу, используя модификацию задачи, для которой легче найти решение.
Пример. Составить задачу, двойственную к данной:

Р е ш е н и е. Используем общие правила составления двойственных задач. Умножим ограничения-неравенства на -1, так как в задаче на минимум они должны иметь вид «≥» (см. правило 3). Исходная задача запишется в виде:

Составим двойственную задачу:
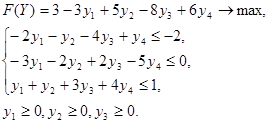
Неизвестная  соответствующая ограничению-неравенству, может быть любого знака (см. правило 4).
соответствующая ограничению-неравенству, может быть любого знака (см. правило 4).
 5. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ОБЩЕЙ РАСПРЕДЕЛИТЕЛЬНОЙ ЗАДАЧИ.
5. ТРАНСПОРТНАЯ ЗАДАЧА ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ КАК ЧАСТНЫЙ СЛУЧАЙ ОБЩЕЙ РАСПРЕДЕЛИТЕЛЬНОЙ ЗАДАЧИ.
|
из
5.00
|
Обсуждение в статье: Общие правила составления двойственных задач |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

