Пример расчетов задач по теме «косой изгиб»

Интеграл Мора

 

Метод Мора – это универсальный способ для определения линейных и угловых перемещений в любых плоских и пространственных системах, состоящих из шарнирно или жестко соединенных прямых или кривых брусьев.

При отыскании линейного перемещения к системе, освобожденной от заданных нагрузок, в направлении искомого перемещения (в заданной точке) прикладывается безразмерная единичная сила. Аналогично, при определении углового перемещения в сечении, поворот которого требуется найти, прикладывается пара сил (в плоскости искомого поворота) с моментом, равным безразмерной единице.

Ограничиваясь рассмотрением плоских систем – балок и плоских рам и учитывая только энергию деформации, связанную с изгибающими моментами (т.е. пренебрегая для балок энергией, связанной с наличием поперечных сил, а для рам – поперечных и продольных сил), получают следующую формулу для определения перемещений, правую часть которой называют интегралом Мора:

 

 

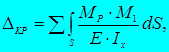
где Δ_KP – искомое линейное или угловое перемещение. Первый индекс «K» указывает точку и направление искомого перемещения, второй индекс – причину, вызывающую это перемещение. Индекс «P» означает, что определяется перемещение от заданных нагрузок.

M_P и M₁ – аналитические выражения изгибающих моментов от заданной нагрузки и единичной силы (момента).

В некоторых случаях удобно заменять индекс «1» буквенным индексом, указывающим наименование сечения (точки), перемещение которого определяется.

Результат расчета интеграла мора дает угловое перемещение в радианах. Знак суммы указывает на то обстоятельство, что в общем случае, когда уравнения «грузового» M_P и «единичного» M₁ моментов для отдельных участков различны, интеграл вычисляется по участкам и результаты суммируются.

Формула применима для вычислений перемещений как в системах, состоящих из прямых брусьев, так и из брусьев малой кривизны.

Брусья малой кривизны – это брусья, для которых отношение радиуса кривизны ρ их оси к высоте h поперечного сечения не менее двух:

 

 

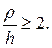
Для прямых брусьев дифференциал дуги dS заменяется на dz.

В случаях, когда ось бруса прямолинейна и жесткость поперечного сечения в пределах отдельных участков постоянна, интеграл Мора целесообразно вычислять графо-аналитическим методом, применяя правило Верещагина. По этому правилу интеграл Мора для отдельного участка балки или рамы вычисляется как произведение площади нелинейной эпюры изгибающих моментов на ординату линейной эпюры изгибающих моментов, взятую под центром тяжести нелинейной, деленное на жесткость поперечного сечения данного участка:

 

 

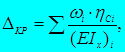
где ω_i – площадь нелинейной эпюры изгибающих моментов;

η_Ci – ордината линейной эпюры изгибающих моментов, соответствующая центру тяжести нелинейной;

(EI_x)_i – жесткость поперечного сечения данного участка бруса.

В случае, когда на данном участке обе эпюры линейны, безразлично, на какой из них брать площадь, на какой – ординату.

Произведение ω_iη_i считается положительным, если часть эпюры, имеющая площадь ω_i, и соответствующая ордината η_i расположены по одну сторону от оси бруса.

При применении метода Мора положительное значение искомого перемещения получается в случае, если его направление совпадает с направлением приложенной единичной силы (момента).

При непосредственном (аналитическом) вычислении интеграла Мора протяженность каждого участка при постоянной жесткости сечения EI_x определяется областью, в пределах которой закон изменения как «грузового» M_P, так и «единичного» M₁ моментов остается постоянным. При применении правила Верещагина участком является часть балки (элемента рамы), в пределах которой хотя бы одна из эпюр меняется по монотонному линейному закону. Линейность эпюры надо понимать в строго математическом смысле. В частности, эпюра, состоящая из двух прямолинейных отрезков («ломаная» эпюра), должна рассматриваться как состоящая из дух отдельных линейных эпюр.

 

Всегда есть возможность разбить прямой брус на такие участки, в пределах каждого из которых одна из эпюр (чаще «единичная») линейна.

 

 

Значения площадей эпюр и координат их центров тяжести:

а) Горизонтальная линия.

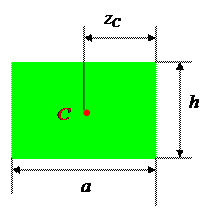
ω = a ∙ h;

 

 

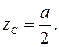
б) Наклонная линия.

 

 

 

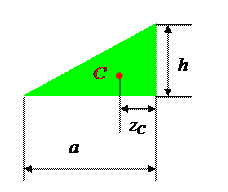
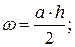
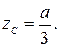
в) Квадратичная парабола.

 

 

 

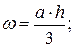
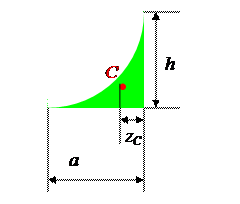
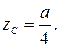
г) Квадратичная парабола.

 

 

 

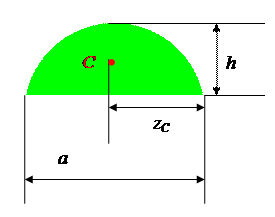
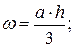
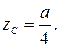
д) Кубическая парабола.

 

 

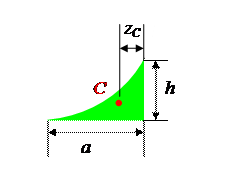
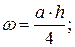
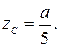
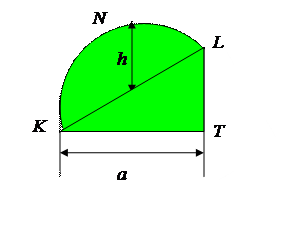е) Если одна из эпюр представляет собой несимметричную квадратичную параболу, а вторая эпюра линейна, то соединяют прямой точки K и L. Площадь эпюры распадается на две части. Площадь и положение центра тяжести треугольника KLT известны. Площадь параболического сегмента KNL вычисляется по формуле

 

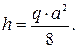
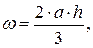
где a – длина отрезка KT, q – интенсивность равномерно распределенной нагрузки, действующей на участке бруса, для которого построена эпюра. Центр тяжести этой части соответствует середине отрезка KT.

При определении перемещений в плоских системах может возникнуть необходимость в учете потенциальной энергии деформации, связанной не только с изгибающими моментами, но и обусловленной наличием поперечных и продольных сил. В этих случаях формула для перемещений (интеграл Мора) принимает вид:

 

 

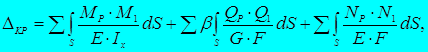
где Q_P и Q₁ – аналитические выражения поперечной силы соответственно от заданной нагрузки и от единичной силы (момента);

N_P и N₁ – аналитические выражения продольной силы соответственно от заданной нагрузки и от единичной силы (момента);

β – коэффициент, отражающий неравномерность распределения касательных напряжений по поперечному сечению. Для прямоугольника β = 1,2; для круга β = 10/9.

Вычисление интеграла Мора может быть выполнено по правилу Верещагина:

 

 

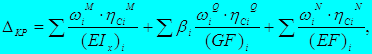
где ω_i^M, ω_i^Q и ω_i^N – площади нелинейных эпюр соответственно изгибающих моментов, поперечных и продольных сил;

η_Ci^M, η_Ci^Q и η_Ci^N – ординаты линейных эпюр изгибающих моментов, поперечных и продольных сил, соответствующие центрам тяжести нелинейных эпюр изгибающих моментов, поперечных и продольных сил.

 

Пример расчетов задач по теме «косой изгиб»

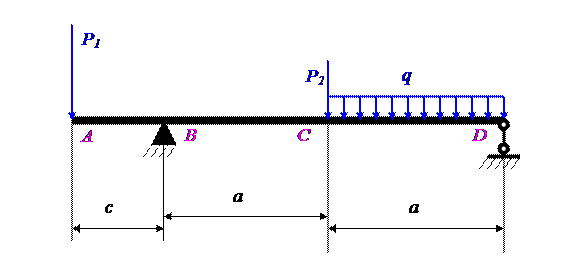
Задача 9.

Для заданной балки требуется:

3) определить величину и направление полного прогиба в сечении под силой P₁.

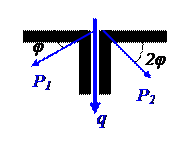
a = 2,0 м; P₁ = 4 кН; двутавр №30;

c = 0,6 м; P₂ = 2 кН; швеллер №22;

φ = 10⁰; q = 2 кН/м; уголок 200х200х16;

[σ] = 160 МПа;

b = 200 мм = 20 см;

y₀ = z₀ = 5,54 см;

A₁ = 61,98 см²;

I_y1 = I_z1 = 2362,67 см⁴; I_z = 4725,14 см⁴; I_y = 8529,671 см⁴;

A = 123,96 см²;

W_z = 589,88 · 10^-6 м³; W_y = 236,257 · 10^-6 м³.

 

 

 

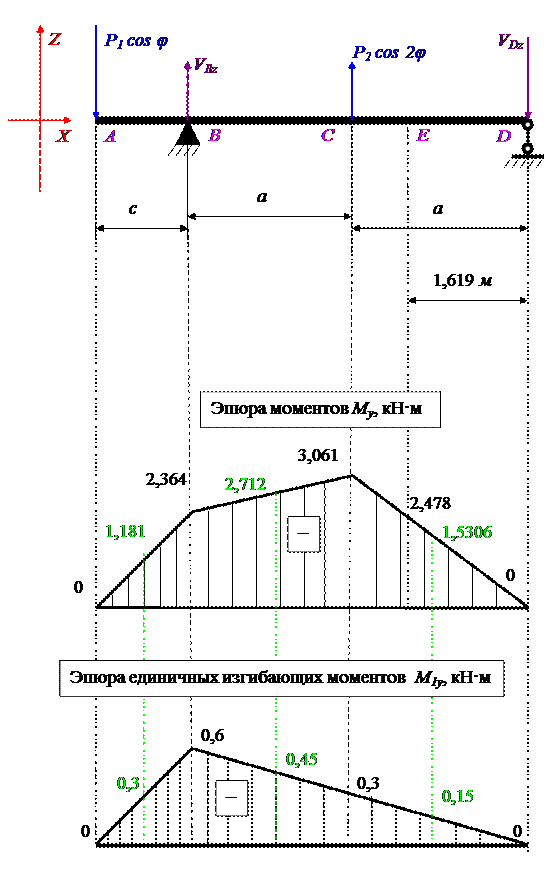
Совместно эпюры выглядят так:

 

 

 

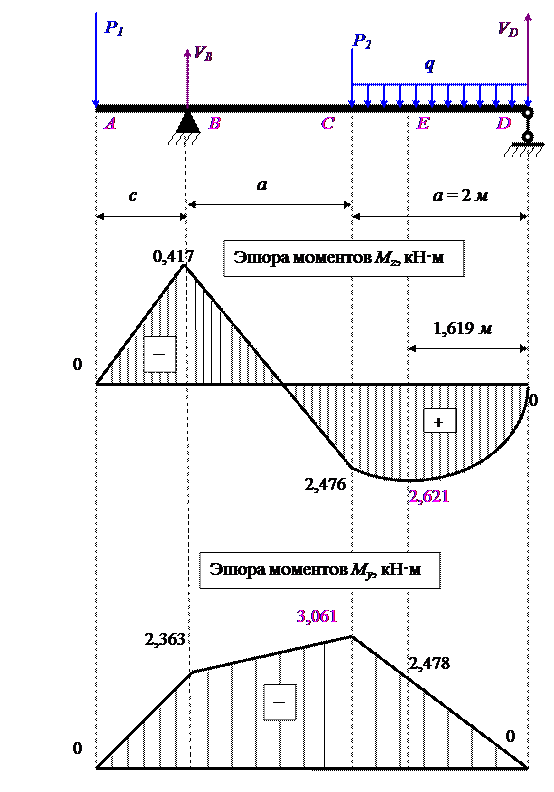
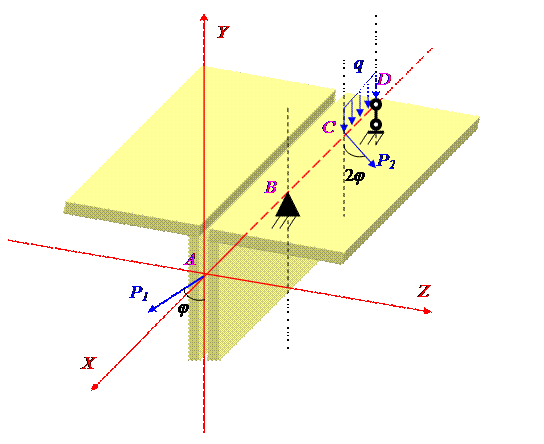
y = 0,68485 z – уравнение нейтральной линии.

Угол наклона нейтральной линии β = 34,4⁰.

Эпюра нормальных напряжений и нейтральная линия:

 

 

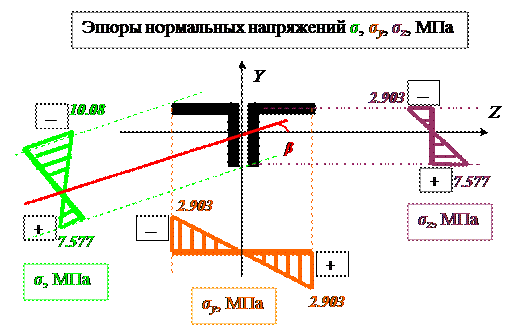
3) Определим величину и направление полного прогиба в сечении под силой P₁.

а) Найдем прогиб δ_y вдоль оси Y. Для этого сечение под силой P₁ нагружаем единичной безразмерной силой.

 

 

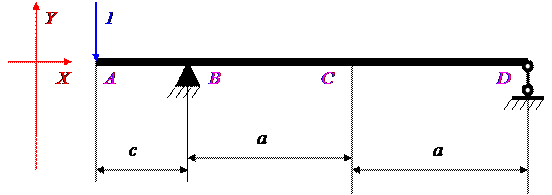
Определим опорные реакции V_By и V_Dy.

 

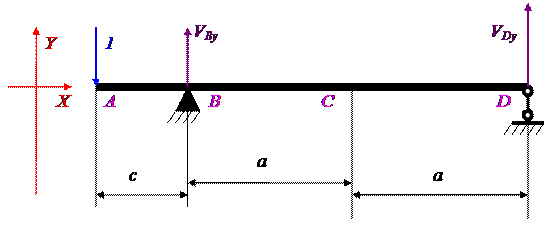
Сумма моментов сил относительно точки B равна нулю:

2a ∙ V_Dy + c ∙ 1 = 0;

2 ∙ 2 ∙ V_Dy + 0,6 ∙ 1 = 0;

V_Dy = – 0,15.

Сумма моментов сил относительно точки D равна нулю:

2a ∙ V_By – (2a + c) ∙ 1 = 0;

2 ∙ 2 ∙ V_By – (2 ∙ 2 + 0,6) ∙ 1 = 0;

V_By = 1,15.

Строим эпюру единичных изгибающих моментов M_1z методом сечений.

 

 

 

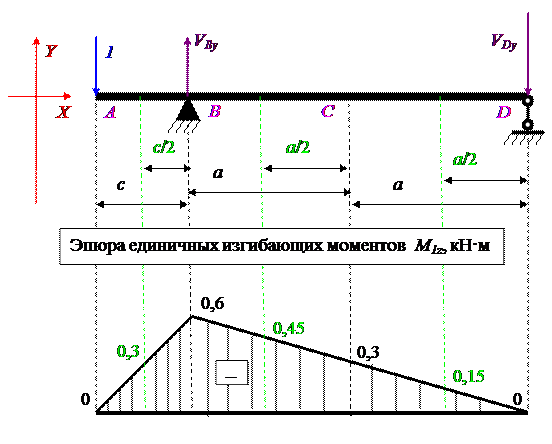
Прогиб δ_y считаем по интегралу Мора:

 

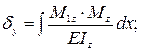
δ_y = δ_yAB + δ_yBC + δ_yCD

 

 

 

 

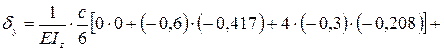
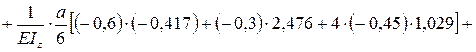
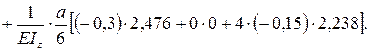
Значения подставляем в системе СИ.

 

 

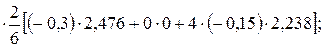
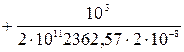
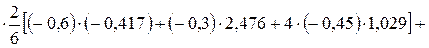
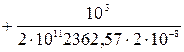
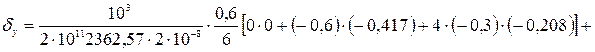
δ_y = –0,0001515 м.

 

б) Найдем прогиб δ_z вдоль оси Z. Для этого сечение под силой P₁ нагружаем единичной безразмерной силой. Схема аналогична предыдущей схеме.

 

 

 

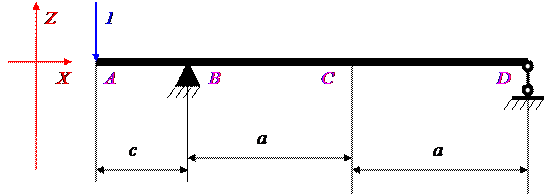
Определим опорные реакции V_Bz и V_Dz.

 

 

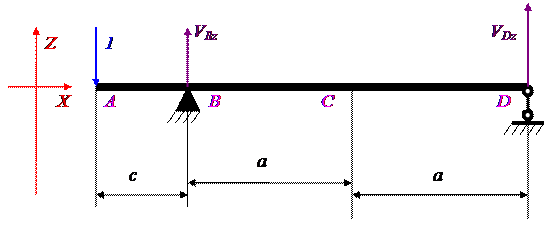
Сумма моментов сил относительно точки B равна нулю:

2a ∙ V_Dz + c ∙ 1 = 0;

2 ∙ 2 ∙ V_Dz + 0,6 ∙ 1 = 0;

V_Dz = – 0,15.

 

Сумма моментов сил относительно точки D равна нулю:

2a ∙ V_Bz – (2a + c) ∙ 1 = 0;

2 ∙ 2 ∙ V_Bz – (2 ∙ 2 + 0,6) ∙ 1 = 0;

V_Bz = 1,15.

 

 

Строим эпюру единичных изгибающих моментов M_1y методом сечений.

 

 

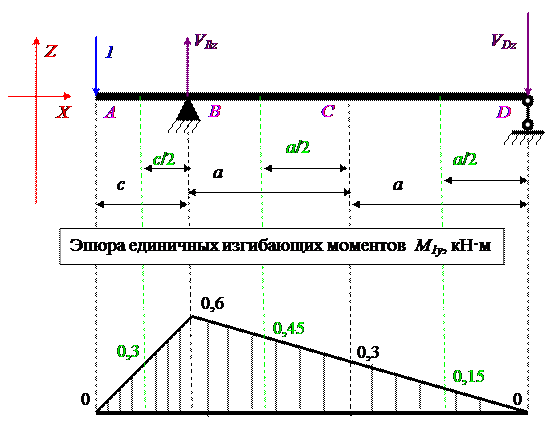
Прогиб δ_z считаем по интегралу Мора:

 

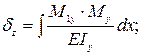
δ_z = δ_zAB + δ_zBC + δ_zCD;

 

 

 

 

 

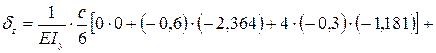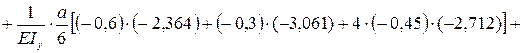
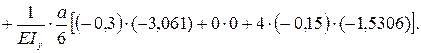
δ_z = 0,000193 м.

 

 

Полный прогиб считаем по теореме Пифагора:

 

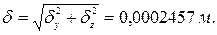
Можно перевести в сантиметры.