Формулы ошибок простой случайной выборки

	Способ отбора единиц
Повторный	бесповторный
Средняя ошибка µ для средней   для доли
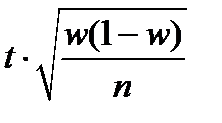
Предельная ошибка Для средней     Для доли	= t 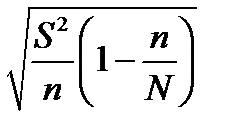  =	= t = t

Формулы предельной ошибки позволяют решать задачи трех видов.

1. Определение пределов генеральных характеристик с заданной степенью надежности (доверительной вероятностью) на основе показателей, полученных по данным выборки.

Доверительные интервалы для генеральной средней:

х_ср. ±

х_ср. - ≤ ≤ х_ср. + .

Доверительные интервалы для генеральной доли:

р = w

w - ≤ р ≤ w +

Пример.1.

Из партии электроламп взята 20%-я случайная бесповторная выборка для определения среднего веса спирали. Результаты выборки следующие (табл. 4.5).

Таблица 4.5

Определить с вероятностью 0,95 доверительные пределы, в которых лежит средний вес спирали для всей партии электроламп.

Решение

Доверительные интервалы для генеральной средней с вероятностью Р:

х_ср. - ≤ ≤ х_ср. + .

где х_ср. — средний уровень признака по выборке:

х_ср. = 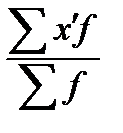= (39*15+41*30+43*45+45*10)/(15+30+45+10) = 4200/100 = 42,0 мг;

t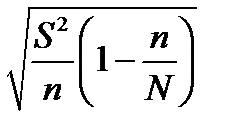 ,N = 100/0.2 = 500.

При вероятности Р = 0,95 t = 1,96 (по статистическим таблицам).

= ((39 - 42)² • 15+(41 - 42)² • 30+(43 -42)² • 45+(45 - 42)² • 10)/100 = 300/100 = 3,0.

t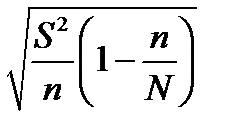= 1,96* =0,3 мг

Доверительные интервалы для генеральной средней с вероятностью Р = 0,95:

42,0-0,3 42,0+0,3, 41,7 мг 42,3 мг

Пример. 2.

На заводе электроламп из партии продукции в количестве 16 000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными.

Определить с вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции.

Решение

Определяется доля бракованной продукции по выборке:

w = 40/1600 = 0.025, или 2,5%.

При вероятности Р = 0,997 имеем t = 3,0 (по таблицам). Размер предельной ошибки:

=3,0 = 3,0*0,0037=0,011 или 1,1%.

Доверительные интервалы для генеральной доли с вероятностью Р= 0,997:

2,5 – 1,1≤ р ≤ 2,5+1,1, 1,4% ≤ р ≤ 3,6%

2. Определение доверительной вероятности того, что генеральная характеристика может отличаться от выборочной не более, чем на определенную заданную величину.

Доверительная вероятность Р является функцией от t, определяемой по формуле

t =

По величине t определяется доверительная вероятность Р c использованием стат. таблиц.

Пример. 3.

По городской телефонной сети в порядке случайной выборки (механический отбор) произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 5 мин при среднем квадратическом отклонении 2 мин.

Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18с?

Решение

По условию задачи известны:

объем выборки – n=100;

выборочная средняя – х_ср. = 5 мин

выборочное среднее квадратическое отклонение – S = 2 мин

предельная ошибка выборки - = 18с = 0,3 мин.

; = = 0,2мин; = 0,3/0,2 = 1,5.

Затем по статистическим таблицам на основе значения t = 1,5 определяется вероятность того, что ошибка не превысит заданной величины. При t =1,5 вероятность Р = 0,866.

3. Определение необходимого объема выборки, который с практической вероятностью обеспечивает заданную точность выборки.

Для расчета объема выборки необходимо иметь следующие данные:

a) размер доверительной вероятности (Р);

b) коэффициент t , зависящий от принятой вероятности (определяется по стат. таблицам);

c) величину σ² (или pq, причем q=1-р) в генеральной совокупности; они заменяются величинами, полученными в предшествующих обследованиях или при пробных выборках [S² или w(l—w)];

d) величину максимально допустимой ошибк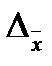и ( или );

e) объем генеральной совокупности (N).

Необходимый объем выборки определяется на основе допустимой величины ошибки:

= t ,или = tµ_р .

В табл. 4.2 приведены формулы для расчета численности простой случайной выборки.

Табл.4.2