ФОРМУЛЫ ДЛЯ РЕШЕНИЯ ЗАДАЧ

 

«Сводка и группировка статистических данных»

(задача №1)

 

Сводка и группировка – важные этапы в экономико-статистических исследованиях.

Статистическая сводка – это обработка материалов наблюдения для получения обобщающих (сводных) показателей.

С помощью простой сводки представляют общие итоги по изучаемой совокупности в целом без предварительной систематизации собранных данных.

Статистическая группировка – это разделение статистической совокупности на однородные группы по существенным признакам. Различают типологические, структурные и аналитические группировки.

При образовании групп с равными интервалами применяется формула:

h = ,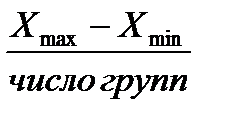

где h – величина интервала;

X max – максимальное значение признака;

X min – минимальное значение признака.

 

«Абсолютные и относительные величины. Графические способы изображения статистических данных»

(задачи №1 – №6)

 

Абсолютные величины – это показатели, характеризующие размеры, объёмы изучаемых явлений. Абсолютные величины могут иметь единицы измерения:

- натуральные (кг, т, л, пары, штуки и т.д.);

- денежные (стоимостные);

- трудовые (человеко-часы, человеко-дни и т.д.).

Для учёта товаров, состоящих из нескольких разновидностей одного и того же товара (одной и той же потребительской стоимости), прибегают к условно-натуральным единицам измерения. Такие единицы получают, приводя отдельные виды товара к одному, принятому за основу (эталон).

Объём продукции из натуральных единиц в условно-натуральные исчисляется по формуле: Q усл.-нат. = Q нат. × К, где

Q – объём продукции;

K – коэффициент пересчёта.

Относительная величина – это частное от деления двух статистических величин, которое характеризует количественное соотношение между ними. При этом в числителе всегда будет сравниваемый показатель, а в знаменателе – показатель, с которым производится сравнение.

Расчёт относительных величин:

относительная величина выполнения плана =

= ;

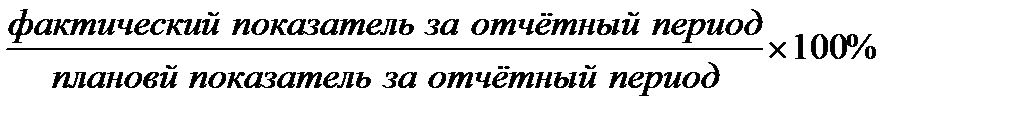относительная величина планового задания =

= ;

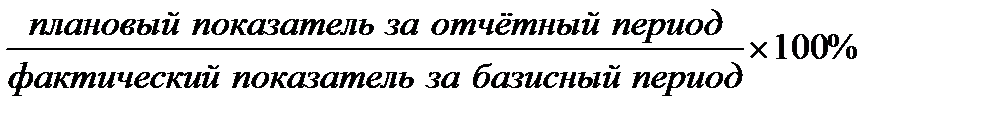относительная величина структуры (удельный вес) =

= ;

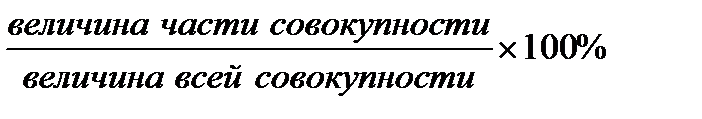относительная величина динамики =

= .

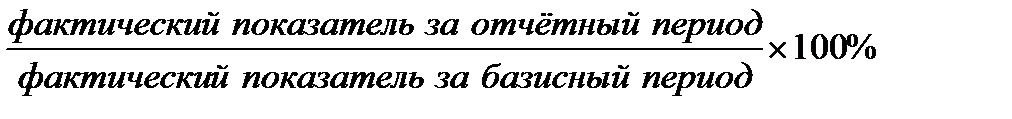Взаимосвязь относительных величин:

Относительная Относительная Относительная

величина = величина × величина

динамики планового задания выполнения плана

 

График (диаграмма) – это условное изображение (чертёж) статистических данных с помощью геометрических знаков и фигур для наглядности. График должен иметь экспликацию, т.е. пояснение его содержания: заголовок, масштабную шкалу, цифровое обозначение шкалы и указание единиц измерения.

Виды диаграмм: линейные, столбиковые, полосовые и круговые.

 

«Средние величины и показатели вариации»

(задачи №7 – №12)

 

Средняя величина – это обобщающий показатель статистической совокупности, выражающий типический уровень изучаемого признака.

 

Средняя арифметическая применяется в том случае, если известны варианты (х), т.е. индивидуальные значения признака и частоты (f), т.е. количество отдельных вариантов, в том числе:

а) средняя арифметическая простая (невзвешенная) применяется в том случае, если значение признака встречается только один раз или частоты (f) равны между собой:

= ;

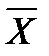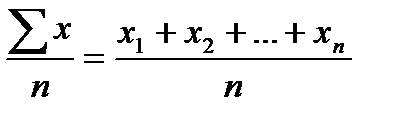б) средняя арифметическая взвешенная применяется в том случае, если частоты (f) не равны между собой:

= .

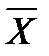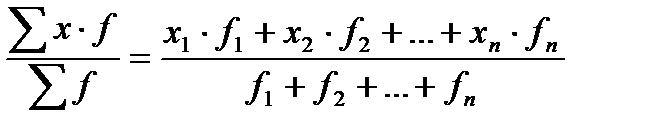Средняя гармоническая применяется в том случае, если неизвестны частоты, а даны лишь варианты (х) и произведения вариант на частоты (М), в том числе:

а) средняя гармоническая простая (невзвешенная) применяется в том случае, если М равны между собой:

= ;

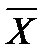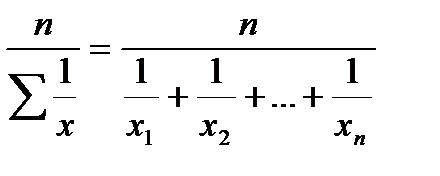б) средняя гармоническая взвешенная применяется в том случае, если М не равны между собой:

= = .

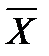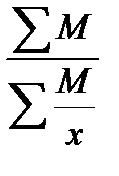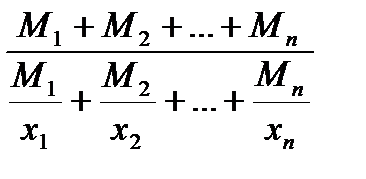Структурные средние:

а) мода (Мо) – чаще всего встречающийся вариант;

б) медиана (Ме) – вариант, который делит упорядоченный (ранжированный) ряд на две равные части.

 

Вариация – это различие индивидуальных значений признака внутри изучаемой совокупности.

Показатели вариации:

Размах = (X max – X min) – отображает колеблемость только двух крайних по значению вариантов.

Дисперсия: σ² = 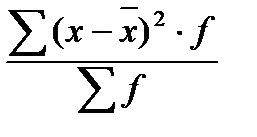– безмерная величина, экономического значения не имеет.

Среднее квадратическое отклонение: σ = 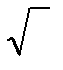σ² – характеризует меру колеблемости в абсолютных величинах.

Коэффициент вариации: V = 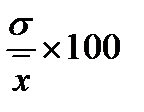% – характеризует меру колеблемости в %.

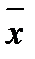– осредняемый признак.

 

«Ряды динамики»

(задачи №13 – №16)

Основная цель статистического изучения динамики – выявление и измерение закономерностей развития изучаемого явления во времени, что возможно с помощью построения и анализа статистических рядов динамики.

Различают:

а) интервальный ряд динамики – отображает итоги развития явления за отдельные периоды (интервалы) времени;

б) моментный ряд динамики – отображает состояние явления на определённые даты (моменты) времени.

 

Применяют:

а) базисный способ сравнения уровней, когда каждый последующий уровень (Уn) сравнивается с одним и тем же базисным уровнем (У0);

б) цепной способ сравнения уровней, когда каждый последующий уровень (Уn) сравнивается с предыдущим уровнем (Уn-1).

 

Расчёт показателей ряда динамики

 

Базисный способ	Цепной способ
Абсолютный прирост
ΔУ = Уn – У0	ΔУ = Уn – Уn-1
Темп роста (%)
Т рост = 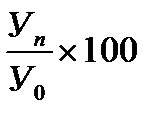%	Т рост = %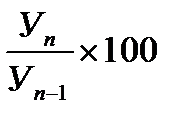
Темп прироста (%)
Т прирост = Т рост – 100%	Т прирост = Т рост – 100%
Абсолютное значение 1% прироста

 

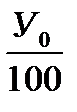
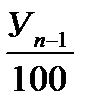
Средний уровень рассчитывается:

а) для интервального ряда динамики – по средней арифметической простой:

;

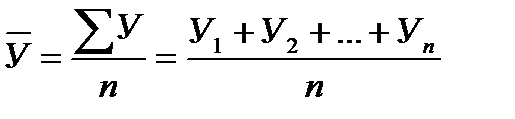б) для моментного ряда динамики с равностоящими показателями времени –
по средней хронологической:

;

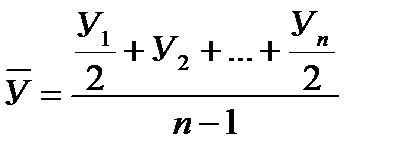в) для моментного ряда динамики с неравностоящими показателями времени –
по средней арифметической взвешенной:

,

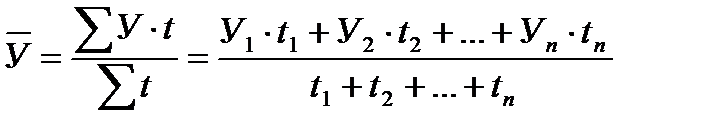где t – количество времени (дни, месяцы, годы) между датами.

Средний абсолютный прирост (Δ 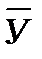) характеризует обобщающую величину индивидуальных абсолютных приростов:

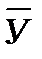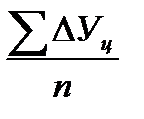Δ = или Δ = ,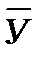

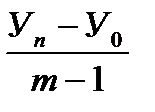где Уn и У0 – конечный и начальный уровни ряда;

m – число субпериодов времени в ряду динамики.

 

Средний темп роста ( 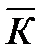рост) характеризует обобщающую величину индивидуальных темпов роста и вычисляется по формуле средней геометрической:

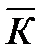рост = 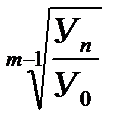; 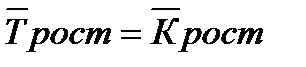× 100%

или 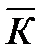рост = ,

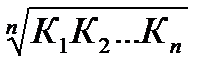где 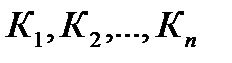– индивидуальные цепные темпы роста (в коэффициентах);

п – число индивидуальных темпов роста.

 

Средний темп прироста ( 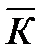прирост) вычисляется следующим образом:

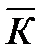прирост = 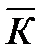рост – 1 или .

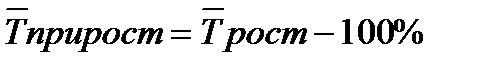«Индексы»

(задачи №17 – №25)

Индексы широко используются в экономических исследованиях. С их помощью изучается изменение объёма поступления и реализации товаров, уровня цен, издержек производства и обращения и т.д.

Индекс – это относительная величина сравнения сложных статистических совокупностей и отдельных их единиц.

Сложная совокупность – это совокупность, отдельные элементы которой нельзя обобщить непосредственно суммированием. Например, ткань (в метрах), костюмы (в штуках), обувь (в парах) и т.д.

 

Индивидуальные индексы (i) – характеризуют изменение отдельных единиц сложной совокупности:

а) физического объёма товарооборота: iq = ,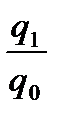

где q₁, q₀ – количество проданных товаров в текущем и базисном периодах.

б) цены: ip = ,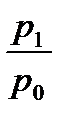

где p₁, p₀ – цена за единицу товара в текущем и базисном периодах.

 

Аналогично можно рассчитать индивидуальные индексы численности, производительности труда, себестоимость и др.

 

Общие индексы (I) выражают обобщающие результаты изменения всех единиц сложной совокупности:

1) агрегатная форма общих индексов применяется в том случае, если даны и цена, и количество за оба сравниваемых периода:

а) агрегатный индекс физического объёма товарооборота: Iq = ;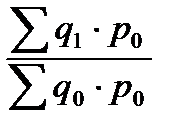

б) агрегатный индекс цены: Ip = ;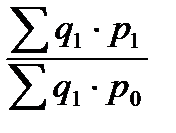

в) индекс товарооборота в фактических ценах: Ipq = .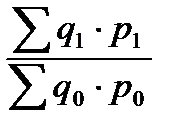

 

2) Средний арифметический индекс физического объёма товарооборота применяется в том случае, если известны индивидуальные индексы физического объёма (iq) и товарооборот базисного периода (q0p0): Iq = .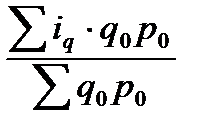

3) Средний гармонический индекс цен применяется в том случае, если известны индивидуальные индексы цен (ip) и товарооборот отчётного периода (q1p1):

Ip =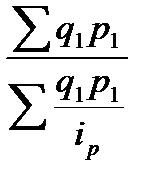

Взаимосвязь индексов:

1) в относительных величинах: Ipq = Iq × Ip; Iq = 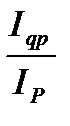; Ip = ;

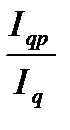2) в абсолютных величинах:

общее изменение товарооборота в фактических ценах в отчётном периоде по сравнению с базисным периодом: Δqp = Σ q₁p₁ – Σ q₀p₀;

в том числе:

- за счёт изменения физического объёма продажи товаров:

∑Δqp(q) = Σq₁p₀ – Σq₀p_0;

 

- за счёт изменения цен: ∑Δqp(p) = Σq₁p₁ – Σq₁p_0.

 

Разность между числителем и знаменателем агрегатного индекса цен
(Σq₁p₁ – Σq₁p₀) представляет собой экономический показатель, характеризующий сумму экономии (знак «–») или перерасхода (знак «+»), полученную населением в связи с покупками в отчётном периоде по изменённым ценам.

 

Эластичность спроса по цене характеризует реагирование спроса на изменение цен:

Коэффициент эластичности спроса = .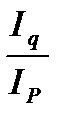

Индекс покупательной способности рубля = .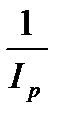

ЗАДАЧИ

Задача №1. Товарооборот 10 магазинов за отчётный период характеризуется данными таблицы, тыс. руб.:

№ магазина	План	Факт
ВСЕГО

 

Требуется:

1) произвести группировку по уровню выполнения плана, выделив 3 группы:

не выполнившие, выполнившие и перевыполнившие план;

2) вычислить процент выполнения плана по каждому магазину, по каждой группе и в целом.

Группировку оформить в таблице.

 

Задача №2. Розничный товарооборот магазина характеризуется данными таблицы, тыс. руб.:

 

Товарные группы	Базисный период	Отчётный период
Продовольственные Непродовольственные
ВСЕГО

Вычислить:

1) относительные величины динамики (в %) каждой товарной группы и общего объёма товарооборота;

2) структуру товарооборота (в %) в базисном и отчётном периодах.

 

Задача №3. Планом на отчётный период предусматривалось увеличить производительность труда на 7,5%. Фактически по сравнению с предыдущим периодом производительность труда увеличилась на 12%.

Определить процент выполнения плана по росту производительности труда.

 

Задача №4. В отчётном периоде план по выпуску продукции перевыполнен на 4,5%. Фактический выпуск продукции по сравнению с прошлым годом возрос на 9,3%. Определить относительную величину планового задания (в %).

 

Задача №5. Для хозяйственных нужд предприятие заготовило следующие виды топлива:

 

Виды топлива	Единица измерения	Калорийность ккал/кг	Заготовлено
Базисный год	Отчётный год
Уголь	т		7,5	7,5
Торф	т		2,1	2,9
Дрова	куб. м		13,0	12,4

 

Требуется:

1) пересчитать всё заготовленное топливо в условное (дрова);

2) вычислить относительные величины динамики (в %) заготовки отдельных видов топлива и их общего объёма.

Задача №6. За отчётный период магазином было реализовано 150 тетрадей 12-ти листовых, 80 тетрадей 24-х листовых, 35 тетрадей 48-ми листовых и 10 тетрадей 96-ти листовых. Определить общий объём реализации тетрадей.

 

Задача №7. В результате проведённого статистического наблюдения в магазине получены следующие данные о продаже мужской обуви:

 

Размер обуви
Число продаж (пар)

 

Определить средний размер обуви и модульную величину.

Задача №8. На основании данных таблицы вычислить среднюю заработную плату 1-го работника предприятия за каждый месяц.

 

Январь	Апрель
Зарплата (руб.)	Число работников (чел.)	Зарплата (руб.)	Фонд оплаты труда (руб.)

Задача №9. По данным о распределении работников предприятия по стажу работы:

 

Стаж (лет)					12,5
Число работников (чел.)

 

Определить:

1) моду и медиану;

2) средний стаж 1-го работника;

3) среднее квадратическое отклонение;

4) коэффициент вариации.

 

Задача №10. На основании данных таблицы вычислить среднюю заработную плату 1-го работника по каждому отделу и в целом по предприятию.

 

I отдел	II отдел
Зарплата (руб.)	Число работников (чел.)	Зарплата (руб.)	Число работников (чел.)

 

Задача №11.Имеются данные о посевной площади и урожайности пшеницы:

 

№ бригады	Посевная площадь (га)	Урожайность (ц/га)

 

Определить:

1) среднюю урожайность пшеницы;

2) среднюю посевную площадь;

3) средний валовой сбор пшеницы.

 

Задача №12. По данным таблицы о продаже мяса торговым предприятием, руб :

Наименование мяса	I квартал	II квартал
Цена	Выручка	Цена	Выручка
Свинина
Говядина

 

Вычислить:

1) среднюю цену за 1 кг мяса в каждом квартале;

2) изменение средней цены во II квартале по сравнению с I кварталом в абсолютных и относительных величинах.

 

Задача №13. По данным таблицы о прибыли предприятия:

 

Квартал	I	II	III	IV
Прибыль (тыс. руб.)

 

Вычислить:

1) средний уровень прибыли за год;

2) абсолютный прирост, темп роста, темп прироста и абсолютное значение 1% прироста прибыли базисным способом.

Задача №14. Вычислить средний уровень оборотных средств за квартал; абсолютный прирост, темп роста, темп прироста и абсолютное значение 1% прироста оборотных средств предприятия цепным способом:

 

	на 1января	на 1 февраля	на 1марта	на 1апреля
Остатки оборотных средств (тыс. руб.)	1260,4	1300,2	1289,7	1500,0

Задача №15. Вычислить по данным таблицы средние показатели ряда динамики: средний уровень, средний абсолютный прирост, средний темп роста и прироста.

Год
Издержки обращения (тыс. руб.)	730,5	813,4	800,0	790,3

 

Задача №16. Задолженность предприятия банку по ссудам составила, тыс. руб.: на 1 марта – 110; на 10 марта – 85; на 23 марта – 30.

Вычислить средний размер задолженности по ссудам за март месяц.

 

Задача № 17. Поданным таблицы:

 

Товарные группы	Цена (руб.)	Количество проданной продукции
I квартал	II квартал	I квартал	II квартал
А
Б

 

Вычислить:

1) индивидуальные индексы физического объёма продажи товаров и цены;

2) общие индексы физического объёма товарооборота, цены и товарооборота в фактических ценах.

 

Задача № 18. В отчётном периоде по сравнению с базисным периодом товарооборот в фактических ценах возрос на 14%, а физический объём товарооборота снизился на 3,2%.Вычислить индекс изменения цен.

 

Задача № 19. Товарооборот в фактических ценах возрос в отчётном периоде по сравнению с базисным периодом на 3,1%, а цены на реализованные товары увеличились на 15%.

Вычислить индекс физического объёма товарооборота.

Задача № 20. На основании данных таблицы вычислить общий индекс физического объёма товарооборота:

 

Товарные группы	Товарооборот базисного периода (тыс. руб.)	Изменение количества проданного товара (%)
А Б		+ 5,4 – 2,6

Задача № 21. На основании данных таблицы вычислить общий индекс цены:

 

Товарные группы	Товарооборот отчётного периода (тыс. руб.)	Изменение цен (%)
А Б В		+ 6,5 – 1,9 + 12,0

 

Задача № 22.Вычислить коэффициент эластичности спроса, если товарооборот универмага в первом полугодии составил 4562 тыс. руб., а во втором полугодии – 5790 тыс. руб.; средний индекс цен – 1,129.

 

Задача № 23.Определить индекс покупательной способности рубля, если в отчётном периоде расходы населения составили:

а) на покупку товаров – 634 млн. руб.;

б) на оплату услуг – 510 млн. руб.

Цены по сравнению с базисным периодом увеличились:

а) на товары – 10,5%;

б) на услуги – 8,2%.

 

Задача №24.Вычислить общие индексы физического объёма товарооборота, цены и товарооборота в фактических ценах по следующим данным, тыс. руб.:

1) сумма стоимости продажи товаров в отчётном периоде

в ценах базисного периода – 1055;

2) сумма стоимости продажи товаров в базисном периоде

в ценах базисного периода – 985;

3) сумма стоимости продажи товаров в отчётном периоде

в ценах отчётного периода – 1300.

Выразить взаимосвязь индексов в абсолютных величинах.

 

Задача №25.Определить среднееизменение цен, если товарооборот базисного периода составил 1350 тыс. руб., товарооборот отчётного периода составил 1670 тыс. руб. и общий индекс физического объёма товарооборота – 1,136