 |
Главная |
Раскрытие неопределённостей от показательных и логарифмических функций
|
из
5.00
|
Для функций этого третьего класса также требуется специальная Теорема (второй замечательный предел). 
где число 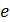 - бесконечная, непериодическая десятичная дробь
- бесконечная, непериодическая десятичная дробь  (посмотрите приближённое значение этого числа на своём калькуляторе). Обычно помнят
(посмотрите приближённое значение этого числа на своём калькуляторе). Обычно помнят  . Важно, что
. Важно, что  Заметим, что число
Заметим, что число 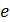 , пожалуй, самое употребительное число и, соответственнно, связанные с этим числом функции
, пожалуй, самое употребительное число и, соответственнно, связанные с этим числом функции 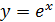 и
и  натуральные лагорифмы. График функции
натуральные лагорифмы. График функции 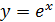 называется экспонентой.
называется экспонентой.
Теорему принимаем без доказательства и заметим, что теорема раскрывает неопределённость типа 




 3
3


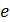

|


 1
1

| |
|
| |
| |

 0 x Рис.2
0 x Рис.2
Пример 25. Вычислить 
Решение. Сделаем замену переменной  тогда
тогда  и получим
и получим 
Заметим, что второй замечательный предел применяется общем виде:
Пусть  , где
, где  - любое число или
- любое число или  , но функция
, но функция  , тогда
, тогда
 (1)
(1)
Пример 26. Вычислить 
Решение. Посмотрим на структуру формулы (1): во – первых, в основании степени находится сумма единицы и некоторой б.м. функции  ; во – вторых, в показателе степени стоит
; во – вторых, в показателе степени стоит  - выражение, обратное второму слагаемому в основании степени («перевёрнутое» второе слагаемое),
- выражение, обратное второму слагаемому в основании степени («перевёрнутое» второе слагаемое),
Таким образом, задача ясна: надо выделить слагаемое  Это можно делать различными искусственными методами, но проще всего следующим образом – добавим и отнимем единицу в основании степени:
Это можно делать различными искусственными методами, но проще всего следующим образом – добавим и отнимем единицу в основании степени:


Вот мы и получили функцию  – она является б.м. при
– она является б.м. при  . Далее надо «подогнать» наш предел под форму второго замечательного предела, т.е. под формулу (1). Это означает, что в показателе степени надо иметь
. Далее надо «подогнать» наш предел под форму второго замечательного предела, т.е. под формулу (1). Это означает, что в показателе степени надо иметь  , т.е.
, т.е. 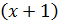 . Опять же проще всего просто поместить нужное выражение в показателе степени, а чтобы сохранить равенство, на это выражение надо поделить (в показателе степени):
. Опять же проще всего просто поместить нужное выражение в показателе степени, а чтобы сохранить равенство, на это выражение надо поделить (в показателе степени):


Пример хорошо показывает, что мы просто «подгоняли» под формулу (1). Ещё раз продемонстрируем это на следующих примерах.
Пример 27. 



Пример 28. 


Пример 29. 
Из второго замечательного предела в качестве следствия тоже можно получить цепочку эквивалентностей. Рассмотрим второй замечательный предел  и прологарифмируем обе части этого равенства по основанию е (говорят «возьмём натуральные логарифмы от обеих частей равенства»); при этом учтём, чтo логарифм степени равен показателю степени, умноженному на логарифм основания:
и прологарифмируем обе части этого равенства по основанию е (говорят «возьмём натуральные логарифмы от обеих частей равенства»); при этом учтём, чтo логарифм степени равен показателю степени, умноженному на логарифм основания:
 .
.
и окончательно получаем 
Следствие.  при
при  .
.
Пример 30. 
Следствие. 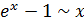 при
при 
Объединяя оба следствия, получим цепочку эквивалентностей  при
при  , или в общем виде
, или в общем виде
 при
при 
Пример 31. 
Цепочку эквивалентностей можно применить и для решения предыдущих примеров. Вернёмся к примеру 27 и обозначим его: А=  . Прологарифмируем это равенство:
. Прологарифмируем это равенство:

 lnA=
lnA=  )=
)=  - 1)=
- 1)=  )= ln(1+
)= ln(1+  )
)  =
=  =
=  lnA=
lnA=  , A=
, A=  .
.
|
из
5.00
|
Обсуждение в статье: Раскрытие неопределённостей от показательных и логарифмических функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы


