Основные идеи метода конечных элементов

Содержание

Введение.................................................................................................................................... 3

1 Идея и область применения метода конечных элементов............. 4

2 Основные идеи метода конечных элементов......................................... 31

3 Программный комплекс «ANSYS»........................................................................ 34

3.1 Структура программного комплекса «ANSYS»............................... 34

3.1.1 Модуль Preprocessor.................................................................................... 35

3.1.2 Модуль Solution................................................................................................. 36

3.1.3 Модуль General Postproc.......................................................................... 36

4 Разработка конечно-элементной модели боковой рамы тележки модели 18-100 37

4.1 Запуск программы «ANSYS» и указание имени задачи............ 38

4.2 Работа с модулем Preprocessor........................................................... 40

4.3 Работа с модулем Solution........................................................................ 71

4.4 Работа с модулем General Postproc................................................. 75

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.......................................................... 79

 

Введение

В процессе проектирования нового и модернизации существующего подвижного состава большое внимание уделяется оценке прочности вагонных конструкций с целью безусловного обеспечения требований безопасности при перевозке пассажиров и грузов железнодорожным транспортом.

Большинство современных методов проектирования базируются на использовании метода конечных элементов (МКЭ), позволяющего эффективно оценивать нагруженность отдельных элементов, узлов и всего вагона в целом, проводить локализацию зон концентрации напряжений и, в конечном итоге, улучшать технико-экономические показатели вагона. На базе МКЭ также может быть получена информация для прогнозирования долговечности вагонов и установления условий их безопасной эксплуатации.

Грамотный инженерный подход к использованию МКЭ позволяет существенно сократить трудозатраты на проектирование нового и модернизацию существующего подвижного состава.

Целью учебного пособия является изложение основ МКЭ и реализующего его программного комплекса, необходимых для практической работы по оценке прочности вагонных конструкций на современных ЭВМ.

Идея и область применения метода конечных

Элементов

Основные понятия

Возникновение МКЭ связано с решением задач космических исследований (1950 г.). Этот метод возникиз строительной механики и теории упругости, а уже потом был осмыслен математиками, которые часто называют данный метод вариационно-разностным, подчеркивая тем самым его математическую природу. Они занимаются математическим обоснованием МКЭ, т. е. проводят теоретический анализ его сходимости и точности результатов. Представители же инженерного направления решают довольно сложные технические задачи, часто не задумываясь над строгим обоснованием применяемых ими приемов, а построенные алгоритмы и программы проверяют на известных точных решениях.

Существенный толчок в своем развитии МКЭ получил после того, как было доказано (1963 г.), что этот метод можно рассматривать как один из вариантов известного в строительной механике метода Рэлея—Ритца, который путем минимизации потенциальной энергии позволяет свести задачу к системе линейных уравнений равновесия.

Связь МКЭ с процедурой минимизации позволила широко использовать его при решении задач в других областях техники. Метод применялся к задачам, описываемым уравнениями Лапласа или Пуассона (например, электромагнитные поля). Решение этих уравнений также связано с минимизацией некоторого функционала. Известны решения с помощью этого метода задач распространения тепла, задач гидромеханики и, в частности, задач о течении жидкости в пористой среде.

Область применения МКЭ существенно расширилась, когда было показано (1968 г.), что уравнения, определяющие элементы в задачах строительной механики, распространения тепла, гидромеханики, могут быть легко получены с помощью таких вариантов метода взвешенных невязок, как метод Галёркина или способ наименьших квадратов. Установление этого факта сыграло важную роль в теоретическом обосновании МКЭ, т. к. позволило применять его при решении многих типов дифференциальных уравнений. Таким образом, метод конечных элементов из численной процедуры решения задач строительной механики превратился в общий метод численного решения дифференциальных уравнений или систем дифференциальных уравнений. Этот прогресс был достигнут за довольно короткий срок, благодаря совершенствованию быстродействующих ЭВМ.

Более подробно история возникновения и прикладная теории МКЭ изложены в работах [1-6].

Кратко изложим сущность МКЭ и основные этапы его практической реализации.

Основная идея метода конечных элементов состоит в том, что любую непрерывную величину (перемещение, температура, давление и т. п.) можно аппроксимировать моделью, состоящей из отдельных элементов (участков). На каждом из отдельных элементов исследуемая непрерывная величина аппроксимируется кусочно-непрерывной функцией, которая строится на значениях исследуемой непрерывной величины в конечном числе точек рассматриваемого элемента.

В общем случае непрерывная величина заранее неизвестна, и нужно определить значения этой величины в некоторых внутренних точках области. Дискретную модель, однако, очень легко построить, если сначала предположить, что известны числовые значения этой величины в некоторых внутренних точках области (в дальнейшем эти точки мы назовем «узлами»). После этого можно перейти к общему случаю.

Чаще всего при построении дискретной модели непрерывной величины поступают следующим образом:

1. Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

2. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками или просто узлами.

3. Значение непрерывной величины в каждой узловой точке первоначально считается известным, однако необходимо помнить, что эти значения в действительности еще предстоит определить путем наложения на них дополнительных ограничений в зависимости от физической сущности задачи.

4. Используя значения исследуемой непрерывной величины в узловых точках и ту или иную аппроксимирующую функцию, определяют значение исследуемой величины внутри области.

Поясним сказанное выше на примере исследования распределения температуры в стержне. В общем случае распределение температуры неизвестно, и мы хотим определить значения этой величины в некоторых точках. Методика построения дискретной модели остается точно такой же, как описано выше, но с добавлением одного дополнительного шага. Первоначально считают значения температуры в некоторых точках в пределах стержня известными. Определяют множество узлов и значения температуры в этих узлах, которые теперь являются переменными, т. к. они заранее неизвестны. Область (в нашем случае – длина стержня) разбивается на элементы, для каждого из которых определяется аппроксимирующая функция. Узловые значения температуры должны быть теперь «выбраны» таким образом, чтобы с учетом граничных условий (например, значений температуры на концах стержня) обеспечить наилучшее приближение к истинному распределению температуры вдоль стержня. Этот «выбор» осуществляется путем минимизации некоторой величины, связанной с физической сущностью задачи. Если рассматривается задача распространения тепла, то минимизируется функция, связанная с соответствующим дифференциальным уравнением. Процесс минимизации сводится к решению систем линейных алгебраических уравнений относительно узловых значений температуры. В прочностных задачах, где определяются поля перемещений, деформаций и напряжений, минимизируется потенциальная энергия деформированного тела.

Аппроксимирующие функции чаще всего выбираются в виде линейных, квадратичных или кубических полиномов. Для каждого элемента можно подбирать свой полином, но полиномы подбираются таким образом, чтобы сохранить непрерывность величины вдоль границ элемента. Этот полином, связанный с данным элементом, называют «функцией элемента».

С этой точки зрения конструкцию можно рассматривать как некоторую совокупность конструкционных элементов, соединенных в конечном числе узловых точек. Если известны соотношения между силами и перемещениями для каждого отдельного элемента, то, используя известные приемы строительной механики, можно описать свойства и исследовать поведение конструкции в целом.

В сплошной среде число точек связи бесконечно, и именно это составляет основную трудность получения численных решений в теории упругости. Понятие «конечных элементов» представляет собой попытку преодолеть эту трудность путем разбиения сплошного тела на отдельные элементы, взаимодействующие между собой только в узловых точках, в которых вводятся фиктивные силы, эквивалентные поверхностным напряжениям, распределенным по границам элементов. Если такая идеализация допустима, то задача сводится к обычной задаче строительной механики, которая может быть решена численно.

Таким образом, при использовании МКЭ решение краевой задачи для заданной области ищется в виде набора функций, определенных на некоторых подобластях (конечных элементах).

 

1.1 Основные этапы практической реализации

Как было отмечено ранее, согласно МКЭ, модель конструкции сложной формы подразделяется на более мелкие части (конечные элементы) сравнительно простой формы, в пределах которых ищется приближенное решение. Результатом такого моделирования обычно является поле напряжений и смещений в целой конструкции.

Таким образом, решение задачи с применением МКЭ состоит из следующих основных этапов (рисунок 1):

Рисунок 1 – Этапы решения задач с применением МКЭ

1) идентификация задачи, присвоение ей имени; создание чертежа конструкции и нагрузок; 2) создание геометрии модели, пригодной для МКЭ; 3) разбиение модели на сетку конечных элементов; 4) приложение к модели граничных условий (закрепление на границе или граничные нагрузки); 5) численное решение системы уравнений (автоматически); 6) анализ результатов.

Этапы 1, 2, 3, 4 относятся к препроцессорной стадии, этап 5 – к процессорной стадии, этап 6 – к постпроцессорной стадии.

Построенная модель делится на конечные элементы достаточно простой формы. Имеются несколько типичных форм конечных элементов, в которых поле смещений определяется по смещениям узлов с помощью некоторых интерполяционных функций. По вычисленным таким образом смещениям определяются поля напряжений и деформаций.

Наиболее трудоемкий этап решения задач с помощью МКЭ — это создание конечно-элементной модели на стадии препроцеcсорной подготовки (preprocessor), т. к. автоматическое построение сетки элементов не гарантирует от появления ошибок. Правильное приложение нагрузок и граничных условий также представляет определенные трудности.

Пятый из перечисленных выше этапов (численное решение системы уравнений) выполняется автоматически и, как правило, особых трудностей не вызывает (за исключением систем с плохо обусловленной матрицей жесткости).

Шестой этап (анализ результатов) существенно облегчается имеющимися мощными инструментальными средствами визуализации результатов.

 

 

Рисунок 2 – Разбивка конструкции на КЭ

Учитывая то, что в конечно-элементных задачах неизвестными являются перемещения в узлах, а также то, что в трехмерных задачах каждый узел тетрагонального элемента может иметь перемещения по трем направлениям (Рисунок2), система уравнений равновесия, записанная в матричной форме, может иметь размерность, достигающую 100000 и более. Однако для современных ЭВМ решение таких систем уравнений – вполне посильная задача. При составлении уравнений равновесия учитывается, что сумма проекций всех сил на каждую из координатных осей равна нулю, а сумма внутренних сил равна внешней силе с обратным знаком.

В трехмерных моделях число узлов обычно больше числа элементов, а число степеней свободы в 3 раза больше числа узлов (за исключением числа кинематических граничных условий).

Матрица жесткости [К] связывает векторы узловых смещений {U} и нагрузок {Р}.

Матрица жесткости является симметричной диагональной матрицей, что существенно облегчает ее обработку.

1.2 Конечные элементы

Как следует из основной концепции МКЭ, вся модель конструкции (или отдельной ее части) делится на множество конечных элементов, соединенных между собой в вершинах (узлах) (Рисунок 3). Силы действуют в узлах. Конечный элемент не является «абсолютно жестким» телом.

 

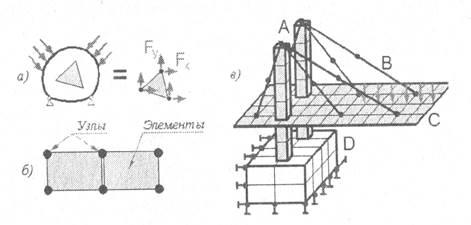
Рисунок 3 – Конечные элементы

Конечно-элементная модель предполагает, что напряжения и деформации имеются и вне данного конечного элемента. Имеются несколько наиболее употребительных типов конечных элементов (Рисунок 3): брус (А), стержень (В), тонкая пластина или оболочка (С), двумерное или трехмерное тело (О). Естественно, что при построении модели могут быть использованы не один, а несколько типов элементов.

Достоверность расчетов по МКЭ зависит от многих факторов, в том числе и от количества конечных элементов. Однако, если напряжения не меняются значительно в пределах модели, то количество конечных элементов несущественно влияет на точность вычисления напряжений.

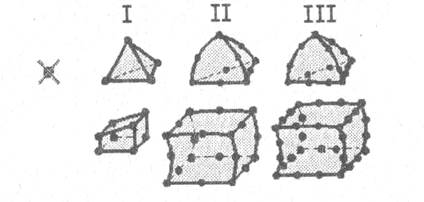
Рисунок 4 – Типы конечных элементов

 

Конечные элементы могут быть линейными (элементы первого порядка) или параболическими (элементы второго порядка) (Рисунок 4). Линейные элементы имеют прямые стороны и узлы только в углах. Таким образом, минимальное число узлов трехмерного элемента равно 4. Параболические элементы могут иметь промежуточный узел вдоль каждой из сторон.

Именно благодаря этому стороны элемента могут быть криволинейными (параболическими). При равном количестве элементов параболические элементы дают большую точность вычислений, т. к. они более точно воспроизводят криволинейную геометрию модели и имеют более точные функции формы (аппроксимирующие функции). Однако расчет с применением конечных элементов высоких порядков требует больших компьютерных ресурсов и большего машинного времени.

Рассмотрим самый простой трехмерный линейный элемент с 8 узлами (Рисунок 5). Каждый из узлов имеет 3 степени свободы. Это означает, что необходимо рассмотреть 24 узловые смещения и столько же узловых сил. Таким образом, размерность матрицы жесткости [К], связывающей вектор узловых смещений с вектором узловых сил, будет [24 х 24].

Компоненты матрицы жесткости прямо пропорциональны модулю упругости. Таким образом, нулевой модуль упругости означает отсутствие конечного элемента (Рисунок 6). В этом случае деление на нулевой модуль упругости приведет к значительным погрешностям.

Бесконечно большой модуль упругости означает, что данный элемент является абсолютно жестким. Кроме того, если теория упругости допускает бесконечные напряжения (например, в вершине трещины), то в МКЭ напряжения всегда конечны.

Рисунок 5 – Матрица жесткости трехмерного элемента с 8 узлами

Рисунок 6 – Пример отсутствия КЭ

Несколько замечаний относительно соотношения между сторонами элемента. «Длинные» элементы с соотношением сторон 2 и более (Рисунок 7) можно использовать, если не ожидаются большие градиенты смещений, деформаций и напряжений, т. е. вдали от зоны действия концентраторов напряжений.

Рисунок 7 – Соотношения длин КЭ

Если конструкция и нагрузки симметричны относительно оси, смотри Рисунок 8, задача может быть решена с помощью плоских симметричных конечных элементов.

 

Рисунок 8 – Симметричные нагрузки

 

Построение сетки конечных элементов

Одним из наиболее важных этапов в конечно-элементном анализе является построение на модели сетки из конечных элементов, т. е. разделение всей модели на маленькие кусочки (конечные элементы), связанные между собой в узлах.

В программном комплексе ANSYS имеется два основных метода построения сетки: построение произвольной сетки (рисунок 9а) и построение упорядоченной сетки (Рис. 9б). Произвольная сетка строится автоматически, при этом соседние элементы могут существенно отличаться по размерам (Рис. 9а). Упорядоченная сетка строится путем деления геометрических элементов модели на некоторое число частей (рис.9 б). В автоматически построенных сетках с большим числом элементов число узлов преобладает над числом элементов. Отношение между узлами и элементами, примерно, 2:1 для плоских произвольных сеток и 6:1 для произвольных трехмерных сеток с четырехгранными элементами.

 

 

Рисунок 9 – Методы построения сетки в программе «ANSYS»

а) построение произвольной сетки; б) построение упорядоченной сетки

Рисунок 10 – Зависимость количества КЭ от размеров элемента

Рисунок 11 – Рекомендации по разбивке конструкции на КЭ

Очевидно, что чем меньше линейный размер конечного элемента А (Рисунок 10), тем большее количество элементов в модели, при этом время вычислений существенно возрастает, а ошибки анализа уменьшаются. Однако, ошибки уменьшаются не до нуля, т. к. с увеличением числа элементов накапливаются ошибки округления в ЭВМ.

Практика расчетов с применением МКЭ позволяет дать следующие рекомендации (Рисунок 11):

1) линейные элементы требуют более частой сетки, чем квадратичные элементы (с одним промежуточным узлом) или кубичные (с двумя промежуточными узлами);

2) упорядоченная сетка (б) является более предпочтительной, чем произвольная сетка (а);

3) прямоугольная сетка с 4 узлами (в) более предпочтительна, чем сетка с треугольными элементами (б);

4) сетка треугольных элементов с промежуточными узлами (г) имеет, по крайней мере, ту же самую точность, что и сетка прямоугольных элементов с 4 узлами (в);

5) прямоугольная сетка с 8 узлами (д) является более предпочтительной, чем сетка треугольных элементов с промежуточными узлами (г), несмотря на больший размер прямоугольных элементов; 6) аппроксимация смещений кубическим полиномом (е) не требует более мелкой сетки.

Необходимо помнить, что МКЭ — приближенный метод, точность которого зависит от правильного выбора типов и размеров конечных элементов. Так, например, более частая сетка требуется там, где ожидается большой градиент деформаций или напряжений (Рис. 12).

В то же время более редкая сетка может применяться в зонах с более или менее постоянными деформациями или напряжениями, а также в областях, не представляющих особого интереса. В связи с этим исследователь должен уметь предвидеть области концентрации напряжений.

 

 

Рисунок 12 – Сетка КЭ в зоне высокого градиента напряжений

 

 

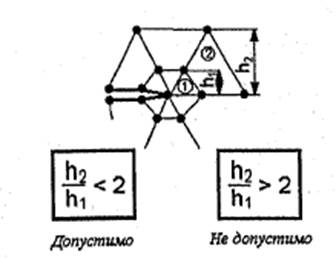
Рисунок 13 – Правило разбивки сетки КЭ в зоне высокого градиента

напряжений

Необходимо заметить, что точность результатов анализа уменьшается, если размеры соседних элементов вблизи концентратора напряжений существенно различны (Рисунок 13).

Форма конечных элементов также влияет на точность вычислений. С этой точки зрения следует избегать слишком узких и вытянутых элементов (Рисунок 14), т. к. элементы с одинаковыми, примерно, сторонами дают меньшую ошибку.

 

Удачно Неудачно

Рисунок 14 – Примеры формы КЭ

 

Дополнительные сведения об ошибках, связанных с расположением, формой и размерами КЭ, приведены в п. 1.4 «Точность результатов».

Одновременно в сетке могут присутствовать треугольные и четырехугольные элементы, однако между ними не должно быть разрывов (Рисунок 15).

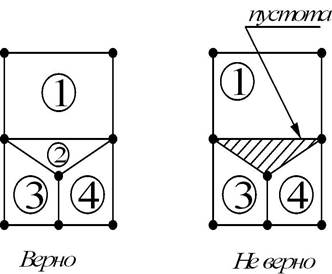
Рисунок 15 – Сетка КЭ

Для дальнейшего объединения элементов в сетку узлы последовательно нумеруются. Запрещается строить четырехугольные элементы с углами, больше 180°.

 

Рисунок 16 – Примеры КЭ.

 

1.3 Граничные условия

Задание граничных условий – один из ответственных этапов конечно-элементного анализа. Так, например, на модели (Рисунок 17), изображенные графические граничные условия в узлах А и В служат для того, чтобы перемещение указанных узлов модели соответствовали перемещениям тех же узлов натурной конструкции с учетом наложенных на них связями ограничений. При этом перемещения могут приобретать как нулевые (в узле А), так и не нулевые (в узде В) значения. Существуют также граничные условия, при которых задаются нагрузки (узел С).

 

Рисунок 17 – Граничные условия

Рисунок 18 – Приложение граничных условий

 

Граничные условия (перемещения или силы) прикладываются только к узлам (Рисунок 18). Максимальное число граничных условий, приложенных в узле, равно числу его степеней свободы – 3 силы или 3 перемещения.

Необходимо обратить особое внимание на то, что число граничных условий должно быть минимально необходимым (не меньше и не больше). Так, например, не следует фиксировать все степени свободы (все перемещения) в каждом узле элемента (Рисунок 19 а); не следует также прикладывать силу в узле в том же самом направлении, в котором в данном узле зафиксировано смещение (Рисунок 19 б); полное отсутствие закрепления вдоль какой-либо из осей (Рисунок 19 в) может привести при анализе к кажущемуся сдвигу вдоль этой оси вследствие неизбежных ошибок округления при численных расчетах. Для рассмотренных примеров правильные схемы граничных условий смотри Рисунок 19 (г, д).

Рисунок 19 – Число граничных условий

Схема размещения граничных условий зависит от вида нагружения (растяжение, чистый изгиб, сдвиг), смотри Рисунок 20.

 

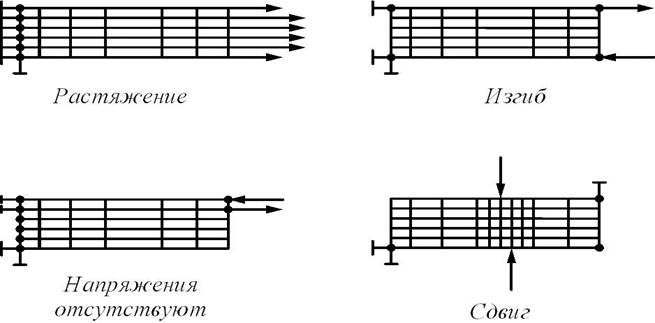
Рисунок 20 – Схема размещения граничных условий

Если конструкция имеет оси или плоскости симметрии, то при назначении граничных условий необходимо это учитывать. Так, например, пресс с жесткими пуансонами, сжимающий куб из более мягкого однородного материала (Рисунок 21), имеет три плоскости симметрии. Очевидно, в этом случае нет необходимости моделировать всю конструкцию целиком.

Рисунок 21 – Пресс с жесткими пуансонами

Можно смоделировать только часть конструкции (1/4 или 1/8), имея в виду, что в точках на плоскостях симметрии соответствующие перемещения равны нулю. Это обстоятельство мы учитываем соответствующими граничными условиями в узлах элементов, лежащих на плоскостях симметрии (Рисунок 21б).

Выбор размеров элементов и граничных условий при построении сетки можно существенно упростить, если принять во внимание принцип Сен-Венана: две статически эквивалентные системы сил создают одно и тоже поле напряжений на расстоянии от их точек приложения, больше, чем характерный линейный размер поперечного сечения (b>a, Рисунок 22).

Рисунок 22 – Принцип Сен-Венана

Рассмотрим следующую ситуацию. Известно, что чрезмерно большие растягивающие напряжения являются основной причиной многих разрушений. В этом случае, если зона максимальных растягивающих напряжений находится вдали от точки приложения силы (например, как на схеме Рисунок 23), нет

 

Рисунок 23 – Расчетный случай

необходимости строить подробную сетку элементов вблизи этой точки, т.к. здесь действуют, в основном, сжимающие напряжения.

1.4 Точность результатов

Численный анализ, к которому относится и МКЭ, требует некоторой идеализации реальной конструкции. Поэтому, несмотря на мощное развитие вычислительной техники, результаты вычислений по МКЭ не свободны от ошибок. Использование вычислительной техники в роли «черного ящика», без понимания основных процессов и этапов вычислений, может привести к существенным ошибкам. К сожалению, не исключены также и ошибки операторов.

Приступая к конечно-элементному анализу, инженер должен понять:

­ К какой области анализа относится данная задача;

­ Какая часть всей конструкции должна исследоваться подробнее;

­ Какие упрощения можно допустить в данной задаче.

Естественно, это требует определенной квалификации исследователя.

Ошибки могут возникать на различных стадиях конечно-элементного анализа: при постановке задачи, дискретизации (построении модели), численном решении.

Ошибки постановки задачи могут возникать, когда выбранный тип конечных элементов или их размер не соответствует физическому поведению материала в конструкции. Несколько уменьшить эту ошибку (по крайней мере, ту ее часть, которая связана с размером конечного элемента) можно, используя автоматическое построение сетки. Однако основным источником ошибок при постановке задачи является некорректное задание граничных условий. Таким образом, успех конечно-элементного анализа зависит от точности воспроизведения на модели граничных условий, геометрии и свойств материала натурной конструкции.

Ошибки дискретизации возникают при замене реальной конструкции ограниченным числом конечных элементов (с учетом их формы и размеров).

Ошибки, связанные с численным решением систем уравнений, обычно менее значимы, чем перечисленные выше два типа ошибок.

При конечно-элементном анализе, как правило, неизвестными являются смещения, и результатом решения в этом случае будет вектор смещений в узле . Смещения в других точках элемента вычисляются интерполяцией.

После аппроксимации поля смещений (в пределах элемента) соответствующим полиномом, называемым «функцией формы», могут быть вычислены деформации и напряжения. Описанная схема вычислений показывает, что наибольшая точность достигается при определении смещений в узлах.

Деформации вычисляются дифференцированием соответствующих смещений, поэтому максимальная точность вычислений деформаций и напряжений будет в центре элемента. На рисунке 24 показана деформированная частица для случая чистого изгиба.

Рисунок 24 – Деформированная частица для случая чистого изгиба

Как видим, теоретическое и численное решение совпадает в центральной части конечного элемента.

Тип и количество элементов влияют на точность вычислений. Так, например, при вычислении силы в случае нелинейного анализа, при небольшом числе конечных элементов их количество существенно влияет на величину вычисляемой силы (Рисунок 25). Однако при увеличении числа элементов результаты стабилизируются.

 

 

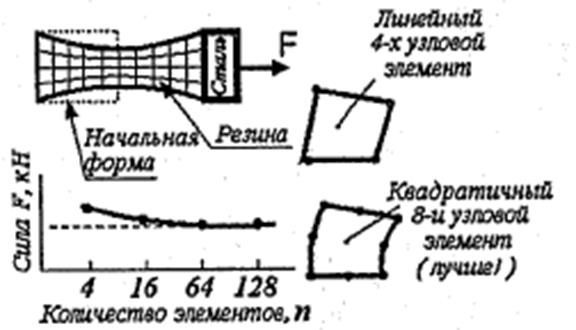
Рисунок 25 – Зависимость типа КЭ от величины вычисляемой силы

Существует два метода конечно-элементного анализа: h-метод (h – длина стороны КЭ) и р-метод (р – порядок полинома аппроксимирующей функции). Для повышения точности решения h-метод требует увеличения числа элементов. В соответствии с р-методом для увеличения точности надо повысить порядок полинома аппроксимирующей функции. Так, например, на рисунке 26 элементы более высокого порядка демонстрируют и большую точность результатов по сравнению с линейными элементами (Рисунок 26 а).

 

Рисунок 26 – Зависимость результата от количества числа элементов

На точность результатов влияет также и ориентация сторон элементов. Для изгибаемой консольной балки увеличение числа элементов по высоте балки не дает повышения точности результатов (Рисунок 26 в). Гораздо лучшие результаты дает увеличение числа элементов второго порядка по длине балки (Рисунок 26 г).

Для получения достоверных результатов в зонах концентрации напряжений размер элементов должен быть меньше. На рисунке 27 показан фрагмент растягиваемой полосы с центральным отверстием. Известно, что максимальные напряжения действуют в сечении А-А, поэтому в окрестности данного сечения сетка элементов должна быть гуще, чем у левой границы полосы.

 

 

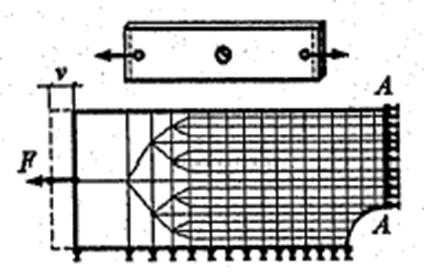
Рисунок 27 – Фрагмент растягиваемой полосы с центральным отверстием

1.5 Пример. Растяжение ступенчатого стержня

Поясним основные понятия МКЭ на простейшем примере осевого растяжения ступенчатого стержня. Данный пример сейчас будет приведен лишь в качестве иллюстрации, без подробных объяснений.

 

 

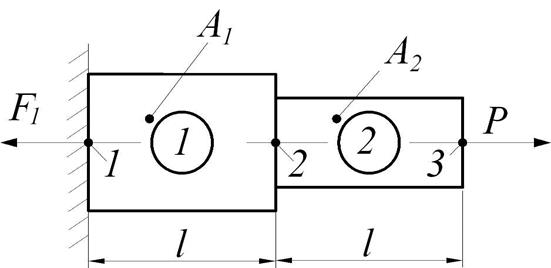
Рисунок 28 – Ступенчатый стержень

 

Ступенчатый стержень (Рисунок 28) с двумя ступенями одинаковой длины l и площадью поперечного сечения ступеней А₁ и А₂ жестко заделан с левого торца и нагружен на противоположном торце осевым усилием Р. Определить перемещения сечений 1, 2 и 3.

Разобьем стержень на два элемента (участка) 1, 2 и введем на границах элементов узлы 1, 2, 3, в которых будем отыскивать неизвестные перемещения u. Таким образом, ступенчатый стержень будем моделировать двумя последовательно соединенными стержневыми конечными элементами.

Рассмотрим отдельно стержневой элемент, изображенный на рисунке 29.

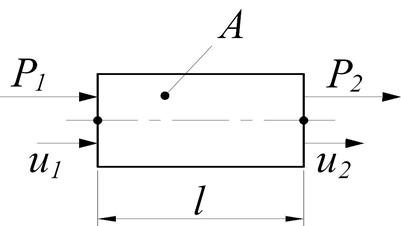
Рисунок 29 – Стержневой элемент

Он имеет длину l, площадь поперечного сечения А, в узлах приложены усилия Р₁ и Р₂, от которых эти узлы имеют осевые перемещения u₁ и u₂. Запишем для элемента на рисунке 29 соотношения, очевидные из курса сопротивления материалов:

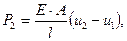, 1.1

или то же в матричной форме:

1.2

где Е – модуль упругости материала стержня.

Матрица , связывающая между собой в 1.2 узловые усилия и перемещения, носит название матрицы жесткости элемента.

Составим уравнение равновесия для всего стрежня, изображенного на рисунке 28, объединив соотношения для элементов 1 и 2, записанные с учетом (1.2). Так как стержень состоит из нескольких элементов, то естественно предположить, что матрица жесткости всего стержня должна включать в себя матрицы жесткости образующих его элементов. Для данной задачи главные диагонали матриц жесткости элементов должны совпадать с главной диагональю глобальной (общей) матрицы жесткости всего стержня и состыковываться в узле 2 (Рисунок 28).

На основании (1.2) общую систему уравнений равновесия можно записать в виде:

,

или

1.3

где u_i – перемещение i-го узла всей системы. В (1.3) учтено, что усилие Р приложено в узле 3, а усилие F₁ (реакция опоры) – в узле 1. Узел 2 свободен от внешних нагрузок.

Теперь следует наложить граничные условия в перемещениях, а именно: u₁=0. Это достигается замещением 1-й строки и 1-го столбца нулями и помещением на главную диагональ любого числа, отличного от нуля:

Решением этой системы линейных алгебраических уравнений является:

1.4

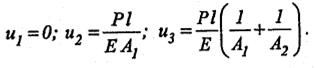
Основные идеи метода конечных элементов

Метод конечных элементов (МКЭ) – это способ анализа поведения реальной конструкции при заданных нагрузках и перемещениях. Основной единицей представления конструкции в этом анализе является конечный элемент (КЭ) – геометрически упрощенное представление малой части физической конструкции. Модель конструкции создается при помощи конечных элементов.

МКЭ – один из основных способов, применяемых для решения задач строительной механики, механики деформируемого твердого тела, теплопроводности, гидромеханики и др. Идея метода заключается в аппроксимации сплошной среды с бесконечным числом степеней свободы совокупностью простых элементов, имеющих конечное число степеней свободы и связанных между собой в узловых точках.

Для МКЭ характерны: широкий диапазон применимости, инвариантность по отношению к геометрии конструкции и механическим характеристикам материалов, простота учета взаимодействия конструкций с внешней средой (механические и температурные нагрузки, граничные условия и т.д.), высокая степень приспособленности к автоматизации всех этапов расчета. Популярность метода объясняется также простотой его физической интерпретации и очевидной связью с методами Ритца и перемещений, широко применяемыми в механике сплошных сред и строительной механике.

Основы МКЭ были разработаны различными специалистами - математиками, физиками и инженерами, а сам термин конечный элемент появился в статье Клаффа, посвященной решению плоской задачи теории упругости [1].

Конечные элементы (КЭ) объединяются в модель в некоторых точках пространства, называемых узлами. В этих точках элементы соединяются и движутся совместно. Узлы, которые пронумерованы для того, чтобы их можно было отличить друг от друга, вместе с элементами осуществляют приближенное геометрическое описание сложной модели. В зависимости от типа, ориентации и числа элементов, соединяющихся в узле, последний может противодействовать поступательным перемещениям и вращениям вдоль и относительно определенных направлений. Каждое отдельное возможное перемещение или вращение называется степенью свободы и представляет собой неизвестную величину, подлежащую определению. Таким образом, перемещение узла определяется его поступательными перемещениями вдоль глобальных осей координат X, У и Z и его вращениями относительно этих осей (т.е. узел может иметь всего 6 степеней свободы).

Созданная для расчета конечно-элементная модель – всего лишь приближенное представление реальной конструкции. Как во всех численных методах, расчет производится не для реальной конструкции, а для построенного упрощенного образа, т.е. модели. Таким образом, точность результатов конечно-элементного анализа зависит от качества разработанной модели.

В настоящее время возможности МКЭ значительно расширены [3] ‑ [5] что, несомненно, обусловлено появлением современных высокопроизводительных ЭВМ и программных комплексов, реализующих МКЭ.

Основное уравнение (система уравнений) МКЭ для решения задач статического нагружения имеет вид:

[К]*{d}={F}, (1)

где [К] – глобальная матрица жесткости исследуемой конструкции;

{F} – вектор приложенных статических нагрузок (сосредоточенных и распределенных);

{d} – вектор