Тема 5. Теория вероятностей

Тема1. Матрицы, определители и системы уравнений.

1. Определение матрицы

2. Единичная матрица

3. Треугольная матрица

4. Главная и побочная диагонали

5. Порядок(размер) матрицы

6. Равные матрицы

7. Транспонирование матрицы

8. Сложение матриц

9. Произведение матриц

10. Обратная матрица (алгоритм нахождения обратной матрицы)

11. Вычисление определителя методом треугольника

12. Вычисление определителя разложением по строке или столбцу

13. Минор

14. Алгебраическое дополнение

15. Решение систем методом Крамера

16. Решение систем методом Гаусса

17. Решение систем методом обратной матрицы

 

Образцы заданий:

1.

Найти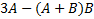

2.

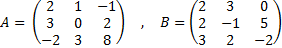
Найти: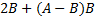

3. Транспонировать матрицу:

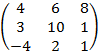
4. Найти обратную матрицу:

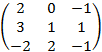
5. Вычислить определитель разложением по строке или столбцу:

А) 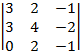б)

 

6. Вычислить определитель методом треугольника:

А) 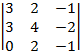б)

 

 

7. Решить систему методом Крамера:

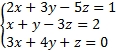
8. Решить систему методом Гаусса:

9. Решить систему методом обратной матрицы:

 

Тема 2. Интегрирование и дифференцирование:

 

1. Неопределенный интеграл

2. Интегрирование по частям

3. Формулы интегрирования

4. Формулы дифференцирования

5. Возрастание и убывание функции

6. Точки максимума и минимума

 

Задачи:

 

1. Найти производную:

а) у=7х²+4х³-6

b) у= 3sinx+4lnx-3e^x

c) y= 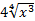-3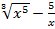

2. Исследовать функцию на возрастание и убывание, точки максимума и минимума.

а) у=х³-4х²

3. Найти вторую производную

а) у=6х⁷+2х⁴-6х

b) у=2cosx+3sinx-2lnx

c) y= +4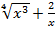

4. Вычислить интеграл:

а) 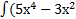+х-5)dx

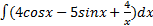b) b)

c)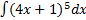

d)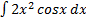

Тема 3. Дифференциальные уравнения.

Теоретические вопросы:

1. Понятие дифференциального уравнения

2. Понятие дифференциального уравнения с разделяющимися переменными

3. Понятие линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами

4. Задача Коши

Задачи:

1.

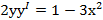
2. xdy

3.

4. y”+y’- 6y=0, y(0)=1, y’(0)=1

5. y”-6y’+45у=0

6. y”+2y’=0

7. y”+6y’+9у=0

8. y”-2y’-3y=0

9. y”-2y’+2y=0

10. y”+2y’-8y=0, y(0)=4, y’(0)= -4

Тема 4. Комбинаторика

Теоретические вопросы:

1. Понятие комбинаторики

2. Размещения

3. Перестановки

4. Сочетания

Задачи:

1. Сколько трехзначных чисел можно составить из 4 цифр: 1, 2, 3, 4?

2. Сколько четырехзначных чисел, в которых цифры не повторяются, можно составить из 4 цифр: 1, 2, 3, 4?

3. В семье 6 человек. За столом 6 стульев. В семье решили каждый вечер рассаживаться на эти 6 стульев по-новому. Сколько дней члены семьи смогут делать это без повторений?

4. Сколькими способами из класса, в котором учатся 30 школьников, можно выбрать капитана команды для математических соревнований и его заместителя?

5. Сколько трехкнопочных комбинаций существует на кодовом замке (все три кнопки нажимаются одновременно), если на нем всего 10 цифр?

6. У бармена есть 6 сортов зеленого чая. Для проведения чайной церемонии требуется подать зеленый чай ровно 3 различных сортов. Сколькими способами бармен может выполнить заказ?

7. Сколькими способами могут 6 человек стать в очередь к театральной кассе?

8. Сколькими способами можно расставить на полке семь книг, если две определенные книги должны всегда стоять рядом?

9. В группе из 20 девушек и 10 юношей. Сколько способами можно избрать двух девушек и трех юношей для участия в конференции.

Тема 5. Теория вероятностей.

Задачи:

1. В фирме такси в данный момент свободно 20 машин: 3 белых, 11 синих и 6 серых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет белое такси.

2. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 12 участников из России, в том числе Святослав Кружкин. Найдите вероятность того, что в первом туре Святослав Кружкин будет играть с каким-либо бадминтонистом из Рос‐ сии?

3. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Китая будет выступать после группы из Канады и после группы из Англии? Результат округлите до сотых.

4. За круглый стол на 101 стульев в случайном порядке рассаживаются 99 мальчиков и 2 девочки. Найдите вероятность того, что между двумя девочками будет сидеть один мальчик.

5. Люба включает телевизор. Телевизор включается на случайном канале. В это время по четырем каналам из шестнадцати показывают музыкальные клипы. Найдите вероятность того, что Люба попадет на канал, где клипы не идут.

6. На чемпионате по прыжкам в воду выступают 50 спортсменов, среди них 8 прыгунов из России и 10 прыгунов из Мексики. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что пятнадцатым будет выступать прыгун из России

7. В слу­чай­ном экс­пе­ри­мен­те бро­са­ют две иг­раль­ные кости. Най­ди­те ве­ро­ят­ность того, что в сумме вы­па­дет 8 очков. Ре­зуль­тат округ­ли­те до сотых.

8. В слу­чай­ном экс­пе­ри­мен­те сим­мет­рич­ную мо­не­ту бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что орел вы­па­дет ровно один раз.

9. Фаб­ри­ка вы­пус­ка­ет сумки. В сред­нем на 50 ка­че­ствен­ных сумок при­хо­дит­ся пять сумок со скры­ты­ми де­фек­та­ми. Най­ди­те ве­ро­ят­ность того, что куп­лен­ная сумка ока­жет­ся ка­че­ствен­ной. Ре­зуль­тат округ­ли­те до сотых.

10. На кла­ви­а­ту­ре те­ле­фо­на 10 цифр, от 0 до 9. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но на­жа­тая цифра будет чётной?