Сбалансированные по высоте деревья

В худшем случае, когда дерево вырождено в линейный список, хранение данных в упорядоченном бинарном дереве никакого выигрыша в сложности операций по сравнению с массивом или линейным списком не дает. В лучшем случае, когда дерево сбалансировано, для всех операций получается логарифмическая сложность, что гораздо лучше. Идеально сбалансированным называется дерево, у которого для каждой вершины выполняется требование: число вершин в левом и правом поддеревьях различается не более чем на 1.

Однако идеальную сбалансированность довольно трудно поддерживать. В некоторых случаях при добавлении или удалении элементов может потребоваться значительная перестройка дерева, не гарантирующая логарифмической сложности. В 1962 году два советских математика: Г.М. Адельсон-Вельский и Е.М. Ландис – ввели менее строгое определение сбалансированности и доказали, что при таком определении можно написать программы добавления и/или удаления, имеющие логарифмическую сложность и сохраняющие дерево сбалансированным. Дерево считается сбалансированным по АВЛ (сокращения от фамилий Г.М. Адельсон-Вельский и Е.М. Ландис), если для каждой вершины выполняется требование: высота левого и правого поддеревьев различаются не более, чем на 1. Не всякое сбалансированное по АВЛ дерево идеально сбалансировано, но всякое идеально сбалансированное дерево сбалансировано по АВЛ.

При операциях добавления и удаления может произойти нарушение сбалансированности дерева. В этом случае потребуются некоторые преобразования, не нарушающие упорядоченности дерева и способствующие лучшей сбалансированности.

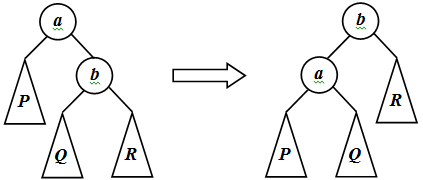
Рассмотрим такие преобразования. Пусть вершина a имеет правый потомок b. Обозначим через P левое поддерево вершины a, через Q и R – левое и правое поддеревья вершины b соответственно. Упорядоченность дерева требует, чтобы P<a<Q<b<R. Точно того же требует упорядоченность дерева с корнем b, его левым потомком a, в котором P и Q – левое и правое поддеревья вершины a, R – правое поддерево вершины b. Поэтому первое дерево можно преобразовать во второе, не нарушая упорядоченности. Такое преобразование называется малым правым вращением. Аналогично определяется симметричное ему малое левое вращение.

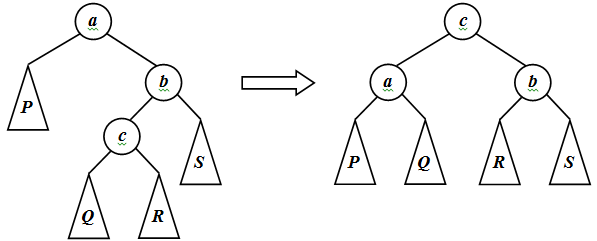
Пусть b – правый потомок вершины a, c – левый потомок вершины b, P – левое поддерево вершины a, Q и R – соответственно левое и правое поддеревья вершины c, S – правое поддерево b. Тогда P<a<Q<c<R<b<S. Такой же порядок соответствует дереву с корнем c, имеющим левый потомок a и правый потомок b, для которых P и Q – поддеревья вершины a, а R и S – поддеревья вершины b. Соответствующее преобразование будем называть большим правым вращением. Аналогично определяется симметричное ему большое левое вращение.

Схематично алгоритм добавления нового элемента в сбалансированное по АВЛ дерево будет состоять из следующих трех основных шагов.

Шаг 1. Поиск по дереву.

Шаг 2. Вставка элемента в место, где закончился поиск, если элемент отсутствует.

Шаг 3. Восстановление сбалансированности.

Первый шаг необходим для того, чтобы убедиться в отсутствии элемента в дереве, а также найти такое место вставки, чтобы после вставки дерево осталось упорядоченным. Третий шаг представляет собой обратный проход по пути поиска: от места добавления к корню дерева. По мере продвижения по этому пути корректируются показатели сбалансированности проходимых вершин, и производится балансировка там, где это необходимо. Добавление элемента в дерево никогда не требует более одного поворота.

Алгоритм удаления элемента из сбалансированного дерева будет выглядеть так:

Шаг 1. Поиск по дереву.

Шаг 2. Удаление элемента из дерева.

Шаг 3. Восстановление сбалансированности дерева (обратный проход).

Первый шаг необходим, чтобы найти в дереве вершину, которая должна быть удалена. Третий шаг представляет собой обратный проход от места, из которого взят элемент для замены удаляемого, или от места, из которого удален элемент, если в замене не было необходимости. Операция удаления может потребовать перебалансировки всех вершин вдоль обратного пути к корню дерева, т.е. порядка log n вершин. Таким образом, алгоритмы поиска, добавления и удаления элементов в сбалансированном по АВЛ дереве имеют сложность, пропорциональную O(log n).