Задача 2. Работа с графиками (Зайчиков Ю.)

Класс

Задача 1. Полет в облаках (Замятнин М.).

Облетая грозовую тучу, самолет, летящий на восток со скоростью υ₀ = 134 м/с, сделал несколько маневров. Сначала он в течение некоторого времени τ летел с ускорением a, направленным на юг, в результате чего его скорость выросла до υ₁= . Затем в течение времени τ он летел с таким же ускорением a, направленным на восток. И, наконец, на третьем участке пути, в течение времени τ он летел с ускорением 2a, направленным на север. Какой стала скорость самолета, и под каким углом к исходному курсу (на восток) она оказалась направлена после завершения маневрирования?

Возможное решение.При равноускоренном движении скорость самолёта . Направим ось X на восток, а ось Y – на север. Так как после первого маневра скорость самолёта возросла до υ₁= , то по теореме Пифагора

(1)

Решение задачи сводится к построению векторного многоугольника (рис. 1).

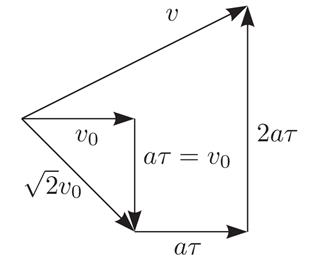
Рис. 1

После завершения маневров конечная скорость станет равна

. (2)

Модуль скорости равен

. (3)

Числовое значение

. (4)

Новый курс направлен на северо-восток под углом α к восточному направлению. Угол α найдём из условия:

, или . 2 балла

Критерии оценивания.

(1) Найдена проекция 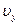скорости самолёта 1 балл

(2) Записано векторное уравнение для конечной скорости самолёта 3 балла

(3) Получено выражение для модуля конечной скорости 2 балла

(4) Получено числовое значение искомой скорости 1 балл

(5) Найдено направление вектора искомой скорости 3 балла

Задача 2. Работа с графиками (Зайчиков Ю.).

В модели железной дороги электровоз движется по прямолинейному пути. Зависимость координаты электровоза от времени приведена на рисунке. Начертите график зависимости скорости поезда от времени. Вычислите скорость поезда в точках А, Б, В, Г, Д. Найдите ускорение поезда на участках (А – Б), (Б – Г) и (Г – Д). Известно, что участки (А – Б), (Б – Г) и (Г – Д) – ветви парабол.

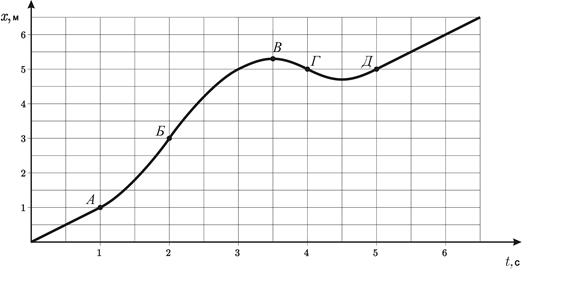
Рис. 2

Возможное решение.Из графика (рис. 2) видно, что скорость локомотива в течение первой и шестой секунд одинакова и равна 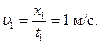(1)

В моменты времени t₁ = 3,5 с и t₂ = 4,5 с координата x не изменяется. Это значит, что в эти моменты скорость равна 0. (2)

Так как на участке (Г – Д) движение равноускоренное, и в момент t₂ = 4,5 с скорость равна нулю, то на этом участке скорость изменяется прямо пропорционально времени, и её график в момент t₂ =4,5 с проходит через 0 (рис. 3). (3)

На участке (Б – Г) движение также равноускоренное, и в момент t₁ = 3,5 с скорость равна нулю. На этом участке скорость тоже изменяется прямо пропорционально времени, и её график в момент t₁ = 3,5 с проходит через 0. (4)

На участке (А – Б) движение равноускоренное, а на графике (рис. 3) скорость представляет собой прямую, соединяющую скорости в точках А и Б. (5)

Из рис. 3 находим модуль ускорения модели электровоза: (6)

Критерии оценивания.

(6) Найдена скорость в начале и конце пути 1 балл + 1 балл

(7) Указаны моменты времени, когда скорость локомотива равна 0. 1 балл + 1 балл

(8) Построен график скорости на участке (Г – Д) 2 балла

(9) Построен график скорости на участке (Б – Г) 2 балла

(10) Построен график скорости на участке

(А – Б) 1 балла. Рис. 3

(11) Найден модуль ускорения 1 балл

Задача 3. Разбавленное топливо (Замятнин М.).

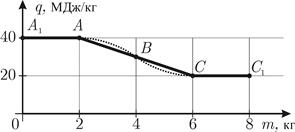
В бензобак автомобиля, в котором оставалось немного хорошего бензина, долили некачественное топливо. В результате удельная теплота сгорания q топлива, поступающего в двигатель, изменялась со временем (по мере расхода топлива) так, как показано на рис. 4. При данном выборе масштаба участки кривой АВ и ВС представляют собой дуги окружностей одного и того же радиуса. Считая КПД двигателя постоянным и равным 40%, определите, какую полезную работу совершил двигатель?

Возможное решение. Количество теплоты, выделившееся в двигателе при сгорании топлива, пропорционально площади под графиком. (1)

Поскольку дуга АВ выпуклая, а дуга ВС – вогнутая, то площадь под графиком зависимости q от m равна площади под графиком ломаной А₁АСС₁ (рис. 5). (2)

. (3)

С учетом КПД двигателя, его полезная работа

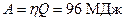(4)

Критерии оценивания.

(12) Указано, что энергия сгоревшего топлива пропорциональна площади под графиком

3 балла

(13) Указано, как вычислять площадь криволинейной трапеции 2 балла

(14) Получено числовое значение теплоты, выделившейся при сгорании топлива 2 балла

(15) Записано выражение для полезной работы двигателя 2 балла

(16) Получено числовое значение работы 1 балл