 |
Главная |
Алгоритм метода ветвей и границ для решения одномерных задач целочисленного программирования
|
из
5.00
|
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(Национальный Исследовательский Университет)
Факультет №3«Системы управления, 
информатика и электроэнергетика»
Кафедра №308«Информационные технологии» 
Курсовая работа
по курсу «Технический контроль и диагностика систем ЛА»
Вариант II (2)
Выполнила: Пахомова Вероника Юрьевна
Группа: 03-417
Проверил:доцент, к.т.н. Пискунов Вячеслав Алексеевич
Москва 2012 г.
Содержание
| Постановка задачи…………………………………………..……….…………………………………………….……..………3 |
| 1. Алгоритм метода ветвей и границ для решения одномерных задач целочисленного программирования ……………………………………………………………………………………………..………4 |
| 1.1. Теоретическая часть…………………………………………..……………………………………………...4 |
| 1.2. Практическая часть…………………………………………………………………………………………….8 |
| 1.3. Программные расчеты и сравнение результатов………………………………….……….15 |
| 2. Алгоритм метода динамического программирования…………………………….…….……….17 |
| 2.1. Теоретическая часть…………………………………………………………………………………………17 |
| 2.2. Практическая часть………………………………………………………………………………….……….22 |
| 2.3. Программные расчеты и сравнение результатов……………………………………….….24 |
| Выводы………………………………………………………………………………………….……………………………25 |
| Список используемой литературы…………….………………………………………………………………26 |
| Приложение 1……………………………………………………………………………………………………………………….27 |
| Приложение 2……………………………………………………………………………………………………………………….38 |
Постановка задачи
Определить набор параметров контроля из десяти непересекающихся параметров для получения максимального значения выражения  при ограничении
при ограничении  двумя методами:
двумя методами:
· метод ветвей и границ;
· метод динамического программирования.
Написать программы для реализации решения поставленной задачи.
Сравнить результаты при ручном расчёте и программном.
Сделать выводы.
Алгоритм метода ветвей и границ для решения одномерных задач целочисленного программирования
1.1 Теоретическая часть
В математическом анализе рассматривается класс задач, объединенных понятием задачи целочисленного программирования. В общем виде они могут быть сформулированы как максимизация некоторого выражения в условиях ограничений.
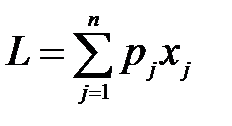 Рассмотрим следующую задачу целочисленного программирования. Требуется максимизировать выражение
Рассмотрим следующую задачу целочисленного программирования. Требуется максимизировать выражение
(1.1)
 при ограничениях
при ограничениях
(1.2)
xj  {0;1}, j=1,…,n, (1.3)
{0;1}, j=1,…,n, (1.3)
причем pj ≥0, cj≥0.
Решение задачи может быть получено с помощью метода ветвей и границ.
Метод ветвей и границ использует последовательно-параллельную схему построения дерева возможных вариантов. Первоначально ищут допустимый план и для каждого возможного варианта определяют верхнюю границу целевой функции. Ветви дерева возможных вариантов, для которых верхняя граница ниже приближенного решения, из дальнейшего рассмотрения исключают.
Эффективность вычислительных алгоритмов зависит от точности и простоты способа определения верхней границы возможных решений и точности определения приближенного решения. Чем точнее способ определения верхней границы целевой функции, тем больше бесперспективных ветвей отсекается в процессе оптимизации. Однако увеличение точности расчета верхних границ связано с возрастанием объема вычислений. Например, если для оценки верхней границы использовать симплекс-метод, то результат будет достаточно точным, но потребует большого объема вычислительной работы.
Рассмотрим алгоритм решения задачи (1.1) — (1.3) методом ветвей и границ с простым и эффективным способом оценки верхней границы целевой функции.
Множество U переменных xj рассматривается как три множества.
S -множество фиксированных переменных, вошедших в допустимое решение; Es — множество зависимых переменных, которые не могут быть включены в множество S, так как для них выполняется неравенство

GS — множество свободных переменных, из которых производится выбор для включения в S очередной переменной.
Обозначим h1j = pj/cj и допустим, что xj  S (j= 1, . .., k < п), вычисляется указанное отношение и параметры номеруются (ранжируются) в соответствии с ранжировкой:
S (j= 1, . .., k < п), вычисляется указанное отношение и параметры номеруются (ранжируются) в соответствии с ранжировкой:
 h1,k+1 ≥h1,k+2≥ ...≥h1l, l≤n, (1.4)
h1,k+1 ≥h1,k+2≥ ...≥h1l, l≤n, (1.4)
(1.5)
(1.6)
Условия (1.5), (1.6) означают, что в множество S без нарушения неравенства (1.2) можно дополнительно ввести элементы хк+1, хк +2,..., хl-1. При введении в множество S элементов хк+1, хк +2,..., хl неравенство (1.2) не выполняется.
Для определения верхней границы решения может быть использовано
выражение:
 (1.7)
(1.7)
где

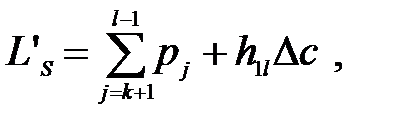 (1.8)
(1.8)
(1.9)
Из условий (1.1)-(1.3) следует, что L's не меньше максимального значения величины

 при ограничениях
при ограничениях
Поясним процесс определения L'S графиком (рис. 1.1). Строим кусочнолинейную функцию L(с) с убывающим значением градиента h. Вычисляем с'1 и по графику находим L'S.
Выбор очередной переменной для включения в множество S производится с помощью условия:
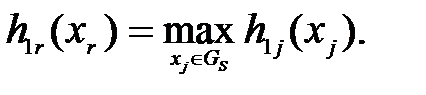 (1.10)
(1.10)
Для выбранной переменной хr определяются величины РS(xr) и РS( xr), т.е. в S включается хr = 1 или хr = 0.
Если в процессе решения окажется, что в множестве GS нет элементов, которые могут быть введены в множество S без нарушения ограничения (1.5), то полученное решение  принимается в качестве первого приближенного решения L0.
принимается в качестве первого приближенного решения L0.
Все вершины дерева возможных вариантов, для которых выполняются условия QS ≤ L0 из дальнейшего рассмотрения исключаются.
Из оставшихся ветвей выбирается ветвь с максимальным значением РS, и процесс поиска оптимального варианта продолжается. Если в процессе решения будет найдено  , то полученное решение принимается в качестве нового приближенного результата. Вычислительная процедура заканчивается, если для всех оставшихся ветвей выполняется условие РS ≤ L0.
, то полученное решение принимается в качестве нового приближенного результата. Вычислительная процедура заканчивается, если для всех оставшихся ветвей выполняется условие РS ≤ L0.
1.2 Практическая часть
Дано:
Нормированные вероятности отказов для элементов Qi, затраты на контроль i-ого параметра C(xi).
| № | ||||||||||
| Qi | 0,04 | 0,15 | 0,13 | 0,08 | 0,02 | 0,09 | 0,06 | 0,08 | 0,03 | 0,04 |
| C(xi) |
Найти: Выбрать такие параметры, чтобы C≤18 при Q=Qmax.
Решение:
Для удобства расчетов проранжируем таблицу 4 в порядке убывания 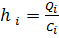 и присвоим новые номера элементам, следующим образом:
и присвоим новые номера элементам, следующим образом:
| №(i) | ||||||||||
| №(j) | ||||||||||
| Qj | 0,15 | 0,08 | 0,04 | 0,13 | 0,09 | 0,06 | 0,03 | 0,08 | 0,04 | 0,02 |
| C(xj) | ||||||||||
| hj | 0,15 | 0,04 | 0,04 | 0,0325 | 0,03 | 0,03 | 0,03 | 0,0267 | 0,008 | 0,0033 |
Значение l определяет сумма q1+ q2+ q3+ q4+ q5+ q6+ q7 + q8 =17, отсюда l=9

при l = 9,  ,
,  ,
,



Первый шаг
Выбор очередной переменной для включения в множество S производится с помощью условия: 






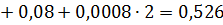

Второй шаг
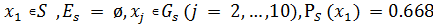
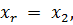


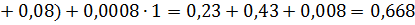



Третий шаг 
Выбираем очередную переменную: 


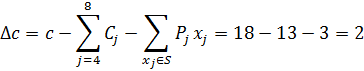
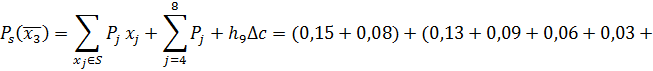


Четвертый шаг 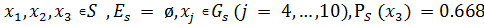
Выбираем очередную переменную: 





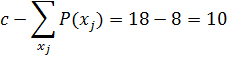
Пятый шаг 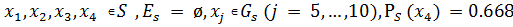
Выбираем очередную переменную: 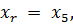

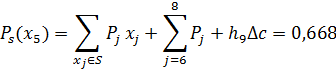


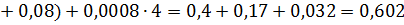

Шестой шаг 
Выбираем очередную переменную: 



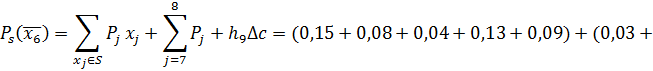


Седьмой шаг 
Выбираем очередную переменную: 





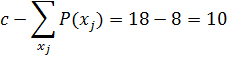
Восьмой шаг 
Выбираем очередную переменную: 

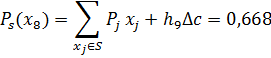


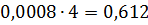

Девятый шаг

Во множестве GS нет элементов, которые могут быть введены в множество S без нарушения ограничения  , то полученное решение Ls принимается в качестве первого приближенного решения L0.
, то полученное решение Ls принимается в качестве первого приближенного решения L0.
Так как все вершины дерева, для которых выполняется условие Qs£ L0, из дальнейшего рассмотрения исключаются, а так же данный набор параметров обеспечивает максимальную вероятность, то процесс расчета прекращается. Результаты всех расчетов приведены в табл. 1.
Таблица 1
| № | S | Es | Gs | Рs | xr | Рs(xr) | Рs( 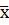 r) r)
| L0 |
| ø | ø | 1-10 | 0.668 | x1 | 0.668 | 0.526 | ||
| x1 | ø | 2-10 | 0.668 | x2 | 0.668 | 0.604 | ||
| x1, x2 | ø | 3-10 | 0.668 | x3 | 0.668 | 0.636 | ||
| x1, x2, x3 | ø | 4-10 | 0.668 | x4 | 0.668 | 0.57 | ||
| x1, x2, x3, x4 | ø | 5-10 | 0.668 | x5 | 0.668 | 0.602 | ||
| x1, x2, x3, x4, x5 | ø | 6-10 | 0.668 | x6 | 0.668 | 0.624 | ||
| x1, x2, x3, x4, x5, x6 | ø | 7-10 | 0.668 | x7 | 0.668 | 0.646 | ||
| x1, x2, x3, x4, x5, x6, x7 | 9,10 | 8, | 0.668 | x8 | 0.668 | 0.612 | ||
| x1, x2 , x3 , x4, x5,, x6 , x7, x8 | 9,10 | ø | - | - | - | - | 0.66 |
Таким образом, в состав контролируемых параметров входит набор X1; X2; X3: X4; X5; X6; X7; X8 или, если смотреть первоначальную нумерацию X2; X3; X4; X6; X7; X8; X9; X10.
1.3 Программные расчеты и сравнение результатов
Наряду с ручным расчётом, решение задачи реализовано с помощью программного алгоритма, написанного на языке программирования Delphi 7.0.
Листинг программы представлен в приложении 1.
Результаты программного расчёта сохраняются в текстовый файл kr1.txt и представлены на рисунке 1 для первых 4-ёх шагов, а итоговое решение на рисунке 2.
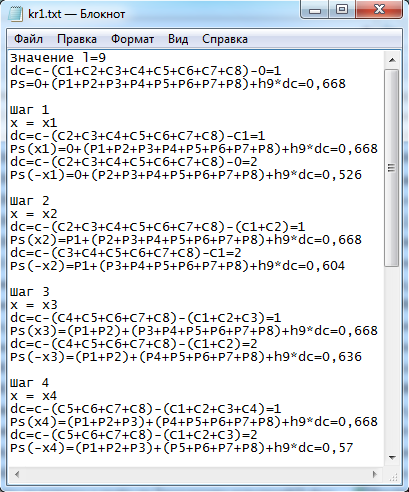
Рис. 1. Результат работы программы для 4-х шагов

Рис.2. Результат работы программы
Результаты программы и результаты ручного расчета совпали.
|
из
5.00
|
Обсуждение в статье: Алгоритм метода ветвей и границ для решения одномерных задач целочисленного программирования |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

