 |
Главная |
Разработка блок-схемы машинного алгоритма и программы
|
из
5.00
|
Программа для нахождения минимума будет начинаться с функции L(x0,y0,e), входными параметрами которой являются x0 - точка приближения по x, y0 - точка приближения по y и точность приближенного решения e. Равномерный поиск реализован основным соотношением:
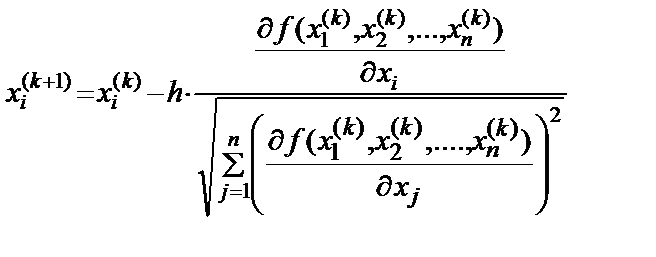
Результатом функции будет значение аргументов функции, доставляющих минимум рассматриваемой функции, само значение этого минимума. Приведем блок-схему машинного алгоритма (Рисунок 2).
| Конец |
| Начало |
Выбираем стартовую точку 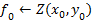
|
Вычисляем производные

|
| Задаем шаг h |
Получаем новую точку
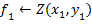
|
Делаем равномерный шаг в антиградиентном направлении
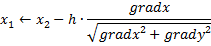

|
| h > e |
Вывод

|

|
Уменьшаем шаг
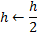
|
Присваиваем новые значения
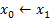

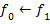
|
| Нет |
| Да |
| Нет |
| Да |
Рисунок 2 – Блок-схема программы
Реализация градиентного метода в Mathcad представлена на рисунке 3.

Рисунок 3 – Листинг программы в Mathcad
Результат выполнения программы представлен на рисунке 4.
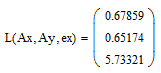
Рисунок 4 – Результат выполнения программы
Результат, выданный программой, показывает координаты точки минимума x=0.67859 y=0.65174 и значение функции в этой точке Z(x,y)=5.73321.
Построим графики функций (Рисунок 5, Рисунок 6).
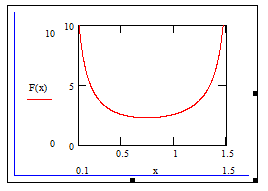
Рисунок 5 – График функции F(x)

Рисунок 6 – График функции H(y)
По графикам на рисунках 5 и 6 видно, что экстремум функции попадает в заданную область ограничений.
Так же построим 3D график нашей функции цели Z(x,y).
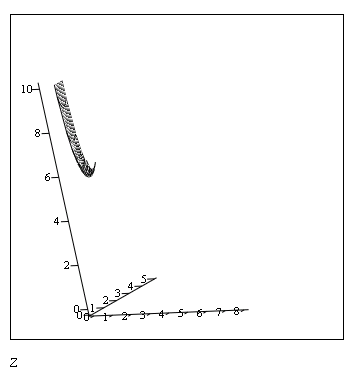
Рисунок 7 – 3D график функции цели Z(x,y)
Проверка необходимых и достаточных условий экстремума для найденной точки минимума
Для проверки необходимого условия существования экстремума функции найдем первую производную Zpr(x,y) от целевой функции Z(x,y) и подставим получившиеся координаты точек x и y. Производная равна нулю (учитывая допустимую погрешность), следовательно, необходимое условие существования экстремума выполнено.
А для проверки достаточного условия нужно построить матрицу Гессе и с помощью встроенной функции в Mathcad найти её определитель, подставив координаты полученной точки.
Реализуем алгоритм проверки необходимого условия в Mathcad. Листинг программы представлен на рисунке 8.

Рисунок 8 – Листинг программы по проверке необходимого условия
Реализуем программу для проверки достаточного условия. Листинг программы представлен на рисунке 9.
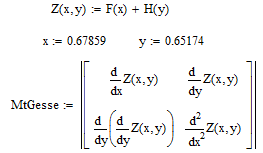
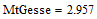
Рисунок 9 – Листинг программы по проверке достаточного условия
По выполненной программе на рисунке 9 можно сделать вывод, что матрица Гессе положительно определена, это означает то что мы нашли точку минимума.
|
из
5.00
|
Обсуждение в статье: Разработка блок-схемы машинного алгоритма и программы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

