 |
Главная |
Общие теоретические основы
|
из
5.00
|
Обход в ширину. Алгоритм Дейкстры.
КУРСОВАЯ РАБОТА
студентки 1 курса 131 группы
специальности 090301.65 Компьютерная безопасность
факультета компьютерных наук и информационных технологий
Шакировой Виолетты Александровны
Научный руководитель (руководитель)
аспирант _____________ Гавриков А. В.
Зав. кафедрой
профессор, к.ф -м.н. _____________ Салий В. Н.
Саратов 2013
СОДЕРЖАНИЕ
Введение 3
1 Теоретическая часть 4
1.1 Общие теоретические основы 4
1.2 Алгоритмы обхода графа 4
1.2.1 Обход в ширину 4
1.2.1.1 Метод обхода 4
1.2.1.2 Алгоритм обхода 5
1.2.1.3 Анализ обхода 6
1.2.1.4 Корректность 6
1.2.2 Поиск кратчайшего пути 7
1.2.2.1 Метод обхода 7
1.2.2.2 Алгоритм обхода 9
1.2.2.3 Анализ обхода 9
1.2.2.4 Корректность 10
2 Практическая часть 13
2.1 Реализация обхода в ширину 12
2.2 Реализация алгоритма Дейкстры 14
Заключение 16
Список использованных источников 17
ВВЕДЕНИЕ
Поиск кратчайшего пути – вопрос, который востребован сегодня повсеместно. Нахождение кратчайшего пути используется практически везде, начиная от поиска оптимального маршрута между двумя объектами на местности, в системах автопилота, нахождение оптимального маршрута при перевозках, коммутации информационного пакета в Internet и т.д. Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Существует множество алгоритмов поиска кратчайших маршрутов. Три наиболее эффективных из них:
1) алгоритм Дейкстры (используется для нахождения оптимального маршрута между двумя вершинами);
2)алгоритм Флойда (для нахождения оптимального маршрута между всеми парами вершин);
3)алгоритм Йена (для нахождения k-оптимальных маршрутов между двумя вершинами)
В данной курсовой работе будет подробно рассмотрен базисный алгоритм - обход в ширину, и сам поиск кратчайшего пути между двумя вершинами во взвешенном графе – алгоритм Дейкстры. В первой части работы я предоставлю теоретические знания, которые дадут некоторые начальные сведения о графах. В последующих главах будет представлен метод обхода, алгоритм на псевдоязыке и сама реализация в виде программного кода.
Теоретическая часть
Общие теоретические основы
Введем соответствующую терминологию.
Граф – это упорядоченная пара множеств 
 – это подмножество вершин (или узлов), а
– это подмножество вершин (или узлов), а 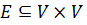 – упорядоченное или не упорядоченное множество ребер, соединяющих пары вершин из
– упорядоченное или не упорядоченное множество ребер, соединяющих пары вершин из  .
.
Взвешенный граф – граф  , где каждому ребру или вершине присваивается числовое значение, или вес.
, где каждому ребру или вершине присваивается числовое значение, или вес.
Не взвешенный граф – граф  , где разные вершины или ребра не различаются по весу.
, где разные вершины или ребра не различаются по весу.
Ациклический граф – граф, не имеющий циклов.[1]
Временная сложность алгоритма – это функция размера входных и выходных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера. Во многих задачах размер выхода не превосходит или пропорционален размеру вход – в этом случае можно рассматривать временную сложность как функцию размера только входных данных.[2]
Список смежности – эффективный способ представления разреженных графов. Это структура, где для каждой вершины хранится в динамическом списке смежные ей вершины.
Разреженный граф – граф, в котором в действительности ребра определены только для малой части возможных пар вершин.[1].
1.2 Алгоритмы обхода графа
1.2.1 Обход в ширину
1.2.1.1 Метод обхода
Обход в ширину (breadth-first traversal) является основой для многих важных алгоритмов для работы с графами.
Пусть задан невзвешенный граф  в котором выделена исходная вершина
в котором выделена исходная вершина  . Для алгоритма нам потребуются очередь, которая сначала содержит только
. Для алгоритма нам потребуются очередь, которая сначала содержит только  , и множество посещенных вершин
, и множество посещенных вершин  , которое изначально тоже содержит только
, которое изначально тоже содержит только  . На каждом шаге алгоритм вынимает из начала очереди вершину, рассматривает все исходящие из нее ребра и добавляет все связанные с ней не посещенные вершины в
. На каждом шаге алгоритм вынимает из начала очереди вершину, рассматривает все исходящие из нее ребра и добавляет все связанные с ней не посещенные вершины в  и в конец очереди. Если очередь пуста, то алгоритм завершает работу.
и в конец очереди. Если очередь пуста, то алгоритм завершает работу.
Поиск в ширину также может построить дерево поиска в ширину. Изначально оно состоит из одного корня  . Когда мы добавляем не посещенную вершину в очередь, то добавляем ее и ребро, по которому мы до нее дошли, в дерево. Поскольку каждая вершина может быть посещена не более одного раза, она имеет не более одного родителя. После окончания работы алгоритма для каждой достижимой из
. Когда мы добавляем не посещенную вершину в очередь, то добавляем ее и ребро, по которому мы до нее дошли, в дерево. Поскольку каждая вершина может быть посещена не более одного раза, она имеет не более одного родителя. После окончания работы алгоритма для каждой достижимой из  вершины
вершины  путь в дереве поиска в ширину соответствует кратчайшему пути от
путь в дереве поиска в ширину соответствует кратчайшему пути от  до
до  в
в  .
.
Также можно для каждой вершины 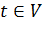 считать длину этого пути, равную
считать длину этого пути, равную  . Можно считать, что для не посещенных вершин эта длина бесконечно велика. Тогда на каждом шаге длина пути до
. Можно считать, что для не посещенных вершин эта длина бесконечно велика. Тогда на каждом шаге длина пути до  равна
равна  , если
, если  посещена и
посещена и  в противном случае. Отсюда следует, что если на каждом шаге обновлять длины путей, то информация о множестве
в противном случае. Отсюда следует, что если на каждом шаге обновлять длины путей, то информация о множестве  является избыточной, и его можно не хранить.[4]
является избыточной, и его можно не хранить.[4]
1.2.1.2 Алгоритм обхода
Ниже представлен псевдокод алгоритма поиска в ширину.
Таблица 1.2 – Псевдокод обхода в ширину.
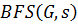






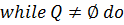



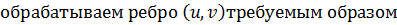




 [1]
[1]
1.2.1.3 Анализ обхода
Оценим время работы для входного графа  . В очередь добавляются только не посещенные вершины, поэтому каждая вершина посещается не более одного раза. Операции внесения в очередь и удаления из нее требуют
. В очередь добавляются только не посещенные вершины, поэтому каждая вершина посещается не более одного раза. Операции внесения в очередь и удаления из нее требуют  времени, так что общее время работы с очередью составляет
времени, так что общее время работы с очередью составляет  операций. Для каждой вершины
операций. Для каждой вершины  рассматривается не более
рассматривается не более  ребер, инцидентных ей. Так как
ребер, инцидентных ей. Так как  , то время, используемое на работу с ребрами, составляет
, то время, используемое на работу с ребрами, составляет  . Поэтому общее время работы алгоритма поиска в ширину —
. Поэтому общее время работы алгоритма поиска в ширину —  .
.
1.2.1.4. Корректность
Утверждение: В алгоритме поиска в ширину очередь всегда содержит сначала некоторое количество вершин с расстоянием  ,а потом некоторое количество вершин с расстоянием
,а потом некоторое количество вершин с расстоянием  (возможно, нулевое).
(возможно, нулевое).
▲ Докажем это утверждение индукцией по числу выполненных алгоритмом шагов.
База: изначально очередь содержит только одну вершину  с расстоянием 0, утверждение верно.
с расстоянием 0, утверждение верно.
Переход: пусть после l-го шага алгоритма очередь содержит p вершин с расстоянием  и
и  вершин с расстоянием
вершин с расстоянием  . Тогда на
. Тогда на  шаге мы извлечем из очереди одну вершину и добавим в нее все не посещенные
шаге мы извлечем из очереди одну вершину и добавим в нее все не посещенные  вершин связанные с ней; расстояние до них, очевидно, будет равно
вершин связанные с ней; расстояние до них, очевидно, будет равно  . У нас останется
. У нас останется 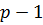 (возможно, 0) вершин с расстоянием
(возможно, 0) вершин с расстоянием  и
и 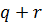 вершин с расстоянием
вершин с расстоянием  , что соответствует нашему инварианту. ■
, что соответствует нашему инварианту. ■
Теорема: Алгоритм поиска в ширину в невзвешенном графе находит длины кратчайших путей до всех достижимых вершин.
▲ Допустим, что это не так. Выберем из вершин, для которых кратчайшие пути от  найдены некорректно, ту, настоящее расстояние до которой минимально. Пусть это вершина
найдены некорректно, ту, настоящее расстояние до которой минимально. Пусть это вершина  , и она имеет своим предком в дереве обхода в ширину
, и она имеет своим предком в дереве обхода в ширину  , а предок в кратчайшем пути до
, а предок в кратчайшем пути до  – вершина
– вершина  .
.
Так как w – предок u в кратчайшем пути, то 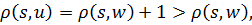 и расстояние до
и расстояние до  найдено верно,
найдено верно, 
Так как 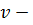 предок
предок  в дереве обхода в ширину, то
в дереве обхода в ширину, то 
Расстояние до  найдено некорректно, поэтому
найдено некорректно, поэтому  Подставляя сюда два последних равенства, получаем
Подставляя сюда два последних равенства, получаем  то есть,
то есть, 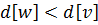 . Из ранее доказанной леммы следует, что в этом случае вершина
. Из ранее доказанной леммы следует, что в этом случае вершина  попала в очередь и была обработана раньше, чем
попала в очередь и была обработана раньше, чем  . Но она соединена с
. Но она соединена с  , значит,
, значит,  не может быть предком
не может быть предком  в дереве обхода в ширину. Мы пришли к противоречию, следовательно, найденные расстояния до всех вершин являются кратчайшими.[4]
в дереве обхода в ширину. Мы пришли к противоречию, следовательно, найденные расстояния до всех вершин являются кратчайшими.[4] 
1.2.2 Поиск кратчайшего пути
1.2.2.1 Метод обхода
Алгоритм Дейкстры является предпочтительным методом поиска кратчайших путей в графах со взвешенными ребрами и/или вершинами. Основная идея данного алгоритма очень похожа на основную идею алгоритма Прима. В каждом цикле мы добавляем одну вершину к дереву вершин, для которых мы знаем кратчайший путь из вершины  . Так же, как и в алгоритме Прима, мы сохраняем информацию о наилучшем пути на данное время для всех вершин вне дерева и вставляем их в дерево в порядке возрастания веса.
. Так же, как и в алгоритме Прима, мы сохраняем информацию о наилучшем пути на данное время для всех вершин вне дерева и вставляем их в дерево в порядке возрастания веса.
Разница между алгоритмом Дейкстры и алгоритмом Прима состоит в том, как они оценивают привлекательность каждой вершины вне дерева. В задаче поиска минимального остовного дерева нас интересовал только вес следующего возможного ребра дерева. А при поиске кратчайшего пути нам нужна также информация о ближайшей к вершине  вне дерева, т.е., кроме веса нового ребра, мы хотим знать еще и расстояние от вершины
вне дерева, т.е., кроме веса нового ребра, мы хотим знать еще и расстояние от вершины  к смежной с ней вершине дерева.
к смежной с ней вершине дерева.
Алгоритм находит кратчайший путь от заданной начальной вершины  ко всем другим вершинам графа, включая требуемую конечную вершину
ко всем другим вершинам графа, включая требуемую конечную вершину  .
.
Допустим, что кратчайший путь от вершины  к вершине t графа G проходит через определенную промежуточную вершину
к вершине t графа G проходит через определенную промежуточную вершину  . Очевидно, что этот путь должен содержать кратчайший путь от вершины
. Очевидно, что этот путь должен содержать кратчайший путь от вершины  к вершине x, в качестве префикса, ибо в противном случае можно было бы сократить путь
к вершине x, в качестве префикса, ибо в противном случае можно было бы сократить путь 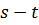 , используя более короткий префиксный путь
, используя более короткий префиксный путь  . Таким образом, прежде чем найти кратчайший путь от начальной вершины
. Таким образом, прежде чем найти кратчайший путь от начальной вершины  к промежуточной вершине
к промежуточной вершине  .
.
Алгоритм Дейкстры работает поэтапно, находя на каждом этапе кратчайший путь от вершины  к некой новой вершине. Говоря конкретно, вершина
к некой новой вершине. Говоря конкретно, вершина  такова, что сумма
такова, что сумма  минимальна для всех необработанных 1≤ i≤ n, где
минимальна для всех необработанных 1≤ i≤ n, где 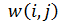 – длина ребер между вершинами i и j, a
– длина ребер между вершинами i и j, a  – длина кратчайшего пути между ними.
– длина кратчайшего пути между ними.
Здесь напрашивает стратегия, аналогичная динамическому программированию. Кратчайший путь от вершины  к самой себе является тривиальным, при условии отсутствия ребер с отрицательным весом, поэтому
к самой себе является тривиальным, при условии отсутствия ребер с отрицательным весом, поэтому  . Если
. Если  является самым легким ребром, входящим в вершину
является самым легким ребром, входящим в вершину  , то это означает, что
, то это означает, что  . Определив кратчайший путь к вершине
. Определив кратчайший путь к вершине  , мы проверяем все исходящие из нее ребра, чтобы узнать, не существует ли лучшего пути из начальной вершины
, мы проверяем все исходящие из нее ребра, чтобы узнать, не существует ли лучшего пути из начальной вершины  к какой-либо неизвестной вершине через вершину
к какой-либо неизвестной вершине через вершину  .
.
1.2.2.2 Алгоритм обхода
Ниже представлен псевдокод алгоритма поиска кратчайшего пути.
Таблица 1.2 – Псевдокод алгоритма Дейкстры.
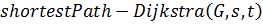
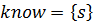




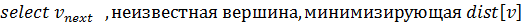



1.2.2.3 Анализ обхода
Временная сложность алгоритма Дейкстры, в том виде, как он реализован здесь, равна  .
.
Длина кратчайшего пути от начальной вершины start к созданной вершине t равна точно значению distance[t]. Каким образом мы можем найти сам путь с помощью алгоритма Дейкстры? Мы следуем обратным указателям на родительские узлы от вершины t, пока мы не дойдем до начальной вершины (или пока не получим -1, если такого пути не существует).
Алгоритм работает правильно только на графах, в которых нет ребер с отрицательным весом. Дело в том, что при построении пути может встретиться ребро с отрицательным весом настолько большим по модулю, что оно полностью изменит оптимальный путь от вершины s к какой-то другой вершине, которая уже включена в дерево.[1]
1.2.2.4. Корректность
Теорема: Пусть  ориентированный взвешенный граф, вес рёбер которого неотрицателен, s – стартовая вершина. Тогда после выполнения алгоритма Дейкстры
ориентированный взвешенный граф, вес рёбер которого неотрицателен, s – стартовая вершина. Тогда после выполнения алгоритма Дейкстры  для всех
для всех  где
где 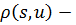 длина кратчайшего пути из вершины
длина кратчайшего пути из вершины  в вершину
в вершину  .
.
▲ Докажем по индукции, что в момент посещения любой вершины 
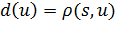 .
.
На первом шаге выбирается  , для нее выполнено:
, для нее выполнено: 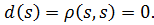
Пусть для  первых шагов алгоритм сработал верно, и на
первых шагов алгоритм сработал верно, и на  шагу выбрана вершина
шагу выбрана вершина  . Докажем, что в этот момент
. Докажем, что в этот момент  . Для начала отметим, что для любой вершины
. Для начала отметим, что для любой вершины  , всегда выполняется
, всегда выполняется  . (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть
. (алгоритм не может найти путь короче, чем кратчайший из всех существующих). Пусть  — кратчайший путь из
— кратчайший путь из  в
в  ,
,  — первая не посещённая вершина на
— первая не посещённая вершина на  ,
,  — предшествующая ей (следовательно, посещённая). Поскольку путь
— предшествующая ей (следовательно, посещённая). Поскольку путь  кратчайший, его часть, ведущая из
кратчайший, его часть, ведущая из  через
через  в
в  , тоже кратчайшая, следовательно
, тоже кратчайшая, следовательно  . По предположению индукции, в момент посещения вершины
. По предположению индукции, в момент посещения вершины  выполнялось
выполнялось  , следовательно, вершина
, следовательно, вершина 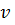 тогда получила метку не больше чем
тогда получила метку не больше чем 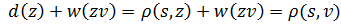 , следовательно,
, следовательно,  С другой стороны, поскольку сейчас мы выбрали вершину
С другой стороны, поскольку сейчас мы выбрали вершину  , её метка минимальна среди не посещённых, то есть
, её метка минимальна среди не посещённых, то есть  , где второе неравенство верно из-за ранее упомянутого определения вершины
, где второе неравенство верно из-за ранее упомянутого определения вершины  в качестве первой, не посещённой вершины на
в качестве первой, не посещённой вершины на  , то есть вес пути до промежуточной вершины не превосходит веса пути до конечной вершины вследствие неотрицательности весовой функции. Комбинируя это с
, то есть вес пути до промежуточной вершины не превосходит веса пути до конечной вершины вследствие неотрицательности весовой функции. Комбинируя это с  , имеем
, имеем  , что и требовалось доказать.
, что и требовалось доказать.
Поскольку алгоритм заканчивает работу, когда все вершины посещены, в этот момент  для всех
для всех  . [3]■
. [3]■
Практическая часть
В практической части работы будут представлены коды реализующие алгоритм обхода в ширину и алгоритм нахождения кратчайшего пути.
|
из
5.00
|
Обсуждение в статье: Общие теоретические основы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

