ЧИСЛЕННОЕ РЕШЕНИЕ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ В ПАКЕТЕ МАТЕМАТИЧЕСКИХ РАСЧЕТОВ MATHCAD

Введением конечно-разностных соотношений в уравнение теплопроводности – дифференциальное уравнение второго порядка в частных производных – отыскание решения уравнения свелось к определению решений систем линейных алгебраических уравнений относительно значений температуры в точках сетки. Эти системы могут решаться любым из методов решения систем линейных алгебраических уравнений. В пакете MathCAD существует функция решения систем линейных алгебраических уравнений методом Гаусса lsolve. Воспользуемся ею для получения решения уравнения теплопроводности (1.1) с начальным (1.11) и граничными (1.12) условиями. Аргументами функции lsolve являются матрица коэффициентов перед неизвестными и столбец свободных членов системы. В данном случае предстоит многократное решение системы с одинаковой матрицей коэффициентов. Изменяются столбцы свободных членов.

Начиная решение, введем исходные данные и вычислим значения температуры на нулевом временном слое по начальным условиям (1.11). Далее зададим матрицу коэффициентов системы - матрицу А и столбец свободных членов (1.18) (рис.3.1). Находим решение системы, т.е. температуру на первом временном слое u1, и показываем результат вычислений (рис.3.2). Определена температура для внутренних узлов сетки. Для того чтобы найти температуру на втором временном слое, нужно решить систему с измененным столбцом свободных членов. Для получения решения на втором временном слое нужно пересчитать свободный столбец системы и снова ее решить. Особенностью вычисления в пакете MathCAD является то, что индексы у векторов отсчитываются от нуля, поэтому появляется несоответствие в записи формул. Решение для второго слоя u2 приведено на рис. 3.3.

Рис. 3.1. Подготовка данных для решения уравнения теплопроводности на первом временном слое

Рис. 3.2. Решение уравнения теплопроводности на первом временном слое

Рис. 3.3. Решение уравнения теплопроводности на втором временном слое

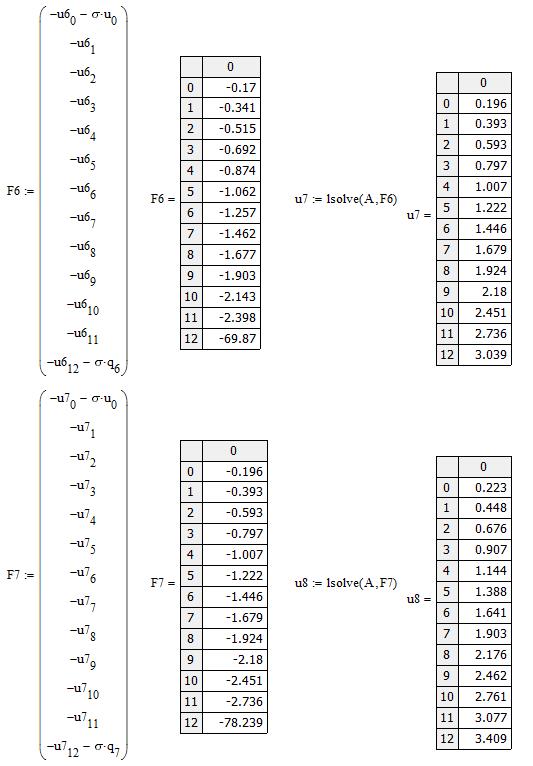
Рис. 3.4. Полное решение в MathCAD

Повторяя вычисления столбца свободных членов и решения системы еще десять раз, получим вектора u1, u2, u3,…, u15, содержащие значения температуры во внутренних точках сетки. Полное решение представлено на рис. 3.4. Графическое полного решения можно увидеть на рис. 3.7.

Далее предстоит собрать в одну матрицу начальные значения, краевые и вычисленные во внутренних узлах.

Рис. 3.5. Формирование матрицы с результатами

Рис. 3.6. Результат решения уравнения теплопроводности

Рис. 3.7. Графическое преставление решения