Точное эталонное аналитическое решение системы (3) дифференциальных уравнений

Расчёт динамики разгона и торможения судна

Вариант №«Чайка»

 

 

Выполнил:

Студент ФМиАТ

 

 

Проверила:

Галина Н В

 

 

Нижний Новгород

2013г.

 

Содержание:

 

Введение.

 

1. Постановка задачи и ее математическая модель.

 

1.1. Общая задача, описания динамики разгона (торможения)

судна.

 

1.2. Математическая модель неустановившегося движения.

2. Методы и алгоритмы решения задачи.

 

2.1. Формирование функций R(V) и T(V).

 

2.2. Точное эталонное аналитическое решение системы (3)

дифференциальных уравнений.

 

3. Исходные данные.

 

4. Этапы выполнения работы.

 

5. Модельная задача №1.

 

6. Модельная задача №2.

 

7. Модельная задача №3.

 

8. Реализация в MathCAD

 

9. Общий вывод

 

Постановка задачи и ее математическая модель.

Общая задача, описания динамики разгона (торможения) судна.

Из курса теоретической механики известно, что в соответствии принципам Даламбера неустановившееся движение тела описывается вторым законом Ньютона. Поскольку в данной задаче рассчитывается движение лишь в направлении одной из осей координат (в данном случае оси “X”), то достаточно записать уравнения движения в проекции на ось “X” и решать его относительно скорости “V” в направлении оси “X” и пройденного по этой координате пути “S”.

 

Математическая модель неустановившегося движения судна.

Основным уравнением задачи в этом случае является уравнение второго закона Ньютона в проекции на ось координат “X”.

 

m*a = F (1)

 

Здесь:

m – масса тела;

а = dV/dt – ускорение тела;

F – сумма всех сил, действующих на судно, в проекции на ось “X”.

Равнодействующая сила F складывается из двух сил:

R – сопротивление движению судна;

Т – тяга движения (как правило, гребного винта).

 

Из физических соображений понятно, что сопротивление R зависит от скорости движения (чем больше скорость “V”, тем больше сопротивление R) и направлена против скорости “V”, т.е. в отрицательном направлении оси “X”. Тяга, создаваемая гребным винтом, также зависит от скорости судна, но действует в противоположном направлении силе сопротивления R, т.е. направлена в положительном направлении оси “X”.

 

С учетом сказанного, уравнение (1) можно записать в виде:

 

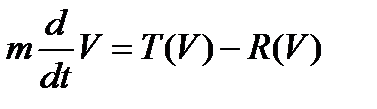(2)

 

Таким образом, получено обыкновенное дифференциальное уравнение 1-го порядка относительно скорости движения судна “V”.

Для определения пройденного за время “разгона” пути “S” к этому уравнению (2) необходимо добавить уравнение dS/dt=V, являющееся определением понятия – “скорость”. Таким образом, математической моделью задачи считается система из двух дифференциальных уравнений 1-го порядка, записанных в каноническом виде:

 

(3)

 

Здесь функции R(V) и T(V) являются заданными и находятся по испытаниям моделей судна и гребного винта. Как правило, эти функции задаются либо графически, либо таблично.

Для решения системы уравнений (3) необходимо задать начальные условия. Обычно они задаются в виде t=0 или V=Vn.

 

 

Методы и алгоритмы решения задачи.

Формирование функций R(V) и T(V).

В курсовой работе исходными данными являются функции R(V) и T(V), которые представлены в графическом виде. Решением данной задачи является снятие контрольных точек с графиков (R(V) - 16-20 точек и T(V) – 8-10 точек) включая первую и последнюю и заполнение таблиц исходных данных (необходимо помнить, что расчеты производятся в системе СИ).

 

Аппроксимация исходных данных

 

По сформированным таблицам этих функций необходимо:

1) выбрать класс аппроксимирующей функции (если выбран полином, то необходимо выбрать его степень исходя из вида кривой по характерным точкам, выбранным из контрольных);

2) определить коэффициенты аппроксимации;

3) рассчитать и вывести на дисплей графики аппроксимирующих функций.

 

Точное эталонное аналитическое решение системы (3) дифференциальных уравнений.

Для отладки программы решения общей (припроизвольныхR(V) и T(V)) системы (3) целесообразно задать эти функции в виде полиномов 1-й степени.

 

(4)

 

здесь коэффициенты аппроксимации.

 

Обозначим (5)

 

Тогда уравнение (2) примет вид:

 

(6)

 

Это простейшее дифференциальное уравнение с разделяющимися переменными. Разделим переменные и проинтегрируем:

 

(7)

 

Здесь начальные условия входят в пределы интегрирования. Вычисляя интегралы, получаем:

 

(8)

 

Потенцируя, получаем:

 

 

 

(9)

 

 

Это и есть точное решение уравнения (6). При t=0 имеем V=VH, т.е. начальное условие выполнено автоматически. При разгоне коэффициент и при 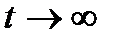получаем:

 

(10)

 

 

(11)

 

При торможении судна конечная скорость V равна нулю. Учитывая это, подставляем формулу (8) в формулу (11) и получаем значение пройденного пути при торможении:

 

При отладке программы в общем случае получаемое численное решение с линейными аппроксимациями T(V) и R(V) сравнивается с точным, для проверки правильности алгоритма и программы и выбора тела интегрирования.

 

Исходные данные.

Судно «Чайка»

Масса судна: 10000 кг

Таблица№1 значений функций R(V) и T(V):

	Исходные данные:
	Т - сила тяги движителя	R - сила сопротивления воде
	V, км/ч	V, м/c	T(V)	T(V), H	V, км/ч	V, м/c	R(V)	R(V),H
		2,777778				2,777778
		4,166667				4,166667
		5,555556				5,555556
		6,944444				6,944444
		8,333333				8,333333
		9,722222				9,722222
		11,11111				11,11111
		13,88889				13,88889
		16,66667				16,66667
		19,44444				19,44444
		22,22222				22,22222
		23,61111				23,61111
		27,77778				27,77778
		28,33333				28,33333