Метод сопряжённых направлений Пауэлла

 

4.1 Описание алгоритма

 

Метод ориентирован на решение задач с квадратичными целевыми функциями. Основная идея алгоритма заключается в том, что если квадратичная функция:

приводится к виду сумма полных квадратов

то процедура нахождения оптимального решения сводится к 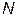одномерным поискам по преобразованным координатным направлениям.

В методе Пауэлла поиск реализуется в виде:

вдоль направлений , , называемых 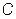-сопряженными при линейной независимости этих направлений.

Сопряженные направления определяются алгоритмически. Для нахождения экстремума квадратичной функции 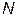переменных необходимо выполнить одномерных поисков.

 

4.2 Алгоритм метода

 

Шаг 1. Задать исходные точки , и направление . В частности, направление может совпадать с направлением координатной оси;

Шаг 2. Произвести одномерный поиск из точки в направлении получить точку , являющуюся точкой экстремума на заданном направлении;

Шаг 3. Произвести одномерный поиск из точки в направлении получить точку ;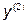

Шаг 4. Вычислить направление ;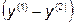

Шаг 5. Провести одномерный поиск из точки (либо 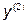) в направлении 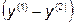c выводом в точку .

 

4.3 Нахождение минимума целевой функции методом сопряжённых направлений Пауэлла.

 

Исходные данные:

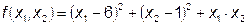
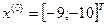- начальная точка

 

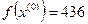
1. , .

 

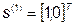2.

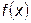а) Найдем значение , при котором минимизируется в направлении :

Откуда ; .

Значение функции в этой точке: ;

Продифференцируем полученное выражение по , получим:

. Приравняв его к нулю, находим ;

Получили

б) Аналогично находим значение минимизирующее функцию в направлении :

Откуда ; .

Значение функции в этой точке: ;

Продифференцируем полученное выражение по , получим:

. Приравняв его к нулю, находим ;

Получили

в) Найдем значение минимизирующее :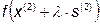

Откуда ; .

Значение функции в этой точке: ;

Продифференцируем полученное выражение по , получим:

. Приравняв его к нулю, находим ;

Получили

 

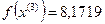
3.

 

4. Найдем такое значение , при котором минимизируется в направлении .

Откуда ; .

Значение функции в этой точке: ;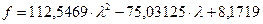

Продифференцируем полученное выражение по , получим:

. Приравняв его к нулю, находим ;

Получили

Таким образом, получили точку , значение функции в которой равно , что совпадает со стационарной точкой

Рисунок 4. Графическое пояснение метода сопряженных направлений Пауэлла

Метод Коши

 

5.1 Описание алгоритма

 

В методе Коши или методе наискорейшего спуска в качестве направления поиска выбирается направление антиградиента.

- градиент функции

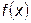
Алгоритм метода выглядит следующим образом:

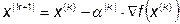, где - градиент.

Значение на каждой итерации вычисляется путем решения задачи одномерного поиска экстремума 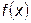вдоль направления градиента . Если в качестве взять некоторое положительное число, то получится простейший градиентный алгоритм:

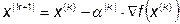
Одно из главных достоинств метода Коши является его устойчивость, так как всегда выполняется условие:

Однако вблизи экстремума скорость сходимости алгоритма становится недопустимо низкой, так как вблизи экстремума значение градиента стремится к нулю.

 

5.2 Нахождение минимума целевой функции методом Коши.

Исходные данные:

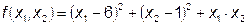
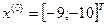- начальная точка (начальное приближение)

 

Вычислим компоненты градиента:

Начальное приближение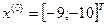

1. Новое приближение определим по формуле:

Выбираем такое, чтобы минимизировать функцию

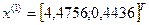
2. Далее найдем точку:

3. Далее найдем точку:

4. Далее найдем точку:

После 4 итераций найдено достаточно точное значение минимума, при котором значение целевой функции в точке , .

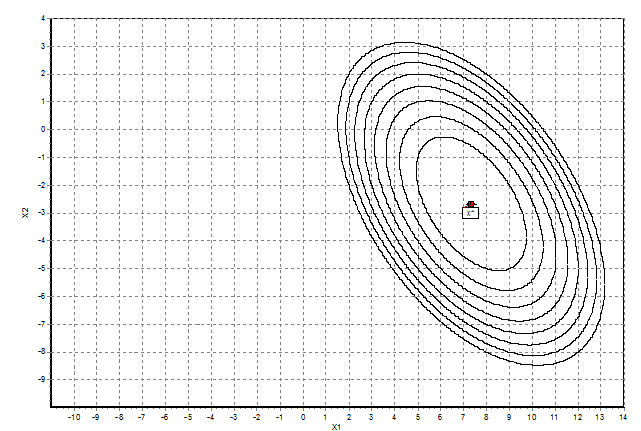Рисунок 5. Графическое пояснение метода Коши

Метод Ньютона

 

6.1Описание алгоритма

 

Этот метод использует информацию о вторых производных целевой функции. Эта информация появляется при квадратичной аппроксимации целевой функции, когда при её разложении в ряд Тейлора учитываются члены ряда до второго порядка включительно. Алгоритм метода выглядит следующим образом:

, где:

- гессиан (матрица Гессе)

В случае, когда гессиан положительно определён, направление по методу Ньютона оказывается направлением спуска.

 

6.2 Нахождение минимума целевой функции методом Ньютона.

 

Исходные данные:

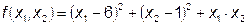
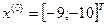- начальная точка;

;

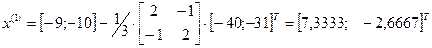
Таким образом, точка минимума , значение функции в которой найдена за одну итерацию.

Рисунок 6. Графическое пояснение метода Ньютона