Элементы теории контрактов

В настоящее время экономическая теория предлагает более реалистическое описание самого процесса принятия решений, чем это предпринималось раньше. Стандартная неоклассическая модель изображает человека как существо гиперрациональное. Один из новых подходов (Неоинституциональный) отличается большей трезвостью. Это находит выражение в двух его важнейших поведенческих предпосылках --ограниченной рациональности и оппортунистического поведения.

Первая отражает факт ограниченности человеческого интеллекта. Знания, которыми располагает человек, всегда неполны, его счетные и прогностические способности далеко не беспредельны, совершение логических операций требует от него времени и усилий. Одним словом, информация ресурс дорогостоящий. из-за этого агенты вынуждены останавливаться не на оптимальных решениях, а на тех, что кажутся им приемлемыми исходя из имеющейся у них ограниченной информации. Их рациональность будет выражаться в стремлении экономить не только на материальных затратах, но и на своих интеллектуальных усилиях. При прочих равных условиях они будут предпочитать решения, предъявляющие меньше требований к их предсказательным и счетным возможностям.

Оппортунистическое поведение определяется О.Уильямсоном, который ввел это понятие в научный оборот, как "преследование собственного интереса, доходящее до вероломства" (self-interest-seeking-with-guile). Речь идет о любых формах нарушения взятых на себя обязательств, например -- уклонении от условий контракта. Индивиды, максимизирующие полезность, будут вести себя оппортунистически (скажем, предоставлять услуги меньшего объема и худшего качества), когда это сулит им прибыль.

Одной из основных формы оппортунистического поведения является отлынивание. "Отлынивание" (shirking): оно возникает при асимметрии информации, когда агент точно знает, сколько им затрачено усилий, а принципал имеет об этом лишь приблизительное представление (так называемая ситуация "скрытого действия"). В таком случае возникает и стимул, и возможность работать не с полной отдачей. Особенно остро встает эта проблема, когда люди работают сообща ("командой") и личный вклад каждого определить очень трудно.

Приложение 2

Строгое решение нелинейной задачи определяемой соотношениями (24), (25),(26), (27) может быть получено с использованием теоремы Куна-Таккера. Для этого введем новые переменные 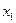и , где и .

Целевая функция (24) примет вид (П.1),

(П.1)

Ограничение (17) преобразуется к виду

(П.2)

Ограничение (20) преобразуется к виду

(П.3)

Ограничение (23) преобразуется к виду

(П.4)

Очевидно, что решение оптимальное решение задачи (П.1)-(П.4) достигается в той же точке, что и решение задачи определяемой соотношениями (24), (25),(26), (27).

Область допустимых значений функции нелинейной оптимизации (П.1)-(П.4) в координатах 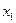и определяемая соотношениями (П.2), (П.3) и (П.4) приведена на рис.П.1 и заштрихована тройной штриховкой. Заметим, что соотношение (П.3) можно удалить, при этом область допустимых значений функции не изменится.

Рис.П1. Область допустимых значений задачи нелинейной оптимизации в координатах 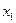и и линии уровня целевой функции.

Введем функции , и используя соотношения, приведенные ниже.

	(П.5)
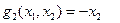
	(П.6)
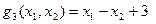
	(П.7)

Преобразуем соотношения (П.2) и (П.4) используя вновь введенные функции. Ограничения (П.4) преобразуется к виду

	(П.8)
	(П.9)

Ограничение (П.2) преобразуется к виду

(П.10)

Область допустимых значений функции нелинейной оптимизации в координатах 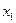и определяемая соотношениями (П.8), (П.9) и (П.10) приведена на рис.П.2 и заштрихована двойной штриховкой. На рисунке также показаны линии уровня оптимизируемой функции и направление градиента в некоторых точках.

Рис.П2. Область допустимых значений задачи нелинейной оптимизации в координатах 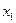и и линии уровня целевой функции.

Все функции ограничений-неравенств афинны, 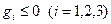а значит, выпуклы, поэтому область допустимых значений в задаче выпукла. Заметим, что если взять некоторую точку внутри области, например, , то эта точка будет допустимой и все неравенства в ней выполняются строго . Отсюда следует что область регулярна во всех точках.

Для проверки выпуклости вычислим её Гессиан (матрицу вторых производных).

(П.11)

.

Главные миноры равны и положительны, поэтому по критерию Сильвестра матрица положительна определена. Поскольку для выпуклости дважды дифференцируемой функции необходимо и достаточно неотрицательной определенности Гессиана, то функция выпукла во всей области определения. Таким образом, условия Куна-Таккера будут необходимыми и достаточными условиями, определяющими решение задачи.

Вычислим градиенты функций задачи.

	(П.12)
	(П.13)
	(П.14)
	(П.15)

Чтобы использовать условия Куна-Таккера, необходимо установить набор активных ограничений-неравенств в точке решения.

Взаимное расположение области допустимых значении, линии уровня и направления градиента на рис.П2 позволяют высказать следующие соображения относительно возможной точки условного минимума. Каждая линия уровня является эллипсом, определяемым уравнением . Возьмем, например, точку А с координатами эта точка не принадлежит области. Через нее проходит линия уровня . Будем мысленно раздвигать эллипс (линию) уровня в направлении градиента (в направлениях показанных стрелками), это будет соответствовать расширению эллипса. Будем расширять эллипс до тех пор, пока она не коснется заштрихованной области. Можно предположить, что касание произойдет в угловой точке В с координатами (рис.П.3), Поэтому, предположим, что активными являются ограничения 1 и 3, которые определяют подозрительную точку В на рис.П.3. Тогда для этой точки система будет иметь вид

(П.16)

Используя явное выражение для этих функций, получаем следующее соотношение.

(П.17)

Подставив 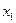и , получим следующее соотношение для определения и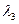

(П.18)

Откуда следует следующая система уравнений

(П.19)

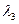Отсюда следует, что и . Поскольку и положительны и все условия теоремы К-Т выполнены, то. точка В действительно является решением оптимизационной задачи. Геометрический смысл соотношения (П.18) показан на рис.П.3. вектор антиградиент можно разложить по векторам и с положительными коэффициентами и 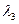, т.е. проекции на векторы и направлены также как и сами вектора. Таким образом, оптимальное решение задачи (П.1)-(П.4) достигается при и . Поэтому оптимальное решение исходной задачи определяемой соотношениями (24), (25),(26), (27) достигается при и . Целевая функция (П.1) при этом равна .

Рис.П3. Область допустимых значений задачи нелинейной оптимизации в координатах 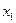и и линии уровня целевой функции.

Приложение 3