Определение оценок коэффициентов уравнения регрессии методом МНК

Пассивный эксперимент.

Является традиционным методом, при котором ставится большая серия опытов с поочередным варьированием каждой переменной. К пассивному эксперименту относится сбор исходного статистического материала в режиме нормальной эксплуатации на промышленном объекте. Обработка данных для получения математической модели осуществляется методом классического регрессионного и корреляционного анализа.

Активный эксперимент.

Ставится по заранее составленному плану. При этом предусматривается одновременное изменение всех параметров, влияющих на процесс, что позволяет сразу установить силу взаимосвязей параметров и как следствие сократить число опытов. В результате статистической обработки получают математическую модель, связывающую параметр оптимизации через выходной параметр с переменными параметрами, варьируемыми в процессе опыта.

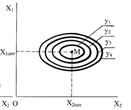
Факторы, факторное пространство, поверхность отклика.

Факторами принято называть независимые переменные .

Координатное пространство с координатами называют факторным пространством.

Геометрическое изображение функций отклика в факторном пространстве называют поверхностью отклика.

Например, зависимость выхода реакции (y) в процентах от температуры (х1) и концетрации (х2).

Разложение модели в ряд Тейлора.

При использовании статистических методов математическая модель представляется в виде полинома отрезка ряда Тейлора, в котором разлагается неизвестная зависимость

в выражение вида:

; ;

;

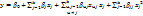
В связи с тем, что в реальном процессе всегда существует неуправляемые и неконтролируемые переменные, изменение величины носит случайный характер. Поэтому при обработке эксперимента получают выборочные коэффициенты регрессии , являющиеся оценками теоретических коэффициентов. Тогда уравнение регрессии, получаемое при обработке данных имеет вид:

- свободный член уравнения регрессии;

- линейный эффект;

– квадратичный эффект;

- эффекты взаимодействия.

Определение оценок коэффициентов уравнения регрессии методом МНК.

- свободный член уравнения регрессии;

- линейный эффект;

– квадратичный эффект;

- эффекты взаимодействия.

Коэффициенты определяют по методу наименьших квадратов:

– оценочные значения полученные по модели

– экспериментальные данные

N – объем выборки из всей совокупности значений.

Разность между N и числом взаимосвязей, положенных на эту выборку l, называют числом степеней свободы:

При нахождении уравнения регрессии число взаимосвязей равно числу определяемых коэффициентов.