Примеры линейных операторов

3.1

Системой линейных уравнений с неизвестными называются соотношения вида

(3.1)

где - коэффициенты системы, - свободные члены, - неизвестные системы.

Система (3.1) называется однородной, если все свободные члены . Система (3.1) называется неоднородной, если хотя бы один из свободных членов .

Решением системы называется совокупность чисел , при подстановке которых в уравнения системы вместо соответствующих неизвестных каждое уравнение системы превращается в тождество. Система, не имеющая ни одного решения, называется несовместной, или противоречивой. Система, имеющая хотя бы одно решение, называется совместной.

Совместная система называется определенной, если она имеет единственное решение. Если совместная система имеет более одного решения, то она называется неопределенной. Однородная система всегда совместна, так как имеет, по крайней мере, нулевое решение . Выражение для неизвестных , из которого можно получить любое конкретное решение системы, называют ее общим решением, а любое конкретное решение системы – ее частным решением. Две системы с одними и теми же неизвестными эквивалентны (равносильны), если каждое решение одной из них является решением другой или обе системы несовместны.

Рассмотрим методы решения систем линейных уравнений.

3.2

Одним из основных методов решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Суть этого метода состоит в сведении системы линейных уравнений к ступенчатому виду. При этом над уравнениями приходится проводить следующие элементарные преобразования:

1. Перестановка уравнений системы.

2. Прибавление к одному уравнению другого уравнения.

3. Умножение обеих частей уравнения на число, отличное от нуля.

4. Прибавление к одному уравнению другого, умноженного на некоторое число, отличное от нуля.

5. Вычеркивание уравнений вида , т.е. тождеств .

В результате элементарных преобразований система преобразуется в эквивалентную ей систему.

Рассмотрим алгоритм метода Гаусса. Пусть дана система вида (3.1). Предположим, что в этой системе коэффициент . Заметим, что этого всегда можно достигнуть перестановкой уравнений системы. Для исключения неизвестной во всех уравнениях, начиная со второго, умножим первое уравнение системы последовательно на числа и добавим соответственно ко 2-му, 3-му, ..., - му уравнению системы.

В результате система примет вид:

Продолжая этот процесс дальше, исключим неизвестную из всех уравнений, начиная с третьего. Для этого умножим второе уравнение на числа и добавим к 3-му, ..., к - му уравнению системы. Следующие шаги метода Гаусса осуществляются аналогично. Если в результате преобразований получится тождественное уравнение, то вычеркнем его из системы. Если на некотором шаге метода Гаусса получается уравнение вида:

(3.2)

тогда рассматриваемая система несовместна и дальнейшее ее решение прекращается. Если же уравнение вида (3.2) не встретится при выполнении элементарных преобразований, то не более чем через - шагов система (3.1) будет преобразована к ступенчатому виду:

(3.3)

где . Если , то говорят, что система свелась к треугольному виду. В этом случае система имеет единственное решение, которое находим, решая систему снизу вверх.

Если , то говорят, что система свелась к трапециидальному виду. В этом случае система является неопределенной. Для нахождения общего решения системы в этом случае выбирают 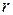главных и 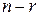свободных неизвестных. Например, неизвестные принимают за главные, а неизвестные принимают за свободные. Переносим свободные неизвестные в правую часть уравнений и выражаем главные неизвестные через свободные. В результате получаем общее решение системы:

(3.4)

Для получения частного решения системы необходимо будет в (3.4) придать свободным переменным конкретные значения.

Заметим, что так как в методе Гаусса все преобразования выполняются над коэффициентами при неизвестных уравнений и свободными членами, то на практике обычно этот метод применяют к матрице, составленной из коэффициентов при неизвестных и столбца свободных членов. Эту матрицу называют расширенной. С помощью элементарных преобразований эту матрицу сводят к ступенчатому виду. После чего по полученной матрице восстанавливают систему и применяют к ней все предыдущие рассуждения.

Пример 1. Решить систему:

.

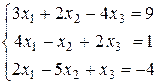Решение. Составляем расширенную матрицу и сводим ее к ступенчатому виду:

~^*) ~^**) ~ ^***)

~ ~^****) .

^*) – первую строку умножили на и добавили ко второй, полученную строку записали на первое место (цель этого преобразования получить единицу в первом столбце); оставили без изменения вторую строку на втором месте (можно было сюда записать первоначальную первую строку) и третью строку на своём месте.

^**) – умножили первую строку на и на и добавили ко второй и третьей соответственно.

^***) – вторую строку умножили на .

^****) – вторую строку умножили на и добавили к третьей.

Матрица свелась к треугольному виду, следовательно, система имеет единственное решение.

Восстанавливаем систему и решаем её снизу вверх.

Пример 2. Решить систему:

.

Решение. Составляем расширенную матрицу и сводим её к ступенчатому виду:

~ ~ .

Заметим, что выполнялись преобразования те же, что и в примере 1.

Данная система не совместна, так как последняя строка матрицы соответствует уравнению , которое решения не имеет.

Пример 3. Решить систему:

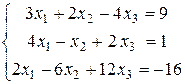
Решение. Составляем расширенную матрицу и сводим ее к ступенчатому виду:

~ ~ ~^*)

~ .

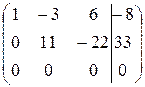^*) - вторую строку умножили на и вычеркнули третью строку.

Матрица свелась к трапецеидальному виду, следовательно, система является неопределенной:

Пусть - свободная неизвестная. Тогда получаем общее решение системы:

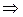
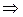
Замечание 1. При решении однородной системы линейных уравнений методом Гаусса на практике выписывают основную, а не расширенную матрицу системы. И сводят ее к ступенчатому виду.

Замечание 2. Метод Гаусса применим для любой системы линейных уравнений, в том числе и для системы, у которой число уравнений не равно числу неизвестных.

3.3

Выяснить вопрос о совместности системы и о числе ее решений помогает следующая теорема.

Теорема (Критерий совместности системы линейных уравнений). Система линейных уравнений (3.1) совместна тогда и только тогда, когда ранг основной матрицы системы (матрицы 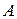) равен рангу расширенной матрицы (матрицы ). В противном случае, т.е. если , то система не совместна. Если , где - число неизвестных системы, то система определенная. Если , то система неопределенная.

Применим эту теорему для рассмотренных в п.3.2 примеров.

Для примера 1. и число неизвестных , т.е. система определенная.

Для примера 2. , поэтому система несовместна.

Для примера 3. , число неизвестных , поэтому система является неопределенной.

3.4

Пусть дана система линейных уравнений с неизвестными:

(3.5)

Рассмотрим еще один метод решения систем линейных уравнений – метод Крамера, основанный на следующей теореме.

Теорема (правило Крамера). Если в системе линейных уравнений с неизвестными (система вида (3.5)) определитель, составленный из коэффициентов при неизвестных отличен от нуля, то система имеет единственное решение, которое находится по формулам

, (3.6)

где – определитель, полученный из определителя заменой 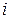-го столбца столбцом свободных членов.

Доказательство. Пусть в системе (3.5) определитель . Обозначим – алгебраические дополнения 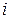-го столбца определителя . Умножим 1-е уравнение системы на , 2-е – на , …, -е – на и сложим полученные уравнения. В результате получим

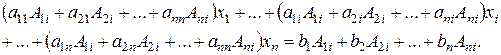(3.7)

Учитывая, что сумма произведений элементов строки (столбца) на их алгебраические дополнения есть определитель системы, а сумма произведений элементов строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю, получаем, что левая часть (3.7) равна .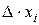

Несложно заметить, что правая часть (3.7) есть определитель , раскрытый по элементам 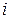-го столбца , т.е.

.

Таким образом, (3.7) можно записать в виде:

. (3.8)

Откуда при и получаем формулы (3.6), т.е. формулы Крамера.

Замечание. Методом Крамера можно решать только системы, в которых число уравнений равно числу неизвестных и основной определитель системы отличен от нуля.

Пример 4. Решить систему из примера 1 методом Крамера

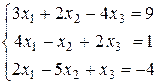
Решение. Вычисляем основной определитель системы:

Вычисляем определители :

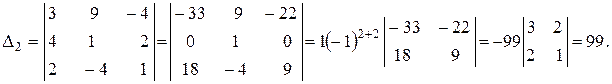
Получаем

3.5

Квадратная матрица 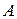называется обратимой, если существует такая матрица 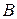, что выполняется условие:

. (3.9)

В этом случае матрица 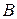называется обратной к 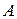и обозначается , т.е. 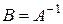. Тогда матрицы 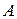и , называются взаимно-обратными.

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля, в противном случае матрица называется вырожденной.

Справедлива следующая теорема, доказательство которой дает способ вычисления обратной матрицы.

Теорема. Для любой невырожденной квадратной матрицы существует обратная матрица.

Доказательство. Пусть дана матрица . Заменим каждый элемент матрицы 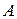его алгебраическим дополнением и транспонируем полученную матрицу, обозначив ее :

.

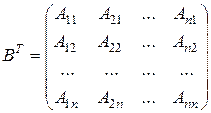Найдем произведение и . Обозначим произведение , где . Тогда по правилу нахождения произведения матриц

. (3.10)

Далее воспользуемся следующими свойствами.

1. Определитель матрицы равен сумме парных произведений элементов какой-либо строки (столбца) на их алгебраические дополнения.

2. Сумма произведений элементов какой-либо строки (столбца) определителя на алгебраические дополнения другой строки (столбца) определителя равна нулю.

Тогда, если в (3.10) , то , а если , то 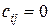. Таким образом,

,

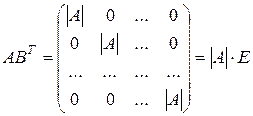где - единичная матрица.

Аналогично .

Тогда получаем формулу для нахождения обратной матрицы:

. (3.11)

Отсюда следует алгоритм нахождения обратной матрицы:

1. Находим определитель матрицы ; убеждаемся, что матрица невырожденная.

2. Вычисляем алгебраические дополнения элементов матрицы и составляем из них матрицу .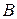

3. Транспонируем матрицу 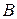, получаем матрицу .

4. Умножаем матрицу на число , т.е. каждый элемент матрицы делим на величину определителя матрицы .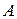

5. Полученная в п.4 матрица и есть обратная для данной матрицы, ее обозначаем .

Пример 5. Найти матрицу, обратную матрице

.

Решение.

1. (был вычислен ранее).

2.

 

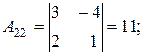
Таким образом, .

3. .

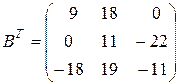4. .

5. Можно сделать проверку, получив и .

 

Другой способ нахождения обратной матрицы основан на элементарных преобразованиях. К матрице 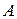приписывают единичную матрицу того же порядка. Далее с помощью элементарных преобразований получают слева единичную матрицу. Тогда матрица, которая окажется справа, и будет обратной для данной матрицы.

Пример 6.Для матрицы из примера 5 найти обратную матрицу с помощью элементарных преобразований.

Решение.

.

Таким образом,

,

т.е. ответ совпал с матрицей полученной в предыдущем примере.

3.6

Пусть дана система линейных уравнений с неизвестными (система (3.5)):

Обозначим - матрицу из коэффициентов при неизвестных, - матрицу-столбец из неизвестных, - матрицу-столбец свободных членов, т.е.

Несложно заметить, что тогда система (3.5) может быть записана в виде матричного уравнения

(3.12)

Умножим слева обе части уравнения (3.12) на матрицу, обратную матрице , т.е. на :

(3.13)

Учитывая, что из (3.13) получаем формулу для решения системы в матричной форме :

(3.14)

Пример 7. Решить систему из примеров 1 и 4 в матричной форме:

.

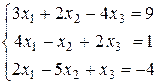Решение. Запишем систему в матричной форме:

Обозначим - матрицу из коэффициентов при неизвестных, - матрица из неизвестных, - матрица-столбец свободных членов. Обратная матрица для 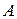была найдена в примерах 5 и 6: . Тогда находим решение системы:

.

Таким образом, .

Замечание. Матричный метод решения систем линейных уравнений применим только тогда, когда число уравнений системы равно числу неизвестных и матрица 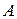является невырожденной (ограничения те же, что и в методе Крамера).

3.7

Как было отмечено выше, однородная система линейных уравнений всегда совместна, так как, согласно критерию совместности, ранги основной и расширенной матриц совпадают. Это следует из того, что для однородной системы расширенная матрица содержит столбец нулей – столбец свободных членов.

Для того чтобы однородная система имела единственное решение, необходимо и достаточно, чтобы ранг основной матрицы системы был равен числу неизвестных, т.е. .

Единственным решением однородной системы будет нулевое решение. Поэтому для существования ненулевых решений должно выполняться условие .

Если в однородной системе число уравнений равно числу неизвестных, то условие существования ненулевых решений состоит в равенстве нулю основного определителя системы, т.е. .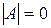

Лекция 4. Линейный оператор и его матрица. Собственные векторы и собственные значения линейного оператора.

План лекции

4.1. Линейные пространства. Понятие n-мерного вектора.

4.2. Размерность и базис линейного пространства. Координаты вектора линейного пространства.

4.3. Определение линейного оператора, примеры.

4.4. Матрица линейного оператора.

4.5. Собственные векторы и собственные значения линейного оператора, их нахождение.

4.1

Пусть L = {а,в,с,…} – множество элементов произвольной природы и P={a,b,g,…} – числовое поле. Определим операцию над элементами из L, условно называемую сложением, и операцию элементов из L на элементы из P, условно называемую умножением элементов из L на числа из P. Причём "a,bÎL:a+bÎL и "aÎL"aÎP:aaÎL.

Множество L называется линейным пространством над полем P (обозначается L(P)), если операции сложения элементов из L и умножения элементов из L на числа из P удовлетворяют аксиомам:

1^o. "a,bÎL:a+b=b+a – сложение коммутативно.

2^o. "а,b,cÎL:(a+b)+c = a+(b+c) – сложение ассоциативно.

3^o. $qÎL:"aÎL:a+q=q+a=a – существует нейтральный элемент по сложению.

4^o. "аÎL$(-a)ÎL:a+(-a)=(-a)+a=q – для любого элемента из L существует противоположный элемент по сложению.

5^o. "aÎL^1ÎP:a×1=1×a=a – в поле P существует 1 – нейтральный элемент по умножению.

6^o. "a,bÎP^"aÎL:(ab)a=a(ba) – ассоциативность относительного умножения элемента из L на произведение чисел из P.

7^o. "a,bÎP^"aÎL:(a+b)×a=aa+ba – дистрибутивность умножения элемента из L относительно суммы чисел из P.

8^o. "a,bÎL^"aÎP:a(a+b)=aa+ab – дистрибутивность умножения числа из P относительно суммы элементов из L.

Будем называть элементы из L векторами, поэтому линейное пространство L(P) называют и векторным пространством. Заметим, что рассмотренные ранее пространства V₂ и V₃ являются линейными. Однако, исходя из введенного определения линейного пространства, понятие вектора можно распространить далее и на не геометрические объекты.

Арифметическим вектором, или n-мерным вектором a будем называть упорядоченную последовательность из n чисел a₁,a₂,…,a_n и обозначать a=[a₁,a₂,…,a_n], где a_i( ) – компоненты вектора. Обозначим множество всех n-мерных векторов T_n и введем над ними операции сложения и умножения вектора на число из P по правилам:

1) "a=[a₁,a₂,…,a_n]ÎT_n^"b=[b₁,b₂,…,b_n]ÎT_n:

a+b=c=[a₁+b₁,a₂+b₂,…,a_n+b_n,]ÎT_n.

2) "a=[a₁,a₂,…,a_n]Î T_n^"lÎP:la=[la₁,la₂,…,la_n]Î T_n.

Можно проверить, что множество T_n удовлетворяет аксиомам 1^o - 8^o линейного пространства, и поэтому его называют арифметическим n-мерным пространством.

Можно проверить, что множество T_n всех n-мерных векторов a=[a₁,a₂,…,a_n] удовлетворяет аксиомам 1^o - 8^o линейного пространства, и поэтому его называют арифметическим n-мерным пространством.

4.2

Введенные ранее понятия линейно зависимой и линейно независимой систем векторов можно распространить на любую систему векторов, а не только на систему геометрических векторов.

Система векторов a₁,a₂,…,a_n линейного пространства L(P) называется линейно зависимой, если их линейная комбинация l₁a₁+l₂a₂+…+l_na_n равна нулю при условии, что не все l_i равны нулю ( ), и называется линейно независимой, если все l_i=0 ( ). Можно дать и другое определение. Система векторов a₁,a₂,…a_n – линейно зависимая, если один из векторов может быть выражен через другие, и линейно независимая – в противном случае.

Если в линейном пространстве L(P) имеется n линейно независимых векторов, но любые n+1 вектора этого пространства линейно зависимы, то пространство L(P) называют n-мерным, или говорят, что линейное пространство имеет размерность n. Записывают dim L(P)=n.

Таким образом, размерностью линейного пространства называют максимальное число линейно независимых векторов, которые можно выбрать в этом пространстве. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называют бесконечномерным, и пишут dim L(P)=¥.

Максимальное число линейно независимых векторов линейного пространства, через которые можно выразить любой другой вектор этого пространства, называется базисом этого пространства. Таким образом, число векторов базиса показывает, чему равна размерность этого пространства. Каждый вектор линейного пространства может быть единственным образом представлен в виде линейной комбинации векторов базиса. Так, если е₁,е₂,…,е_n – базис линейного пространства, то для любого вектора aÎL(P) разложение a=l₁е₁+l₂е₂+…+l_nе_n единственно. Коэффициенты разложения вектора по векторам базиса линейного пространства называются координатами вектора в данном базисе, т.е. можно записать a=(l₁,l₂,…,l_n)_B, где B={е₁, е₂,,…,е_n}.

Базис линейного пространства может быть выбран неоднозначно, но для данного линейного пространства количество векторов в базисе должно быть постоянно. Таким образом, постоянной существенной характеристикой линейного пространства является его размерность.

4.3

Будем говорить, что в линейном пространстве задано преобразование или оператор 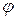, если каждому вектору 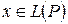по некоторому правилу поставлен в соответствие вектор .

Оператор 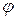называется линейным, если для любых двух векторов и из и для любого числа выполняются условия:

1. Образ суммы двух векторов равен сумме образов этих векторов, т. е.

. (4.1)

2. Образ произведения вектора на число равен произведению этого числа на образ вектора, т.е.

. (4.2)

Условия (4.1) и (4.2) в определении линейного оператора можно заменить одним условием: образ линейной комбинации векторов линейного пространства равен линейной комбинации образов этих векторов, т.е. для любых двух векторов и из и для любых чисел и :

. (4.3)

Примеры линейных операторов.

1. Линейное преобразование называется тождественным, если оно преобразует любой вектор в самого себя, и обозначается Е. Таким образом,

: E(x)=x.

2. Нуль-оператор – это оператор, переводящий любой вектор в нуль-вектор, и обозначается . Таким образом,

.

3. Оператор подобия задаётся правилом:

и .

4.4

Пусть в n-мерном линейном пространстве с базисом задан линейный оператор 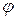. Образами базисных векторов будут векторы: 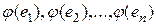этого же линейного пространства, поэтому каждый из них можно разложить единственным образом по векторам базиса:

(4.4)

Матрицей линейного оператора 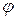в базисе В называется квадратная матрица , составленная из коэффициентов разложения образов базисных векторов по векторам базиса, т.е.

. (4.5)

Для приведённых в п. 4.3 примеров матрицы линейных операторов имеют вид:

, , .

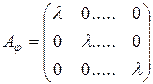Отметим тот факт, что матрица линейного оператора зависит от выбора базиса.

Пример 1. Проверить, что заданный в пространстве Т₃ оператор является линейным. Найти матрицу этого оператора в базисе , , .

Решение. Проверим условие (4.3):

и , : ,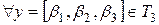

тогда

.

Следовательно, данный оператор является линейным.

Найдём образы базисных векторов , , :

.

Разлагаем образы базисных векторов по векторам базиса:

Для определения элементов матрицы линейного оператора получаем системы:

С учетом, что матрица из коэффициентов при неизвестных во всех полученных системах одинаковая, эти системы лучше решать матричным способом.

Запишем системы в матричной форме:

, ,

Находим обратную матрицу:

(проверить самостоятельно).

Следовательно, , , .

Таким образом, данный оператор в указанном базисе имеет матрицу:

.

4.5

Ненулевой вектор х линейного пространства называется собс