Полный факторный эксперимент первого порядка

 

u	X0	X1	X2	X3	X12	X13	X23	X123	Yср	Su
		-1	-1	-1				-1	526,768	536,0025
			-1	-1	-1	-1			598,235	589,0005
		-1		-1	-1		-1		443,256	445,665
				-1		-1	-1	-1	563,706	561,297
		-1	-1			-1	-1		587,796	578,5615
			-1		-1		-1	-1	622,325	631,5595
		-1			-1	-1		-1	544,434	542,025
									655,248	657,657

Построить матрицу-таблицу плана эксперимента.

 

Матрица-таблица плана эксперимента

 

 

Пояснить организацию проведения эксперимента. Указать реальные значения факторов в точках спектра плана эксперимента.

 

Для значения (-1) реальные значения факторов в точках спектра плана эксперимента равно:

 

.

.

 

Для значения (+1) реальные значения факторов в точках спектра плана эксперимента равно:

 

.

.

 

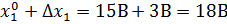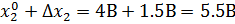Вычислить оценки дисперсии отклика в точках спектра плана и проверить их однородность.

Оценка дисперсии отклика.

N-количество опытов.

m-количество повторов одного опыта.

 

N=8; m=2.

 

С помощью критерия Кохрена проверяется однородность дисперсии. Величина критерия Кохрена вычисляется:

 

 

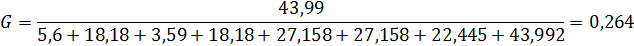
f₁-номер столбца.

f₂-номер строки.

f₁=m-1; f₂=N

G_kp для 5% равен 0,6798(табличное значение).

 

G_kp>G, дисперсия однородна и гипотеза принимается.

 

–дисперсия однородности.

 

 

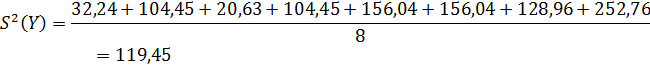
Определяем коэффициенты регрессии

 

 

 

 

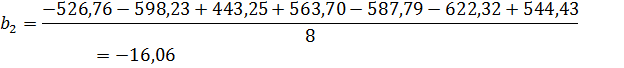
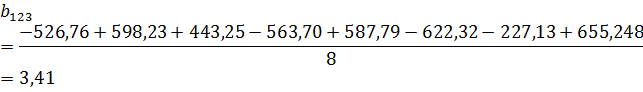
Коэффициент дисперсии

 

, -среднеквадротическое значение.

 

Оценить значимость коэффициентов уравнения регрессии

Коэффициент значимости:

 

Величина t-критическое сравнивается с t-критическим определенное по таблице (уровень значимости 5%)

 

f=N(m-1)-номер строки. f=8. t_kp =2.31(табличное значение).

 

Если ,то значения отбрасываются.

-отбрасываем

-отбрасываем

Найти математическую модель объекта исследования в виде линейного полинома с учетом возможных взаимодействий между факторами.

 

b₀X₀+b₁X₁+b₂X₂+b₃X₃+b₁₂X₁₂+b₂₃X₂₃

 

Подставляем численные значения в математическую модель ,с учетом знаков (x).

 

 

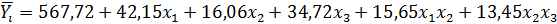
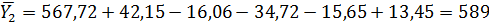
Проверка адекватности полученной модели:

Коэффициент адекватности :

 

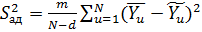.d=6 –количество значимых коэффициентов.

 

 

Для проверки гипотезы об адекватности необходимо использовать критерий Фишера:

 

, если ,то

f₁ и f₂ –номер столбца и строки соответственно.

 

для уровня значимости 5%

 

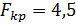(табличное значение).

 

 

. Если 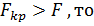математическая модель адекватна

 

Задание №3.

Ортогональный центральный композиционный плана второго порядка.

 

Построить матрицу-таблицу плана эксперимента.

u	X0	X1	X2	X12	X12-a	X22-a	Yср
		-1	-1		0,3333	0,3333	648,02
			-1	-1	0,3333	0,3333	510,7
г3		-1		-1	0,3333	0,3333	731,53
					0,3333	0,3333	632,76
		-1			0,3333	-0,6667	670,5
					0,3333	-0,6667	552,46
			-1		-0,6667	0,3333	595,02
					-0,6667	0,3333	697,4
					-0,6667	-0,6667	626,74

 

Указать кодированные значения факторов звездных точек.

α – Плече звездной точки

а - с помощью этого параметра приводим матрицу к ортогональному виду.

N₀ – Количество точек ядра плана.

N – Общее число точек плана.

m - количество повторов одного опыта.

m=2

N=9

N₀=4

 

Вычислить оценки дисперсии отклика в точках спектра плана и проверить их однородность.

 

 

 

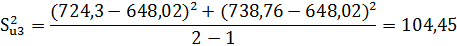
С помощью критерия Кохрена проверяется однородность дисперсии. Величина критерия Кохрена вычисляется:

 

f₁ и f₂ –номер столбца и строки соответственно.

 

f₁=m-1; f₂=N

 

G_kp для 5% равен 0,6385(табличное значение).

 

G_kp>G, дисперсия однородна и гипотеза принимается.

 

–дисперсия однородности.

 

 

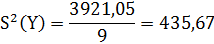
Оценить значимость коэффициентов уравнения регрессии.

 

 

 

 

 

 

 

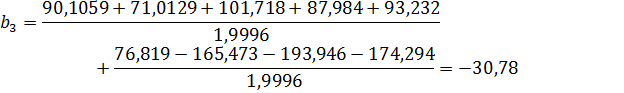
Вычислить оценки дисперсии отклика в точках спектра плана и проверить их однородность.

 

 

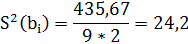
, -среднеквадротическое значение.

 

Коэффициент значимости:

 

 

Величина t-критическое сравнивается с t-критическим определенное по таблице (уровень значимости 5%):

 

f=N(m-1)-номер строки. f=9. t_kp =2,2622(табличное значение).

 

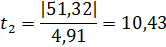
Если ,то значения отбрасываются.

 

-отбрасываем

 

Найти математическую модель объекта исследования в виде линейного полинома с учетом возможных взаимодействий между факторами.

 

b₀X₀+b₁X₁+b₂X₂+b₃X₃ +b₄X₄

Подставляем численные значения коэффициентов регрессии и знак (х)

 

*

 

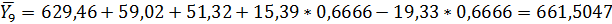
Проверить адекватность полученной модели.

 

Коэффициент адекватности :

 

.

 

d=5-количество значимых коэффициентов

 

 

Для проверки гипотезы об адекватности необходимо использовать критерий Фишера:

 

,если ,то

f₁ и f₂ –номер столбца и строки соответственно.

 

для уровня значимости 5%

 

 

 

. Если значит гипотеза об адекватности принимается, в противном случае гипотеза отвергается и переходит к более сложным уровням связи.

 

Заключение.

 

На первом этапе была собрана информация, необходимая для дальнейшего исследования, было выдвинуто предположение о виде закона распределения случайной величины и проведено доказательство данного предположения, были определены оценки параметров данного распределения.

Затем на втором этапе выяснялась зависимость между факторами, действующими на исследуемую величину, и изменение этой величины. Для предвидения влияния определенных факторов используется полный факторный эксперимент для построения регрессионной математической модели. Эта модель позволяет нормировать измерения вне зависимости от влияющих факторов или указывает на влияющее воздействие, которое необходимо устранить.
Несмотря на простоту методов, они представляют собой мощный механизм повышения качества продукции и могут использоваться для решения весьма обширного круга задач, когда приходится принимать решения в условиях действия многочисленных влияющих на процесс факторов.

 

 

Список литературы

 

1. Планирование и организация измерительного эксперимента / Е.Т. Володарский, Б.Н.Малиновский, Ю.М. Туз – К.: В.шк. Головное изд-во, 1987.

2. Романов В.Н. Планирование эксперимента: Учебное пособие. -Л.: СЗПИ, 1992.

3. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий. –М.: Наука, 1971.

4. Асатурян В.И. Теория планирования эксперимента. -М.: Радио и связь, 1983.

5. Математическое моделирование автоматизированных систем контроля и управления:Метод. указания / Авт.-сост. А.Ю. Сенкевич. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004.

6. Монахов О.И. "Идентификация объекта управления на основе планирования

эксперимента": Методические указания. - М.: МИИТ, 1998.