 |
Главная |
Формирование собственных m-файлов пользователя
|
из
5.00
|
В Matlab существует два типа m-файлов: программные (script-файлы) и функции (functions).
Создание m-файла удобнее всего выполнить с помощью встроенного блокнота-отладчика Matlab Editor/Debugger, хотя принципиально функция может быть создана с помощью любого текстового редактора.
Программные файлы (программы) содержат последовательность операторов и команд языка Matlab, представляющей собой запись определенного алгоритма вычислений. Все переменные, содержащиеся в script-файле, находятся в оперативной памяти компьютера, и остаются там даже после завершения работы программы (так называемые глобальные данные).
Выполнение программ происходит после указания в командной строке имени соответствующего файла без расширения или после использования меню File – Run Script…
Функции должны содержать в первой строке файла заголовок, имеющий формат:
function вых_параметр = имя_функции (список_вх_параметров)
После заголовка обычно записывают комментарий (непрерывную последовательность символов, начиная со второй строки m-функции и заканчивая первой командой или первой пустой строкой), обычно выполняющий роль помощи, который будет выводиться на экран при выполнении в командной строке инструкции
help имя_функции
Первая строка комментария-помощи, известная как m1-строка, включается в файл содержания данного каталога contents.m.
После комментария записывают последовательность операторов, составляющих тело функции и описывающих алгоритм преобразования входных параметров в выходные.
Сохранение функции следует выполнить в любой доступный каталог обязательно с именем, совпадающим с именем функции, и расширением .m.
Для выполнения функции к ней необходимо обратиться из другой функции, из программного файла или из командной строки, указав ее имя и в скобках – список фактических параметров (аргументов), каждый из которых к моменту вызова функции должен быть определен (иметь значение).
Входные и выходной параметры в описании функции являются формальными (не имеющими значений). Формальные параметры, а также вспомогательные переменные, используемые в операторах функции, являются локальными, то есть, их значения теряются после завершения работы функции. Функция не может изменить значения аргументов, даже если соответствующие им формальные входные параметры в процессе работы функции изменяются.
Если функция не требует наличия входных и (или) выходных параметров, они в заголовке функции указываются в виде пустого вектора [ ], или вообще опускаются.
Пример создания функции.
Создать функцию maxi(x), которая для заданного вектора определяет максимальный элемент и его адрес.
function [xm,im]=maxi(x)
% Пояснения к работе функции
% …
[m,n]=size(x);
if (m~=1)&(n~=1) % Если x - матрица
error('Ошибка в размерности аргумента');
end
k=length(x);
if k==1, xm=x; im=1; break; end
xm=x(1);
for i=2:k
if x(i)>xm xm=x(i); end
end
if nargout==2 % Два выходных параметра
im=find(x==xm);
end
Набранный текст функции необходимо сохранить в доступном каталоге в файле с именем maxi.m.
Пример работы с созданной функцией в командном окне Matlab выглядит следующим образом:
» y=[2 5 8 -1];
» maxi(y)
ans =
» [ymax imax]=maxi(y)
ymax =
imax =
» x=[1 2 8; 5 3 12];
» maxi(x)
??? Error using ==> maxi
Ошибка в размерности аргумента
» c=25;
» maxi(c)
ans =
Рациональное использование оперативной памяти в Matlab
для ускорения выполнения операций
Встроенные в Matlab операции над векторами и матрицами в целом выполняются намного быстрее, чем соответствующие им поэлементные операции. Поэтому следует стремиться к максимальной векторизации алгоритмов в m-файлах, особенно при больших объемах вычислений.
Например, в большом числе случаев возможно и целесообразно заменить циклические операции векторными или матричными:
clear all;
i = 1;
for t = 0:.1:10
i = i+1;
y(i) = sin(t);
end
% Время выполнения 2,31 сек
clear all;
t = 0:.1:10;
i = 1:length(t);
y = sin(t);
% Время выполнения 0,06 сек
Отсюда видно, что скорость выполнения операций, дающих практически тот же результат, возрастает в тридцать – сорок раз.
Продолжительность выполнения операций в Matlab может быть определена с помощью оператора, синтаксис которого имеет вид:
tic, операторы, toc
Если же какую-либо часть программы не удается векторизировать, выполнение циклических операций можно ускорить предварительным резервированием памяти под матрицы, в которые потом будут помещены результаты. Это особенно заметно при работе с большими массивами.
Глобальные переменные
Обычно каждая m-функция имеет локальные переменные, не доступные в других функциях, программных файлах и в рабочем пространстве (извне). Однако, если некоторые переменные необходимо сделать доступными извне, то в самой функции и в каждой из сред, использующих эти данные, следует такие переменные описать как глобальные:
global имя_переменных
Например,
global ALFA
global A MATRIX RADIUS
Принято идентификаторы таких глобальных переменных формировать заглавными буквами.
Пример. Изучить влияние коэффициентов a и b на решение системы дифференциальных уравнений
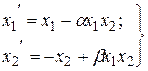
при  и при начальных условиях
и при начальных условиях 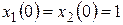 .
.
Создадим m-файл правых частей ДУ:
function xp = diffurav (t, x)
% Файл правых частей ДУ
global ALFA BETA
xp = [x(1) – ALFA*x(1)*x(2); –x(2) + BETA*x(1)*x(2)];
и сохраним его с именем diffurav.m в доступном каталоге пользователя.
В командной строке интерактивно вводим следующие операторы:
» global ALFA BETA
» ALFA=0.1; BETA=0.02;
» [t, x] = ode23('diffurav',[0 10],[1 1]);
» plot(t, x), grid on
Теперь в командной строке можно интерактивно менять значения a и b и получить новое решение системы ДУ без редактирования каких-либо файлов.
|
из
5.00
|
Обсуждение в статье: Формирование собственных m-файлов пользователя |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

