Последовательный критерий отношения правдоподобия

(критерий Вальда) и его свойства

Построение статистического критерия при фиксированном объеме выборки сводится в конечном счете к разбиению области возможных значений критической статистики на две части: область правдоподобных и область неправдоподобных (в условиях справедливости проверяемой гипотезы ) значений . При попадании конкретного значения в область неправдоподобных значений принимается решение об отклонении проверяемой гипотезы.

Последовательный критерий, т.е. критерий, основанный на последовательной схеме наблюдений, построен по той же логической схеме с одним отличием: последовательно для каждого фиксированного объема выборки область возможных значений критической статистики разбивается на три непересекающиеся части: область правдоподобных, область неправдоподобных и область сомнительных (в условиях справедливости проверяемой гипотезы ) значений, т.е.

, .

На каждом -м шаге последовательной схемы наблюдений, т.е. при наличии наблюдений , , решение принимается по следующему правилу:

Если , то проверяемая гипотеза принимается;

Если 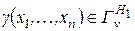, то проверяемая гипотеза отвергается (или принимается некоторая альтернатива );

Если , то окончательный вывод откладывается и производиться следующее -е наблюдение (поэтому область иногда называют областью неопределенности или областью продолжения наблюдений).

Таким образом, для того чтобы иметь какой-то конкретный статистический критерий, надо конкретизировать: а) тип проверяемой гипотезы; б) способ построения критической статистики ; в) способ построения областей , и по заданным (требуемым) значениям характеристик точности критерия.

В качестве конкретного примера последовательного критерия рассмотрим критерий отношения правдоподобия Вальда, с помощью которого определяют различие двух простых гипотез

: выборка извлечена из генеральной совокупности ;

: выборка извлечена из генеральной совокупности ;

Критическая статистика этого критерия для последовательности независимых наблюдений определяется соотношением

, .

Области правдоподобных , неправдоподобных и сомнительных , в условиях справедливости гипотезы , значений критической статистики приближенно задаются соотношениями:

;

;

.

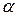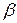Среди всех критериев, различающих эти гипотезы с ошибками первого и второго рода, не превосходящими заданных величин и , критерий Вальда требует наименьшего среднего числа наблюдений как в условиях справедливости гипотезы , так и в условиях справедливости гипотезы .

Исследования показали, что этот критерий примерно в два-четыре раза выгоднее (по затратам на наблюдения), чем наилучший из классических критериев – критерий отношения правдоподобия (критерий Неймана–Пирсона).