 |
Главная |
Критерий однородности Смирнова
|
из
5.00
|
Этот критерий предназначен для проверки гипотезы совпадения законов распределения вероятностей в двух или нескольких генеральных совокупностях по группированным выборкам, извлеченным из этих совокупностей, т.е. для проверки гипотез типа (2а). Пусть имеется 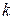 выборок
выборок
1-я: 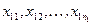 ;
;
2-я: 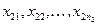 ;
;
…………………...;
k-я: 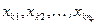 .
.
Причем разбиение диапазонов исследуемых случайных величин на интервалы группирования во всех выборках произведено одинаковым способом (при этом выбор общего размаха варьирования анализируемого признака во всех выборках определяется наименьшим из минимальных выборочных значений и наибольшим из максимальных выборочных значений). Таким образом, мы имеем 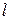 одних и тех же для всех выборок интервалов группирования и пусть
одних и тех же для всех выборок интервалов группирования и пусть  – количество элементов
– количество элементов 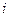 -й выборки, попавших в
-й выборки, попавших в 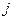 -й интервал
-й интервал 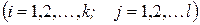 . В качестве критической статистики критерия используется величина
. В качестве критической статистики критерия используется величина
 , (5)
, (5)
где  – общее число элементов
– общее число элементов 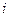 -й выборки,
-й выборки, 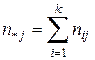 – общее (по всем выборкам) число выборочных данных, попавших в
– общее (по всем выборкам) число выборочных данных, попавших в 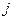 -й интервал группирования и
-й интервал группирования и 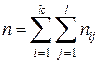 – суммарный (по всем выборкам) объем выборочных данных.
– суммарный (по всем выборкам) объем выборочных данных.
Смирновым было доказано, что при неограниченном росте объемов всех выборок и в условиях справедливости проверяемой гипотезы закон распределения вероятностей критической статистики (5) стремится к закону 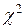 с
с 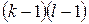 степенями свободы. Поэтому гипотеза отвергается, если
степенями свободы. Поэтому гипотеза отвергается, если 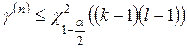 или
или  , и принимается при всех остальных значениях критической статистики
, и принимается при всех остальных значениях критической статистики 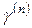 .
.
В частном случае двух выборок (т.е. 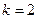 )
)
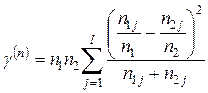 ,
,
и при условии справедливости гипотезы однородности она будет приблизительно распределена (при больших объемах  и
и 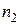 ) по закону
) по закону 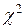 с
с 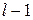 степенью свободы.
степенью свободы.
Пример.
Описанный метод проверки однородности относится к непараметрическим критериям, так как используемая в нем критическая статистика никак не зависит от наших предположений относительно параметрического общего вида анализируемых распределений (или, как иногда говорят, «свободна от распределения»). В этом его преимущество перед параметрическими критериями. Однако его реализация требует достаточно больших объемов анализируемых выборок (по крайней мере, они должны содержать по несколько десятков наблюдений).
Критерий Стьюдента (  -критерий)
-критерий)
Этот критерий предназначен для проверки гипотезы однородности средних значений в двух нормальных генеральных совокупностях, имеющих одинаковую (хотя и неизвестную) дисперсию 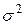 . В качестве критической статистики в данном критерии используется величина
. В качестве критической статистики в данном критерии используется величина
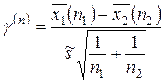 ,
,
где 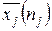 и
и  – соответственно выборочные средние и выборочные дисперсии, построенные по
– соответственно выборочные средние и выборочные дисперсии, построенные по  -й выборке
-й выборке  , а
, а 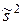 вычисляется по выборочным дисперсиям по формуле
вычисляется по выборочным дисперсиям по формуле
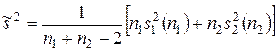 .
.
Вычисленная таким образом критическая статистика подчиняется распределению Стьюдента с 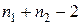 степенями свободы. Поэтому, определив из таблиц (при заданном уровне значимости критерия
степенями свободы. Поэтому, определив из таблиц (при заданном уровне значимости критерия 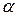 )
)  -ную точку
-ную точку 
 -распределения с
-распределения с 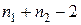 степенями свободы, мы принимаем решение об отклонении гипотезы однородности, если окажется, что
степенями свободы, мы принимаем решение об отклонении гипотезы однородности, если окажется, что 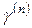 по абсолютной величине превзойдет значение
по абсолютной величине превзойдет значение  .
.
Замечание. Слишком большое значение статистики, т.е. такое, при котором отвергается проверяемая гипотеза однородности, может быть следствием как статистически значимого расхождения выборочных средних (т.е. невыполнение гипотезы (2б)), так и статистически значимого расхождения дисперсий (т.е. невыполнение гипотезы (2в)). Поэтому если мы хотим понять, за счет чего обнаружилась неоднородность анализируемых выборок, то необходимо произвести дополнительную проверку однородности дисперсий, т.е. гипотезы (2в). Эта же задача может являться и самостоятельной целью исследования.
 -критерий однородности дисперсий
-критерий однородности дисперсий
Этот критерий предназначен для проверки гипотезы однородности дисперсий в двух нормальных генеральных совокупностях. Он основан на использовании критической статистики
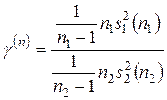 .
.
В условиях справедливости гипотезы (2в) эта критическая статистика должна подчиняться  -распределению с числами степеней свободы числителя и знаменателя, равными соответственно
-распределению с числами степеней свободы числителя и знаменателя, равными соответственно 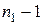 и
и 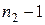 . Поэтому при заданном уровне значимости критерия
. Поэтому при заданном уровне значимости критерия 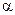 определяем
определяем 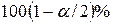 -ную и
-ную и 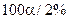 -ную точки
-ную точки 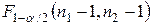 и
и 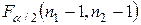 . Если окажется, что
. Если окажется, что
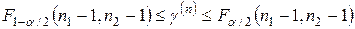 ,
,
то гипотеза однородности дисперсий не отвергается (и отвергается при всех других значениях критической статистики).
Пример.
|
из
5.00
|
Обсуждение в статье: Критерий однородности Смирнова |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

