 |
Главная |
Принцип тождественности. Фермионы и бозоны
|
из
5.00
|
Важнейшим принципом, используемым при описании квантовых газов, является принцип тождественности, т.е. принцип неразличимости одинаковых по природе (обладающих одинаковой массой, зарядом, спином) микрочастиц, входящих в состав квантового газа.
Этот принцип означает в случае квантовых объектов, что обмен местами двух частиц, находящихся в состояниях, описываемых волновыми функциями Y1 и Y2 , не является "физическим событием", т.е. не изменяет состояние системы. Если, например, после взаимодействия (столкновения) двух таких тождественных частиц мы обнаруживаем одну из них вблизи некоторой точки пространства, то не существует возможности указать, какая именно из них туда попала.
В простейшем случае системы двух слабовзаимодействующих микрочастиц частицы "1" и "2" можно считать свободными и описывать волновыми функциями, представляющими плоские волны:

с волновыми векторами  и
и  . Предположим, что частицы имеют одинаковые энергии:
. Предположим, что частицы имеют одинаковые энергии:  , т.е.
, т.е.  и примерно одинаковое направление движения в точки
и примерно одинаковое направление движения в точки 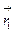 и
и  , расположенные близко друг к другу. Поскольку вероятность одновременного обнаружения невзаимодействующих частиц "1" и "2" вблизи точек
, расположенные близко друг к другу. Поскольку вероятность одновременного обнаружения невзаимодействующих частиц "1" и "2" вблизи точек 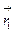 и
и  , соответственно, равна произведению независимых вероятностей, то такая двухчастичная система будет описываться волновой функцией
, соответственно, равна произведению независимых вероятностей, то такая двухчастичная система будет описываться волновой функцией
 .
.
Если частицы тождественны, то полная волновая функция, описывающая вероятность одновременного обнаружения их в точках 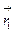 и
и  , должна быть определена как суперпозиция волновых функций, определяющих эти два тождественных состояния. При этом интерферирующие волновые функции, могут иметь некоторый сдвиг по фазе, поскольку физически измерима только вероятность обнаружения микрочастиц в указанных точках. Таким образом,
, должна быть определена как суперпозиция волновых функций, определяющих эти два тождественных состояния. При этом интерферирующие волновые функции, могут иметь некоторый сдвиг по фазе, поскольку физически измерима только вероятность обнаружения микрочастиц в указанных точках. Таким образом,
 ,
,
откуда следует, что
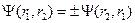 . (3.4)
. (3.4)
Волновая функция, удовлетворяющая этому равенству с положительным знаком, называется симметричной, а с отрицательным знаком – антисимметричной.
Знак соотношения (3.4) определен фазовым множителем. Преобразуем соотношение (3.4) к виду:
 .
.
Тогда знаку "плюс" соответствует  , а знаку "минус"
, а знаку "минус"  , т.е. в первом случае Y-функции тождественных частиц интерферируют в фазе, а во втором – в противофазе.
, т.е. в первом случае Y-функции тождественных частиц интерферируют в фазе, а во втором – в противофазе.
Микрочастицы, для которых волновые функции тождественных состояний, интерферируют в фазе, т.е. являются симметричными, называются бозонами.
Микрочастицы, для которых волновые функции тождественных состояний, интерферируют в противофазе, т.е. являются антисимметричными, называются фермионами.
При этом оказывается, что фермионы обладают полуцелым спином, т.е. проекция спина на выделенное направление  , а бозоны - целым спином,
, а бозоны - целым спином,  . К фермионам относятся: электрон, протон, нейтрон; к бозонам - фотон, фонон, a-частица, а также ядра, состоящие из четного числа нуклонов. (Спин – это собственный механический момент микрочастицы.)
. К фермионам относятся: электрон, протон, нейтрон; к бозонам - фотон, фонон, a-частица, а также ядра, состоящие из четного числа нуклонов. (Спин – это собственный механический момент микрочастицы.)
Фермионы и бозоны вследствиеих различного поведения в коллективе себе подобных микрочастиц подчиняются разным квантовым статистикам, т.е. функции распределения их по квантовым состояниям различны. Квантовое состояние микрообъекта однозначно определяется видом волновой функции (с учетом спина), которая, в свою очередь, однозначно определяет его динамические параметры через соответствующие квантовые числа. В случае идеального квантового газа, в котором волновые функции микрочастиц можно рассматривать как плоские (или сферические) волны  , квантовое состояние удобно задавать набором проекций
, квантовое состояние удобно задавать набором проекций 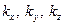 волнового вектора (
волнового вектора (  ) или импульса
) или импульса  , которые определяют величину полной энергии. Таким образом, в дальнейшем под выражением "попасть в одно и то же квантовое состояние" мы будем понимать "обладать одним и тем же набором проекций импульса" и соответственно одинаковой энергией, а также одинаковой проекцией спина.
, которые определяют величину полной энергии. Таким образом, в дальнейшем под выражением "попасть в одно и то же квантовое состояние" мы будем понимать "обладать одним и тем же набором проекций импульса" и соответственно одинаковой энергией, а также одинаковой проекцией спина.
Волновая функция системы двух тождественных частиц, как уже отмечалось, есть суперпозиция волновых функций, описывающих тождественные состояния, отличающиесяих перестановкой. Рассмотрим "попадание" двух частиц в одинаковое квантовое состояние. Если бы частицы были неразличимы, вероятность обнаружения в данной точке (в данном состоянии) одной из них не зависела бы от того, есть ли там другая частица. В случае же тождественных бозонов вероятность обнаружения в данном квантовом состоянии одного из них в присутствии другого увеличивается, т.е. присутствие одной частицы в данном состоянии влияет на другую, увеличивая вероятность "попадания" ее в это состояние в два раза по сравнению с тем случаем, когда состояние не занято. Другими словами, между тождественными частицами возникает некоторое взаимодействие, которое называется обменным. Оно не имеет аналогов в классической физике и формально вводится в квантово-механические соотношения через потенциал взаимодействия, характеризующий "статистическое притяжение" бозонов.
В случае фермионов вероятность обнаружения в данном квантовом состоянии одного из них в присутствии другого равна нулю, т.е. в данном квантовом состоянии в данной точке нельзя обнаружить одновременно два фермиона (подразумевается, что они обладают одинаково направленными спинами, т.е. состояния полностью тождественны). Другими словами, полученный для фермионов результат означает, что они подчиняются
принципу Паули: в данном квантовом состоянии в данный момент времени в данной точке может находиться не более одного фермиона.
По аналогии со "статистическим притяжением" бозонов это можно рассматривать,каксвоеобразное "статистическое отталкивание" фермионов.
Распределение частиц по квантовым состояниям. Виды квантовых статистик
Основной задачей квантовой статистики является определение числа  частиц квантового газа, обладающих значениями энергии от
частиц квантового газа, обладающих значениями энергии от  до
до  . Очевидно, что
. Очевидно, что  будет равно произведению числа состояний в
будет равно произведению числа состояний в  на среднее число частиц, находящихся в каждом из этих состояний.
на среднее число частиц, находящихся в каждом из этих состояний.
Обычно вводится функция распределения частиц по энергиям 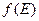 , которая и дает среднее число частиц в состояниях с энергией от
, которая и дает среднее число частиц в состояниях с энергией от  до
до  . Тогда
. Тогда
 . (3.5)
. (3.5)
Число частиц с данной энергией  и разными спинами учитывается множителем
и разными спинами учитывается множителем  в выражении для плотности состояний (3.3).
в выражении для плотности состояний (3.3).
Как следует из предыдущего рассмотрения характер заполнения квантового состояния фермионами и бозонами различен, что определяет различие в их функциях распределения. Для бозонов - это функция распределения Бозе-Эйнштейна (  ), а для фермионов - это функция распределения Ферми-Дирака (
), а для фермионов - это функция распределения Ферми-Дирака (  ).
).
· Квантовая статистика бозонов была создана в 1924-1925 гг. А.Эйнштейном и индийским физиком Ш.Бозе; квантовую статистику фермионов в 1925-1926 гг. независимо друг от друга разработали итальянский и английский физики-теоретики Э.Ферми и П.Дирак.
Для функций распределения Бозе-Эйнштейна и Ферми-Дирака имеем, соответственно, следующие выражения:
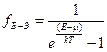 , (3.6)
, (3.6)
 (3.7)
(3.7)
где  - химический потенциал, равный изменению внутренней энергии системы при изменении числа частиц на единицу (в условиях постоянства объема и энтропии).
- химический потенциал, равный изменению внутренней энергии системы при изменении числа частиц на единицу (в условиях постоянства объема и энтропии).
Далее остановимся более подробно на каждом из двух типов квантовых газов.
Бозе–газ
В этом случае имеет место распределение Бозе-Эйнштейна:
 , (3.8)
, (3.8)
где  - среднее число частиц, находящихся в состоянии с номером
- среднее число частиц, находящихся в состоянии с номером 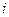 ,
,  – энергия частиц в этом состоянии.
– энергия частиц в этом состоянии.
 Значения химического потенциала
Значения химического потенциала  в распределении (3.8) не могут быть положительными, т.е.
в распределении (3.8) не могут быть положительными, т.е. 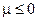 , ибо в противном случае при
, ибо в противном случае при  среднее число
среднее число  оказалось бы отрицательным.
оказалось бы отрицательным.
 График функции распределения Бозе-Эйнштейна в случае
График функции распределения Бозе-Эйнштейна в случае  для температуры
для температуры  представлен на рис. 3.5.
представлен на рис. 3.5.
Как видно из рисунка, с уменьшением энергии функция распределения Бозе-Эйнштейна стремиться к бесконечности, т.е. среднее число бозонов в квантовом состоянии быстро растёт. Поэтому можно сказать, что бозоны - “коллективисты”.
Интересный характер поведения имеет бозе-газ при  . Химический потенциал бозе-газа при
. Химический потенциал бозе-газа при  должен обращаться в нуль. В этом случае при приближении к абсолютному нулю числа частиц на квантовых уровнях
должен обращаться в нуль. В этом случае при приближении к абсолютному нулю числа частиц на квантовых уровнях  будут стремиться к нулю. Исключение составляют только частицы на нижнем квантовом уровне
будут стремиться к нулю. Исключение составляют только частицы на нижнем квантовом уровне  . Для числа частиц на энергетическом уровне
. Для числа частиц на энергетическом уровне  при
при  формула (3.8) приводит к неопределенному выражению
формула (3.8) приводит к неопределенному выражению  .
.
Таким образом, при приближении к абсолютному нулю бозе-частицы все более и более будут накапливаться на нижнем энергетическом уровне  и, наконец, все они окажутся на нем при
и, наконец, все они окажутся на нем при  .
.
Это явление получило название бозе-эйнштейновской конденсации. Разумеется, такая «конденсация» не имеет ничего общего с конденсацией пара в жидкость.
2) Ферми-газ
В случае ферми-газа имеет место распределения Ферми – Дирака:
 . (3.9)
. (3.9)
В отличие от (3.8), химический потенциал  в распределении (3.9) может иметь и положительное значение (в данном случае это не приводит к отрицательным значениям чисел
в распределении (3.9) может иметь и положительное значение (в данном случае это не приводит к отрицательным значениям чисел  ).
).
График функции распределения Ферми – Дирака 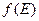 в случае
в случае  показан на рис. 3.6. При уменьшении энергии функция распределения Ферми-Дирака быстро принимает значение равное 1, т.е. среднее число фермионов в квантовом состоянии равно одному, что соответствует принципу Паули. Поэтому можно сказать, что фермионы - “индивидуалисты”.
показан на рис. 3.6. При уменьшении энергии функция распределения Ферми-Дирака быстро принимает значение равное 1, т.е. среднее число фермионов в квантовом состоянии равно одному, что соответствует принципу Паули. Поэтому можно сказать, что фермионы - “индивидуалисты”.

При абсолютном нуле температуры Т = 0

Это означает, что при Т = 0 частицы ферми-газа заполняют все квантовые состояния с энергиями 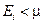 . Квантовые состояния с более высокими энергиями не заполнены. Говорят, что при Т = 0 ферми-газ находится в состоянии полного вырождения. Кривая, изображающая соответствующее распределение, вырождается в прямоугольник (рис. 3.6,б)
. Квантовые состояния с более высокими энергиями не заполнены. Говорят, что при Т = 0 ферми-газ находится в состоянии полного вырождения. Кривая, изображающая соответствующее распределение, вырождается в прямоугольник (рис. 3.6,б)
Таким образом, при Т = 0  совпадает с верхним заполненным электронным уровнем. Этот уровень называется уровнем Ферми или энергией Ферми
совпадает с верхним заполненным электронным уровнем. Этот уровень называется уровнем Ферми или энергией Ферми  . Поэтому функцию распределения (3.9) можно ещё записать в виде:
. Поэтому функцию распределения (3.9) можно ещё записать в виде:
 . (3.10)
. (3.10)
В заключение заметим, что функции распределения бозе-газа и ферми-газа отличаются только знаком перед единицей в знаменателе дроби, но этот знак приводит к принципиальным физическим различиям в области малых значений энергии, когда  сравнимо с
сравнимо с  .
.
В случае же больших энергий, когда  (что выполняется в области “хвоста” кривых распределения) единицей в знаменателе можно пренебречь. Тогда обе функции распределения по состояниям с различной энергией принимают вид:
(что выполняется в области “хвоста” кривых распределения) единицей в знаменателе можно пренебречь. Тогда обе функции распределения по состояниям с различной энергией принимают вид:
 Рис. 3.7
Рис. 3.7
|
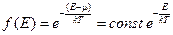 ,
,
т.е. переходят в классическое распределение Больцмана (см. рис. 3.7).
4. Внутренняя энергия твердого тела
|
из
5.00
|
Обсуждение в статье: Принцип тождественности. Фермионы и бозоны |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

