 |
Главная |
Выполнение расчетных заданий
|
из
5.00
|
1. Число символов алфавита m = 4. Вероятности появления символов равны соответственно p1 = 0,15; p2 = 0,4; p3 = 0,25; p4 = 0,2. Длительности символов t1 = 3с; t2 = 2с; t3 = 5с, t4 = 6с. Чему равна скорость передачи сообщений, составленных из таких символов?
2. Сообщения составлены из пяти качественных признаков (m = 5). Длительность элементарной посылки t = 20мс. Определить, чему равна скорость передачи сигналов и информации.
3. Определить пропускную способность бинарного канала связи, способного передавать 100 символов 0 или 1 в единицу времени, причем каждый из символов искажается (заменяется противоположным) с вероятностью р = 0,01.
4. Имеются источник информации с энтропией в единицу времени H(Х) = 100 дв.ед. и два канала связи; каждый из них может передавать в единицу времени 70 двоичных знаков (0 или 1); каждый двоичный знак заменяется противоположным с вероятностью р = 0,1. Требуется выяснить, достаточна ли пропускная способность этих каналов для передачи информации, поставляемой источником.
5. Чему равна пропускная способность симметричного канала, если источник вырабатывает сигналы со скоростью 2 знака в секунду, закодированные кодом с основанием m = 10, а вероятность ложного приема р = 0,3?
6. Сообщения составлены из алфавита Х = (х1, x2, x3). Вероятности появления символов алфавита 0,7; 0,2; 0,1 соответственно. Помехи в канале связи заданы следующей канальной матрицей:
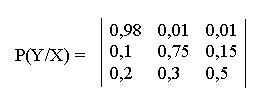
Определить скорость передачи информации, если время передачи одного символа t1 = 0,02с.
7. Чему раина пропускная способность канала связи, описанного канальной матрицей:

если известно, что на выходе источника сообщений символы вырабатываются со скоростью 100 знаков в секунду?
8. Определить максимально возможную скорость передачи информации по радиотехническому каналу связи пункта управления с телеуправляемой ракетой, если полоса пропускания канала связи равна 3 МГц, а минимальное отношение сигнал-шум по мощности в процессе наведения ракеты на цель равно 3.
9. Определить полосу пропускания канала передачи телевизионного черно-белого изображения с 5х105 элементами, 25 кадрами в секунду и 8 равновероятными градациями яркости для отношения P/N = 15 при условии, что изображение может принимать наиболее хаотичный вид «белого шума».
Отчет
Отчет должен быть оформлен в текстовом редакторе и содержать:
¾ наименование работы;
¾ цель работы;
¾ задание;
¾ последовательность выполнения работы;
¾ ответы на контрольные вопросы;
¾ вывод о проделанной работе.
Контрольные вопросы
1. Что такое пропускная способность канала передачи информации? Чем отличается пропускная способность от скорости передачи информации по каналу связи?
2. Чем отличается информационная скорость передачи от технической, и в каких единицах эти скорости измеряются?
3. Как изменяется пропускная способность дискретного канала связи при воздействии на канал помех.
4. Сформулируйте основную теорему Шеннона о кодировании для канала без помех.
5. Сформулируйте и поясните теорему Шеннона о кодировании для канала с помехами.
6. Приведите выражение пропускной способности для дискретного канала без помех и с помехами.
7. Сформулируйте и поясните теорему отсчетов (Котельникова)
8. Какие параметры влияют на объем сигнала.
9. От чего зависит пропускная способность непрерывного канала связи.
10. Назовите условия согласования источников информации с пропускной способностью непрерывных каналов связи.
11. Какова скорость отображения информации приемным устройством отображения информации.
Практическое занятие № 7
Тема программы: Смысл энтропии Шеннона.
Тема: Расчет вероятностей.
Цель: научиться вычислять вероятности событий (появление символов в сообщении) и рассчитывать энтропию.
Время выполнения: 2 часа
Оборудование: ПК.
Программное обеспечение: операционная система, калькулятор, текстовый редактор.
Теоретические основы
Количество информации по Хартли и Шеннону
Понятие количество информации отождествляется с понятием информация. Эти два понятия являются синонимами. Мера информации должна монотонно возрастать с увеличением длительности сообщения (сигнала), которую естественно измерять числом символов в дискретном сообщении и временем передачи в непрерывном случае. Кроме того, на содержание количества информации должны влиять и статистические характеристики, так как сигнал должен рассматриваться как случайный процесс.
При этом наложено ряд ограничений:
1. Рассматриваются только дискретные сообщения.
2. Множество различных сообщений конечно.
3. Символы, составляющие сообщения равновероятны и независимы.
Хартли впервые предложил в качестве меры количества информации принять логарифм числа возможных последовательностей символов.
I=log mk=log N (1)
К.Шеннон попытался снять те ограничения, которые наложил Хартли. На самом деле в рассмотренном выше случае равной вероятности и независимости символов при любом k все возможные сообщения оказываются также равновероятными, вероятность каждого из таких сообщений равна P=1/N. Тогда количество информации можно выразить через вероятности появления сообщений I=-log P.
В силу статистической независимости символов, вероятность сообщения длиной в k символов равна

Если i-й символ повторяется в данном сообщении ki раз, то 
так как при повторении i символа ki раз k уменьшается до m. Из теории вероятностей известно, что, при достаточно длинных сообщениях (большое число символов k) ki≈k·pi и тогда вероятность сообщений будет равняться 
Тогда окончательно получим
 (2)
(2)
Данное выражение называется формулой Шеннона для определения количества информации.
Формула Шеннона для количества информации на отдельный символ сообщения совпадает с энтропией. Тогда количество информации сообщения состоящего из k символов будет равняться I=k·H
Количество информации, как мера снятой неопределенности
При передаче сообщений, о какой либо системе происходит уменьшение неопределенности. Если о системе все известно, то нет смысла посылать сообщение. Количество информации измеряют уменьшением энтропии.
Количество информации, приобретаемое при полном выяснении состояния некоторой физической системы, равно энтропии этой системы:

Количество информации I - есть осредненное значение логарифма вероятности состояния. Тогда каждое отдельное слагаемое -log pi необходимо рассматривать как частную информацию, получаемую от отдельного сообщения, то есть
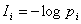
|
из
5.00
|
Обсуждение в статье: Выполнение расчетных заданий |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

