 |
Главная |
Практическая работа № 2
|
из
5.00
|
Тема:Вычисление комбинаторных объектов заданного типа
Цели работы:
1)научиться находить количество элементов в объединении нескольких множеств;
2) научиться вычислять число всевозможных комбинаторных объектов заданного типа.
Пояснения:
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок:
Pn = n!,
где n! = 1 * 2 * 3 ... n.
Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений:
 =
= 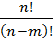
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний:

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
При решении задач комбинаторики используют следующие правила:
Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Оборудование, аппаратура, материалы и их характеристики:персональные компьютеры с лицензионным программным обеспечением; доска, маркеры; рабочие тетради; раздаточный материал.
Порядок выполнения работы:
Студенты получают задания по вариантам. Метод решения выбирается студентами самостоятельно и зависит от приобретенных в процессе обучения навыков. В процессе выполнения практической работы преподаватель проводит как групповые, так и индивидуальные консультации по вопросам дополнительного разъяснения отдельных понятий и аспектов изученных тем, задания и оформления отчета.
1. Решите задачу:
Из 100 студентов факультета программирования 42 посещают спортивные секции, 30 — занятия научного общества, а 28 — кружки художественной самодеятельности. На занятия научного общества и спортом успевают ходить 5 студентов, спортом и художественной самодеятельностью занимаются 10, наукой и художественной самодеятельностью — 8, а сразу все три увлечения имеют три студента.
Таблица 1 – Задание № 1
| № варианта | Исходные данные |
| Сколько студентов занимается только спортом? | |
| Сколько студентов не посещают ни одно из этих объединений по интересам? | |
| Сколько студентов занимаются или спортом или художественной самодеятельностью, но не в НО? | |
| Сколько студентов занимаются либо спортом, либо художественной самодеятельностью, но не в НО? | |
| Сколько студентов занимаются или в НО или художественной самодеятельностью, но не спортом? |
В результате социологического опроса студентов факультета программирования о занятиях в свободное от уроков время выяснилось, что из 100 человек: 18 — любят только читать книги; 21 — читают книги, но не ходят в театр; 7 — читают книги и посещают театр; 28 – читают книги; 47 — ходят на дискотеки; 9 — посещают театр и дискотеки; 2 – любят читать книги, ходят на дискотеки и посещают театр; 13 — лежат на диване перед телевизором, занимаются только просмотром всех возможных каналов телевидения.
Таблица 2 – Задание № 1
| № варианта | Исходные данные |
| Сколько студентов любят ходить в театр? | |
| Сколько студентов читают книги, посещают театр, но не дискотеки? | |
| Сколько студентов посещают либо дискотеки, либо театр? | |
| Сколько студентов предпочитают только дискотеки? | |
| Сколько студентов, посещая дискотеки и театр, не любят читать книги? |
2. Решите задачи:
Таблица 3 – Задание № 2
| № варианта | Исходные данные |
| 1. Метранпаж выбирает из ящика, в котором лежат (каждой по одной) литеры букв русского, латинского, греческого алфавитов, цифр и знаков препинания, одну литеру. Сколькими способами он может это сделать? 2. Сколькими способами 12 одинаковых монет достоинством в 1 рубль можно разложить по пяти различным пакетам, если ни один из пакетов не должен быть пустым? | |
| 1. В книжном шкафу стоят девятитомник Ф. Купера, восьмитомник В. Скотта, шеститомник М. Рида и пятитомник Р. Киплинга. Сережа выбирает одну книгу для внеклассного чтения. Сколькими способами он может это сделать? 2. Сережа утверждает, что число трехбуквенных слов, которые можно образовать из букв, составляющих слово гипотенуза, равно числу всех возможных перестановок букв, составляющих слово призма. Прав ли Сережа? | |
| 1. Три дороги соединяют города А и В, четыре дороги соединяют В и С. Сколькими способами можно совершить поездку из А в С через В и вернутся обратно в А через В? 2. Елена шьет разноцветные флаги. Сколькими способами она может составить трехцветный полосатый флаг (с заданным положением полос), если имеется материал пяти различных цветов и одна из полос должна быть красной (красный – среди имеющихся цветов)? | |
| 1. В корзине лежат 12 яблок и 10 апельсинов. Сережа выбирает из нее яблоко или апельсин, после чего Елена берет и яблоко, и апельсин. В каком случае Елена имеет большую свободу выбора: если Сережа взял яблоко или если он взял апельсин? 2. Сережа хочет отгадать, какие пять монет держит в руке Елена. Она располагает достаточным количеством монет достоинством в 1, 2, 5, 10, 50, 100 руб. Сколько может быть дано различных неверных ответов? | |
| 1. Из Киева до Чернигова можно добраться пароходом, поездом, автобусом и самолетом; из Чернигова до Новгорода – пароходом и автобусом. Сколькими способами можно осуществить путешествие по маршруту Киев – Чернигов – Новгород? 2. В железнодорожном вагоне десять мест расположены по ходу поезда и десять – против хода поезда. Сколькими способами можно посадить в вагон восемь пассажиров, если двое отказываются сидеть лицом по ходу поезда, а трое – лицом против хода поезда? | |
| 1. У англичан принято давать детям несколько имен. Сколькими способами можно назвать ребенка, если общее число имен равно 300, а ему дают не более трех имен? 2. Трое юношей и две девушки выбирают место работы. В городе есть три завода, где требуется рабочие в литейные цеха (берут лишь мужчин), две ткацкие фабрики (приглашаются женщины) и две фабрики, где требуются и мужчины, и женщины. Сколькими способами они могут распределиться между этими предприятиями? | |
| 1. Серийные номера составляются из одной, двух или трех букв и четырех цифр. Найдите число таких номеров, если используются все 33 буквы русского алфавита? 2. В селении проживают 2000 жителей. Доказать. Что по крайней мере двое из них имеют одинаковые инициалы. | |
| 1. Городской совет состоит из мэра и шести старейшин. Сколько различных комиссий из четырех членов можно сформировать из членов городского совета, если мэр города входит в каждую комиссию? 2. Сколькими способами можно разложить девять книг в четыре бандероли по две книги и в одну бандероль – одну книгу? | |
| 1. Городской совет состоит из мэра и шести старейшин. Сколько различных комиссий из четырех членов можно сформировать из членов городского совета, если мэр города не входит ни в одну из комиссий? 2. Ювелиру принесли пять одинаковых изумрудов, шесть одинаковых рубинов и семь одинаковых сапфиров. Сколько различных браслетов (из всех 18 камней) может сделать ювелир? | |
| 1. Елена шьет разноцветные флаги. Сколькими способами она может составить трехцветный полосатый флаг (с заданным положением полос), если имеется материал пяти различных цветов? 2. Для премий на математической олимпиаде выделено три экземпляра одной книги, два экземпляра другой и один экземпляр третьей книги. Сколькими способами могут быть вручены премии, если в олимпиаде участвовало 20 человек и никому не дают двух экземпляров одной и той же книги, но могут быть вручены две или три различные книги? |
3. Для xÎN решите уравнения:
Таблица 4 – Задание № 3
| № Варианта | Исходные данные |
 =30 =30
| |
5 
| |

| |

| |
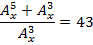
| |
12 
| |

| |

| |

| |

|
Требования к отчету: Отчет должен содержать:
- название практической работы;
- формулировку цели работы;
- краткие теоретические сведения по теме работы в виде таблиц, графиков, диаграмм, схем, рисунков и формул;
- результаты решения заданий;
- выводы по работе;
- краткие письменные ответы на контрольные вопросы.
Текст отчета набирается на компьютере. Допускается тип шрифта Times New Roman, размер 12 – 14, межстрочный 1,5 интервал, выравнивание текста по ширине странице, абзацный отступ 1,25.
Контрольные вопросы:
1) Что такое комбинаторика и для чего она нужна?
2) В чем отличие сочетаний от размещений?
3) Запишите формулу для вычисления числа сочетаний элементов, используемую в формуле бинома Ньютона.
Учебная и специальная литература:
1) Спирина М.С., Спирин В.В. Дискретная математика: Учебник. – М.: Издательский центр «Академия», 2009. – 370 с.
2) Игошин В.И. Задачи и упражнения по математической логике и теории алгоритмов: учеб. пособие для высш. учеб. заведений. – М.: Издательский центр «Академия», 2009. – 304 с.
3) Тишин В.В. Дискретная математика в примерах и задачах. – СПб.: БХВ – Петербург, 2008. – 352 с.
|
из
5.00
|
Обсуждение в статье: Практическая работа № 2 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

