Метод Гаусса с выбором главного элемента

Метод Гаусса относится к точным методам решения. Если исключить погрешности округления при вычислениях (использовать обыкновенные дроби), то за конечное число операций можно получить точное решение.

Анализ алгоритма решения показывает, что точность определяется значениями коэффициентов, расположенных на главной диагонали , которые называют ведущимиэлементами. На каждом шаге прямого хода предполагалось, что .Если это не так, то в качестве ведущего элемента можно использовать любой другой ненулевой коэффициент поменяв местами строки или столбцы матрицы. Однако если он окажется малым то после деления на этот элемент и последующего вычитания возникают большие погрешности округления. Чтобы избежать этого, на каждом этапе строки и столбцы переставляют так, чтобы на главной диагонали оказался наибольший по модулю элемент. Поскольку одновременный перебор строк и столбцов увеличивает количество операций и усложняет алгоритм, то обычно перебирают только строки. Найденный элемент, наибольший по модулю называют главным. В этом состоит суть метода Гаусса с выбором главного элемента.

Метод имеет малые погрешности округления при условии если матрица системы хорошо обусловлена. Матрица 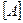называется плохо обусловленной, если малые изменения её элементов приводят к существенным изменениям элементов обратной матрицы . Произведение ведущих элементов равно определителю системы:

.

Откуда следует, что если система имеет решение - , то всегда можно найти ведущие элементы отличные от нуля и, следовательно, найти решение методом Гаусса с выбором главного элемента.

Метод Гаусса с выбором главного элемента надежен, прост и наиболее выгоден для систем ЛАУ с плотно заполненной матрицей.

Численные методы решения нелинейных и трансцендентных уравнений

Метод простой итерации

Система уравнений приведена к виду: X = G(X)

Если она задана в виде: , то преобразуем её, добавляя X к левой и правой частям.

X = F(X)+X.

В этом случае решение ищется по следующей итерационной формуле:

X_k = G(X_k-1).

Итерации прекращаются, когда ║X_k-X_k-1 ║≤ ε₁,

ε₁ – заданная погрешность решения.

Не всегда имеет место сходимость найденного решения к точному. Для того, чтобы сходимость имела место необходимо выполнение условия:

│∂G/∂Х│< 1.

Метод простой итерации является методом первого порядка, т.е.

║Х_к – Х^*║ ≤ с║Х_к-1 – Х^*║, где с – постоянная величина.

Метод Ньютона

Система нелинейных уравнений может быть записана виде:

F(X) = 0

f₁(x) = 0

f₂(x) = 0

………..

f_n(x) = 0

Х = (х₁; х₂; …; х_n)

Мы линеаризуем эту функцию в точке Х_к-1 , т.е. приведем к линейному виду.

Для этого раскладываем в ряд Тейлора.

,

где X_k= X_k-1+ ∆X_k .

∂f₁/∂x₁; ∂f₁/∂x₂; ….∂f₁/ ∂x_n

∂f₂/∂x₁; ∂f₂/∂x₂;….∂f₂/∂x_n;

∂F/∂X = ………………………………… – матрица первых

производных.

∂f_n/∂x₁; ∂f_n/∂x₂;…..∂f_n/∂x_n

Итерационный процесс заканчивается, когда ║∆X_k ║≤ ε₁

║ F(X_k ) ║≤ ε_2,

где норма вектора отождествляется с его длиной:

║А║ = √ А₁² + А₂² + …. +А_n²,

А= (А₁, А₂, …А_n)

Недостатком метода является то, что не всегда имеет место сходимость решения. Если имеется сходимость, то она носит квадратичный характер, т.е.

║Х_к – Х_к-1║²≤║Х_к – Х^*║,

где Х^* - точное решение.

Для линейной системы уравнений решение находится за одну итерацию.