Синтез схемы двоичного сумматора по модулю 4 с использованием алгоритмов декомпозиции

 

Рассмотрим реализацию алгоритмов многоуровневой декомпозиции на примере синтеза схемы двоичного сумматора по модулю 4. Синтезируемая схема имеет пять входов и три выхода (рис. 2.16).

 

Рис. 2.16

 

и – суммируемые цифры, принимающие значения 0, 1, 2, 3,

– результат операции суммирования, также принимающий значения 0, 1, 2, 3,

и входной и выходной сигналы переноса, принимающие значения «1» или «0» в зависимости от того, есть перенос или нет.

Сложность исходной схемы бит.

 

Абстрактный синтез.

В процессе решения задачи абстрактного синтеза построим числовую последовательность синтезируемой схемы.

Допустим 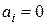, последовательно принимает значения 0, 1, 2, 3, а или 1 (всего восемь значений). Результат суммирования указанных чисел находится на пересечении соответствующих строк и столбцов. Во второй строке , также принимает значения от 0 до 3, а или 1 и т.д. до значения .

 

Числовая (логическая) последовательность синтезируемого сумматора имеет вид строки, состоящей из 32-х элементов :

. (2.16)

 

Структурный синтез

 

Так как схема имеет три выхода, попытаемся выделить параллельный блок. Для этого проверим наличие существенной или фиктивной зависимости выходных функций сумматора от входных аргументов. Присвоим входным переменным весовые коэффициенты, равные степени 2 (рис. 2.16) и построим матрицы разложения числовой последовательности синтезируемого сумматора по всем входным переменным (см. разд. 2.2.3):

;

;

;

;

.

Результаты проверки заносятся в специальную таблицу, строки которой отмечены именами выходов, а столбцы – весами входных переменных (табл. 2.3).

 

Таблица 2.3

 

 

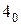
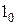
Заполнение каждого из столбцов указанной таблицы производится по следующему алгоритму:

1) для построенной выше матрицы разложения по старшей входной переменной ( ) элементы её первого столбца поразрядно (в двоичном представлении) суммируются по модулю два и полученное число заносится в столбец таблицы, соответствующий переменной, по которой проводилось разложение ( ). Единичные разряды полученного числа отмечают те выходы, которые существенно зависят от рассматриваемого входа;

2) операция суммирования выполняется над элементами второго столбца матрицы разложения, и полученная сумма объединяется по «ИЛИ» с уже записанным в соответствующий столбец таблицы числом;

3) процедура повторяется для всех последующих столбцов матрицы разложения до тех пор, пока не окажутся заполненными единицами все строки рассматриваемого столбца таблицы;

4) пункты 1 – 3 повторяются для всех остальных матриц разложения и таким же образом заполняются оставшиеся столбцы таблицы.

Если после просмотра всех столбцов всех матриц разложения в какой-либо строке таблицы остался символ «0», то это означает, что соответствующий выход зависит фиктивно от рассматриваемой входной переменной.

Построенная таким образом таблица позволяет выбрать группу выходов устройства, которые зависят не от всех входов. В рассматриваемом примере выход фиктивно зависит от входных переменных с весовыми коэффициентами и .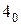

Схема, получаемая в результате параллельной декомпозиции синтезируемого устройства, представлена на рис. 2.17.

 

 

Рис. 2.17

Для определения числовой последовательности блока 2 из последовательности устройства (2.16) сначала выделяется двоичная последовательность младшего выхода (см. разд. 2.2.9):

.

А затем из неё исключаются фиктивные переменные, для чего необходимо построить матрицу разложения по соответствующим входным переменным (см. разд. 2.2.8):

(2.17)

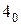В матрице (2.17) содержатся четыре одинаковые строки, что ещё раз подтверждает фиктивную зависимость числовой последовательности от входных переменных и . Числовой последовательностью блока 2 является строка матрицы (2.17) – .

Числовая последовательность блока 1, выходы которого существенно зависят от всех входных переменных, получается из исходной числовой последовательности путём исключения двоичной последовательности, соответствующей выходам второго блока. Для этого необходимо каждый элемент последовательности (2.16) разделить на два и взять целую часть от деления:

.

Сложность схемы после разделения будет составлять

бита.

Далее, в соответствии с приведённым выше алгоритмом структурного синтеза КЛС, из блока 1 попытаемся выделить последовательный блок с теми же входами, которые относятся к блоку 2. Для этого необходимо числовую последовательность блока 1 разложить в матрицу по входным переменным , , 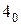, 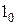которые являются существенными для блока 2:

(2.18)

По вертикали в матрице (2.18) изменяют свои значения выделенные входные переменные, относящиеся к старшему блоку (блок 3 на рис. 2.18), а по горизонтали – те переменные, которые не вошли в старший блок. Если два каких-либо набора значений входных переменных старшего блока неразличимы, то они неразличимы при любых значениях, не вошедших в этот блок переменных. Поэтому неразличимые комбинации переменных старшего блока будут давать в матрице одинаковые строки.

В матрице (2.18) две различных строки из восьми, поэтому из блока 1 можно выделить последовательный блок 3 с тремя входами и одним выходом (рис. 2.18).

 

 

Рис. 2.18

Сложность схемы после разделения:

бита.

Для определения последовательности блока 3 следует закодировать строки матрицы (3) по элементам первого столбца – .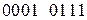

Для определения последовательности блока 4 строится сокращённая матрица разложения, которая образуется путём исключения из матрицы (2.18) повторяющихся строк:

Последовательность блока 4 получается развёртыванием по столбцам сокращённой матрицы разложения – .

Объединим параллельный блок 2 с последовательным блоком 3, поскольку эти блоки зависят от одних и тех же входных переменных. Выход последовательного блока будем считать старшим, поэтому при выполнении указанной операции необходимо каждый элемент последовательности блока 3 умножить на два и прибавить к результату соответствующий элемент параллельного блока 2 – . Результирующая схема представлена на рис. 2.19.

 

 

Рис. 2.19

 

Оба блока на рис. 2.19 имеют одинаковые последовательности ( ) и представляют собой двоичные сумматоры. Сложность схемы в результате объединения блоков 2 и 3 не увеличилась.

Дальнейший процесс декомпозиции целесообразно рассматривать для одного из блоков, поскольку они характеризуются одинаковыми числовыми последовательностями. Для входов двоичного сумматора необходимо ввести новые обозначения, совпадающие с их весовыми коэффициентам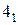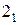и – , и 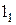(рис. 2.19). Индекс 1 в данном случае говорит о том, что эти обозначения относятся к блоку первого яруса схемы.

Для оценки возможности проведения параллельной декомпозиции построим матрицы разложения числовой последовательности двоичного сумматора по каждой входной переменной:

.

По построенным матрицам заполняется табл. 2.4, которая свидетельствует о существенной зависимости выходов двоичного сумматора от всех его входов.

 

 

Таблица 2.4

 

 

Для оценки возможности проведения последовательной декомпозиции строятся матрицы разложения числовой последовательности двоичного сумматора по всем возможным парам входных переменных:

В матрицах разложения по три различимых строки из четырёх, и поэтому из двоичного сумматора нельзя выделить последовательный блок.

На этом этап декомпозиции двоичного сумматора по модулю 4 заканчивается, поскольку дальнейшее разделение синтезируемой схемы с учётом критерия уменьшения сложности невозможно. Результирующая схема рассматриваемого комбинационного устройства представлена на рис. 2.20.

 

 

Рис. 2.20. Схема двоичного сумматора по модулю 4

 

Анализ синтезированной схемы

 

Чтобы убедиться в правильности результатов синтеза, а также в качестве примера проанализируем блок-схему двухразрядного двоичного сумматора, представленную на рис. 2.20. Каждый разряд двоичного сумматора характеризуется следующей собственной числовой последовательностью:

. (2.19)

К первому ярусу относится блок номер 1. На его входы поступают переменные , и 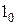. При выполнении процедуры последовательного счёта начиная с 0 переменная чередует свои значения через восемь элементов (восемь нулей, затем восемь единиц и т. д.), переменная чередует свои значения через два элемента (00 11 00 11 и т. д.), а переменная 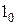– через один элемент (0 1 0 1 и т. д.). Общая длина интересующей нас последовательности составляет 32 элемента, поскольку анализируемая схема имеет пять входов. Выпишем одна под другой числовые последовательности, поступающие на входы 1-го блока:

(2.20)

С помощью двоичной матрицы (2.20) и собственной числовой последовательности блока 1 (2.19) построим реализуемую им числовую последовательность. Первый столбец двоичной матрицы (2.20) даёт нулевое значение индекса . На нулевом месте в (2.19) стоит «0». Поэтому в числовую последовательность записываем «0». Второй столбец двоичной матрицы даёт . В собственной числовой последовательности блока 1 на первом месте стоит «1», следовательно, в выходную последовательность далее записываем единицу. Следующий столбец (2.20) даёт значение индекса . На втором месте в (2.19) тоже стоит «1». Поэтому в выходную последовательность 1-го блока записываем ещё одну единицу. Следующий столбец двоичной матрицы даёт . В последовательности (2.19) этому значению индекса соответствует число «2». Записываем его в выходную последовательность блока. И так далее. В результате получаем следующую числовую последовательность, реализуемую блоком 1-го яруса:

. (2.21)

Удобно реализуемую блоком числовую последовательность строить прямо под двоичной матрицей входных последовательностей, отделив её чертой:

На старшие (верхние) входы блока 2-го яруса поступают входные переменные и 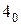, которые чередуют свои значения соответственно через 16 элементов (16 нулей, затем 16 единиц) и через четыре элемента (0000 1111 и т.д.). На младший (нижний) вход рассматриваемого блока поступает старший разряд полученной выше последовательности с выхода блока 1-го яруса. Поэтому разделим последовательность на старшую и младшую составляющие по весу 2 и старшую подадим на младший вход второго блока:

Выпишем одна под другой входные последовательности, поступающие не входы второго блока и определим состояния выходов в соответствии с его собственной числовой последовательностью – :

Два старших выхода анализируемого устройства связаны с выходами блока 2, а младший выход устройства – с выходом блока 1. Поэтому, результирующая последовательность исследуемой схемы получается в результате объединения последовательности (два старших разряда) и младшего разряда последовательности :

Полученная в результате анализа выходная последовательность полностью совпадает с исходной логической последовательностью, что доказывает правильность функционирования представленной на рис. 2.20 схемы.