Нормальная линейная регрессионная модель с одной переменной. Метод наименьших квадратов (МНК) для линейной парной регрессии

Простая парная регрессия представляет собой модель, где среднее значение зависимой переменной У рассматривается как функция одной независимой переменной Х: 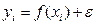. Теоретические значения параметров будем обозначать 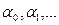; оценки этих параметров, полученных по выборке – 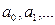, 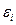– случайные величины, 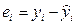– остаток регрессии. , , .

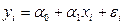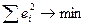Идея МНК заключается в минимизации суммы квадратов остатков.

Случайная величина включает в себя влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения.

Выбор вида функциональной зависимости можно провести следующими методами:

1) аналитический, т.е. исходя из теории изучаемой взаимосвязи;

2) графический – на основе корреляционного поля (диаграммы рассеяния);

3) экспериментально – построив несколько вариантов уравнения регрессии и выбрав лучший по показателям качества.

Принято считать, что число наблюдений должно в 6-7 раз превышать число рассчитываемых параметров.

Модель линейной парной регрессии.Общий вид: 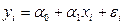, где х – неслучайная величина, у и - случайные величины. При этом x – экзогенная переменная, y – эндогенная. Выборочное уравнение регрессии: , где 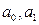- оценки параметров 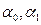. Неизвестные значения 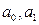определяются с помощью методы наименьших квадратов.

Не приводя доказательств, пропишем лишь формулы, для нахождения оценок параметров:

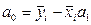
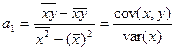
Линия регрессии будет проходить через точку 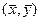и будут выполняться равенства:

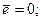
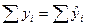. Коэффициент а₁ – угловой коэффициент регрессии, показывает на сколько единиц в среднем изменится переменная y при изменении независимой переменной x на единицу. Коэффициент а₀ дает прогнозируемое значение y при x = 0, часто не имеет экономической интерпретации.

Статистическая значимость коэффициентов регрессии также определяется с помощью t-критерия.

Показатели общего качества уравнения регрессии:

1. коэффициент детерминации R² – отношение, характеризующее долю вариации зависимой переменной, объясненную с помощью уравнения регрессии: . Чем ближе данная величина к единице, тем больше уравнение регрессии объясняет поведение фактических значений y.

Для парной линейной регрессии коэффициент детерминации есть квадрат коэффициента линейной парной корреляции: 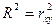. Значимость коэффициента детерминации означает значимость уравнения регрессии в целом и проверяется с помощью F – критерия Фишера:

Н₀: R² =0 – уравнение регрессии незначимо;

H₁: R² ≠0 – уравнение регрессии значимо.

. Величина имеет распределение Фишера с числом степеней свободы: 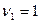, 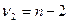. Если > 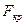=> Н₁ , иначе – Н₀ .

2. стандартная ошибка уравнения регрессии 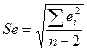. Обычно 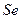сравнивают с (среднеквадратичным отклонением у). Если > 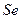, то использование модели регрессии целесообразно.

3. стандартная ошибка аппроксимации 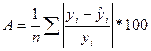для значимости уравнения регрессии должна принимать значения А ≤ 10-15%.