 |
Главная |
Некоторые правила алгебры комплексных чисел
|
из
5.00
|
Комплексным числом называется число вида
 ,
,
где 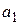 =
= 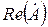 – вещественная часть комплексного числа;
– вещественная часть комплексного числа; 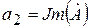 – коэффициент при его мнимой части;
– коэффициент при его мнимой части; 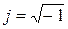 – мнимая единица.
– мнимая единица.
Приведенная запись представляет собой алгебраическую форму комплексного числа. Существуют также тригонометрическая и показательная формы:
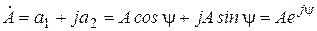 ,
,
где 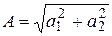 ;
;  ; е – основание натуральных логарифмов.
; е – основание натуральных логарифмов.
Величина А – модуль комплексного числа, 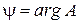 – его аргумент.
– его аргумент.
При складывании (вычитании) комплексных чисел удобно пользоваться их алгебраической формой, если  ,
, 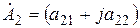 :
:
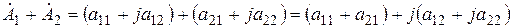 .
.
При умножении – показательной формой:
 ,
,
где 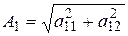 ;
;  ;
; 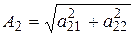 ;
;  .
.
Так же при делении:
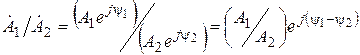 .
.
Если два комплексных числа ( 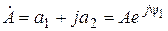 и
и 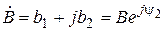 ) равны:
) равны: 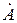 =
=  , то, следовательно, равны их вещественные и мнимые части, соответственно:
, то, следовательно, равны их вещественные и мнимые части, соответственно: 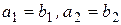 , кроме того, равны их модули –
, кроме того, равны их модули –  и аргументы –
и аргументы – 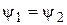 . Каждому комплексному числу
. Каждому комплексному числу 
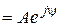 можно поставить в соответствие сопряженный комплекс
можно поставить в соответствие сопряженный комплекс 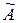 =
=  .
.
Геометрическим изображением комплексного числа 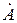 служит вектор в так называемой комплексной плоскости (рис.7), по оси абсцисс которой откладываются вещественные количества, по оси ординат – мнимые.
служит вектор в так называемой комплексной плоскости (рис.7), по оси абсцисс которой откладываются вещественные количества, по оси ординат – мнимые.

Рис. 7. Изображение комплексного числа вектором
Заметим, что часто для упрощения комплексное число в показательной форме  записывается в виде:
записывается в виде: 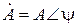 .
.
Синусоидальному току или напряжению заданной частоты ставится в соответствие его символическое изображение – комплексное число:
 Þ
Þ 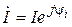 ,
,
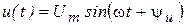 Þ
Þ 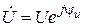 ,
,
где 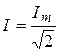 ,
,  – действующие значения тока и напряжения. Символические изображения синусоидальных величин в электротехнике обозначаются точками над соответствующими выражениями. Здесь употреблены так называемые действующие комплексы. Можно пользоваться также амплитудными комплексными изображениями:
– действующие значения тока и напряжения. Символические изображения синусоидальных величин в электротехнике обозначаются точками над соответствующими выражениями. Здесь употреблены так называемые действующие комплексы. Можно пользоваться также амплитудными комплексными изображениями:
 ,
, 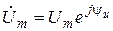 .
.
Заданные источники напряжения и тока также изображаются своими символами:
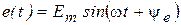 Þ
Þ 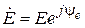 или
или  ,
,
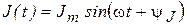 Þ
Þ  или
или  .
.
Такое соответствие между синусоидальными величинами известной частоты, с одной стороны, и комплексными числами, с другой стороны, базируется на том, что для характеристики синусоид необходимо знать их амплитуды и начальные фазы и каждое комплексное число несет в себе информацию в объеме двух количеств: вещественной и мнимой части или модуля и аргумента.
Решим обратную задачу. Пусть в результате преобразований получено изображение искомого тока в форме действующего комплекса 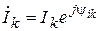 . Необходимо восстановить функцию времени, то есть записать, как ток зависит от времени. Восстанавливаем: ток изменяется по синусоидальному закону с заданной частотой
. Необходимо восстановить функцию времени, то есть записать, как ток зависит от времени. Восстанавливаем: ток изменяется по синусоидальному закону с заданной частотой 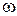 , амплитуда синусоиды равна модулю комплекса, умноженному на
, амплитуда синусоиды равна модулю комплекса, умноженному на  (например,
(например, 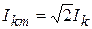 ), начальная фаза равна аргументу изображения
), начальная фаза равна аргументу изображения  , и, таким образом,
, и, таким образом, 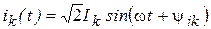 .
.
Главное достоинство символического метода состоит в том, что совокупность линейных интегро-дифференциальных уравнений, которыми в общем случае описывается линейная электрическая цепь произвольной сложности, сводится к системе алгебраических уравнений с комплексными коэффициентами и комплексными правыми частями. Искомые – символические изображения токов и напряжений.
|
из
5.00
|
Обсуждение в статье: Некоторые правила алгебры комплексных чисел |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

