 |
Главная |
Интегральный признак Коши
|
из
5.00
|
Предельный признак сравнения
Теорема
Пусть даны два ряда ∑  и ∑
и ∑  (к=1..
(к=1..  )такие что
)такие что  , тогда оба эти рядя либо сходятся либо расходятся одновременно(т е ведут себя одинаково)
, тогда оба эти рядя либо сходятся либо расходятся одновременно(т е ведут себя одинаково)
2.Признак Даламбера
Теорема
Пусть дан ряд с положительными членами  такой что
такой что 
1)если  то ряд сходится
то ряд сходится
2) если  то ряд расходится
то ряд расходится
3) если  неизвестно
неизвестно
Радикальный признак Коши
Теорема
Пусть дан ряд  такой что
такой что 
1) если  то ряд сходится
то ряд сходится
2) если  то ряд расходится
то ряд расходится
3) если  неизвестно
неизвестно
Интегральный признак Коши
Теорема
Пусть ф-ия f(x) определена непрерывна и ограничена на [1,+ 
тогда ряд  (
(  )и несобственный интеграл
)и несобственный интеграл  сходятся или расходятся одновременно
сходятся или расходятся одновременно
те если несобственный интеграл сходится (расходится) то и ряд сходится (расходится)

если Iконечное число то ряд сходится ; если Iравно бесконечности ряд расходится
3. Знакопеременные и знакочередующиеся ряды. Абсолютная и условная сходимость. Достаточный признак сходимости знакопеременного ряда. Теорема Лейбница.
Ряд, среди членов которого встречаются как положительные, так и отрицательные, называется знакопеременным.
Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин.
Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин расходится, то знакопеременный ряд называется условно сходящимся.
Знакочередующимся рядом называется ряд вида а1 - а2 + а3 - а4 +...+ (-1)n+1an +... , все аn>0
Пусть знакочередующийся ряд удоволетворяет условию а1 >= a2 >= a3 >= ... >= an >=...> 0, т. е. lim an = 0. Тогда знакочередующийся ряд сходится, его сумма неотрицательна и не превосходит первый член.
Знакочередующийся ряд а1-а2+а3-а4+...+(-1)n+1an+... называется рядом Лейбница, если 1) а1 > a2 > a3 > a4>... > an >...
2) lim an = 0
Теорема Лейбница: ряд Лейбница сходится.
Следствие теоремы Лейбница: Если от ряда Лейбница отбросить первые n-членов, то оставшийся ряд будет рядом Лейбница. Частичная сумма ряда Лейбница отличается от суммы ряда Лейбница на величину, не превосходящую по модулю числа an+1
4. Функциональный ряд. Область сходимости. Равномерная сходимость. Степенной ряд. Теорема Абеля.
U1(x)+…+Un(x)+… (1)
Выражение вида (1) наз. Функциональным радом.
Определение: совокупность всех значений x при которых ряд сходится наз областью сходимости ряда.
Ряд (1) наз мажорируемым если существует сходящийся числовой ряд с положительными членами такой что │U1(x)│≤ a1
……………..
│Un(x)│≤ an
Определение: Если функциональный ряд (1) сходится ,т.е. он имеет сумму S(x), то го сумма зависит от x.
Теорема1: Сумма ряда непрерывных функций мажорируемых на некотором отрезке [a;b], есть функция непрерывная на этом отрезке
Теорема2: Если ряд (1) составленный из функций имеющие непрерывные производные на [a;b] сходится на этом отрезке к сумме S(x) и ряд составленный из производных мажорируем на этом отрезке,то сумма ряда производных = производной от суммы первоначального ряда.
СТЕПЕННОЙ РЯД
Функциональный ряд вида а0+а1(х-х0)+….+аn(x-x0) (2) наз степенным рядом.
Теорема Абеля: Если степенной ряд (2) сходится при некотором значении х1, то он абсолютно сходится при всех значениях х удовлетворяющий неравенству │x-x0│>│x1-x0│. Если степенной ряд (2) расходится то он расходится при всех значениях х удовлетворяющих неравенству │x-x0│>│x2-x0│
Док-во
Пусть степенной ряд сходится про х1 тогда: а0+а1(х1-х0)+…+аn(x1-x0)^n
Рассмотрим ряд составленный из модулей: │а0│+│а1(х1-х0)│+…+│аn(x-x0)^n│(x-x0)/x1-x0│+… (3) По признаку сравнения ряд сходится. Теорема доказана.
5. Ряды Тейлора и Маклорена. Биноминальный ряд. Разложение некоторых элементарных функций в ряд Маклорена.
5 ) Ряды Тейлора и Маклорена.
функция 
 раз дифференцируема в точке
раз дифференцируема в точке 


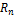 =0
=0
Пусть f(x) дифференцируема любое число раз в окрестности точки х0 тогда f(x)= 



Ряд 
Называется рядом Тейлора
Ряд Тейлора сходится и его сумма равна значению функции
В частном случае x0=0 тогда ряд называется Ряд Маклорена
Разложение Некоторых элементарных функций в ряд Маклорена
 ,
, 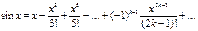


 ,
, 
Биномиальный ряд- ряд вида 
Б. р. сходится: при —1 < x <1, если n < —1; при —1< x  1, если —1 < n < 0; при —1< x
1, если —1 < n < 0; при —1< x  1, если n > 0.
1, если n > 0.
7. Комплексные числа и действия над ними. Геометрическая интерпретация комплексного числа модуль и аргумент комплексного числа. Тригонометрическая форма записи комплексного числа.
Теорема. При умножении двух комплексных чисел модуль произведения равен произведению модулей сомножителей, аргумент произведения равен сумме.
Док-во.
z1=x1+i*y1=|z1|*(cosφ1+i*sinφ1)
z2=x2+i*y2=|z2|*(cosφ2+i*sinφ2)
z=z1*z2=|z1|*|z2|*|cos φ1* cosφ2+i* sinφ1* cosφ2+ cosφ1* i*sinφ2+ i*sinφ1* i*sinφ2|=|z1|*|z2|*|cos(φ1+φ2)+i*sin(φ1+φ2)|=|z|*(cosφ+i*sinφ)
Следствие. Модуль частного двух комплексных чисел равен частному модулей. Аргумент частного равен разности соответствующих модулей.
Док-во.  =
=  =
= 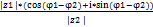
 =
= 
Замечание. Число  симетрично числу z относительно вещественной оси. arg
симетрично числу z относительно вещественной оси. arg  = - arg z.
= - arg z. 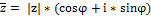 Следствие 2.
Следствие 2. 

 =
= 
 |z1|*
|z1|*  |z2|*
|z2|*  = |z1|*|z2|*
= |z1|*|z2|* 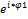 *
* 
 |z1|*|z2|*
|z1|*|z2|* 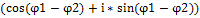 = |z1|*|z2|*
= |z1|*|z2|* 
|
из
5.00
|
Обсуждение в статье: Интегральный признак Коши |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

