 |
Главная |
Определение устойчивости систем автоматического регулирования по критерию Михайлова
|
из
5.00
|
Критерий позволяет судить об устойчивости САР по очертаниям так называемой кривой Михайлова, представляющей собой годограф вектора M(jw). Для этого необходимо определить характеристическое уравнение замкнутой системы и произвести замену s на jw.В результате замены получаем выражение:

Выделим вещественную и мнимую части вектора Михайлова в выражении:
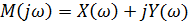
где


Изменяем частоту w от нуля до бесконечности и строим годограф на комплексной плоскости. Кривая Михайлова строится в плоскости (X, jY) по точкам в соответствии с выражением. Каждой точке кривой соответствует свое значение w. Направление возрастания w обычно указывается стрелкой на кривой.
Для устойчивости линейной САР необходимо и достаточно, чтобы вектор M(jw) при изменении w от нуля до бесконечности начинаясь на положительном направлении вещественной оси X повернулся на угол j=pn/2 против часовой стрелки, где n-степень характеристического уравнения замкнутой системы.
Таким образом, для практического применения критерия необходимо найти характеристический полином замкнутой системы M(s), построить по точкам кривую Михайлова M(jw) и подсчитать угол j на который поворачивается этот вектор. Если кривая Михайлова имеет плавные спиралеобразные очертания и проходит последовательно n - квадрантов, где n - порядок дифференциального уравнения САР, то такая система будет устойчивой.

| Рис. 1 Кривые Михайлова для устойчивых САР различного порядка |
Определение устойчивости систем автоматического регулирования по критерию Найквиста.
Критерий Найквиста позволяет вести анализ на устойчивость замкнутых систем САР в зависимости от устойчивости или неустойчивости разомкнутых систем регулирования. В соответствии с этими задачами критерий имеет следующую формулировку:
Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо достаточно, чтобы амплитудно-фазо-частотная характеристика (АФЧХ) разомкнутой системы не охватывала точку с координатами [-1, j0].
Для построения АФЧХ разомкнутой системы в передаточной функции производят замену s на j  , освобождаются от мнимости в знаменателе, умножая числитель и знаменатель на комплексно-сопряженное выражение, и выделяют действительную и мнимую части АФЧХ.
, освобождаются от мнимости в знаменателе, умножая числитель и знаменатель на комплексно-сопряженное выражение, и выделяют действительную и мнимую части АФЧХ.

После этого, задавая различные значения  в диапазоне от 0 до
в диапазоне от 0 до  , строят годограф W
, строят годограф W  .
.
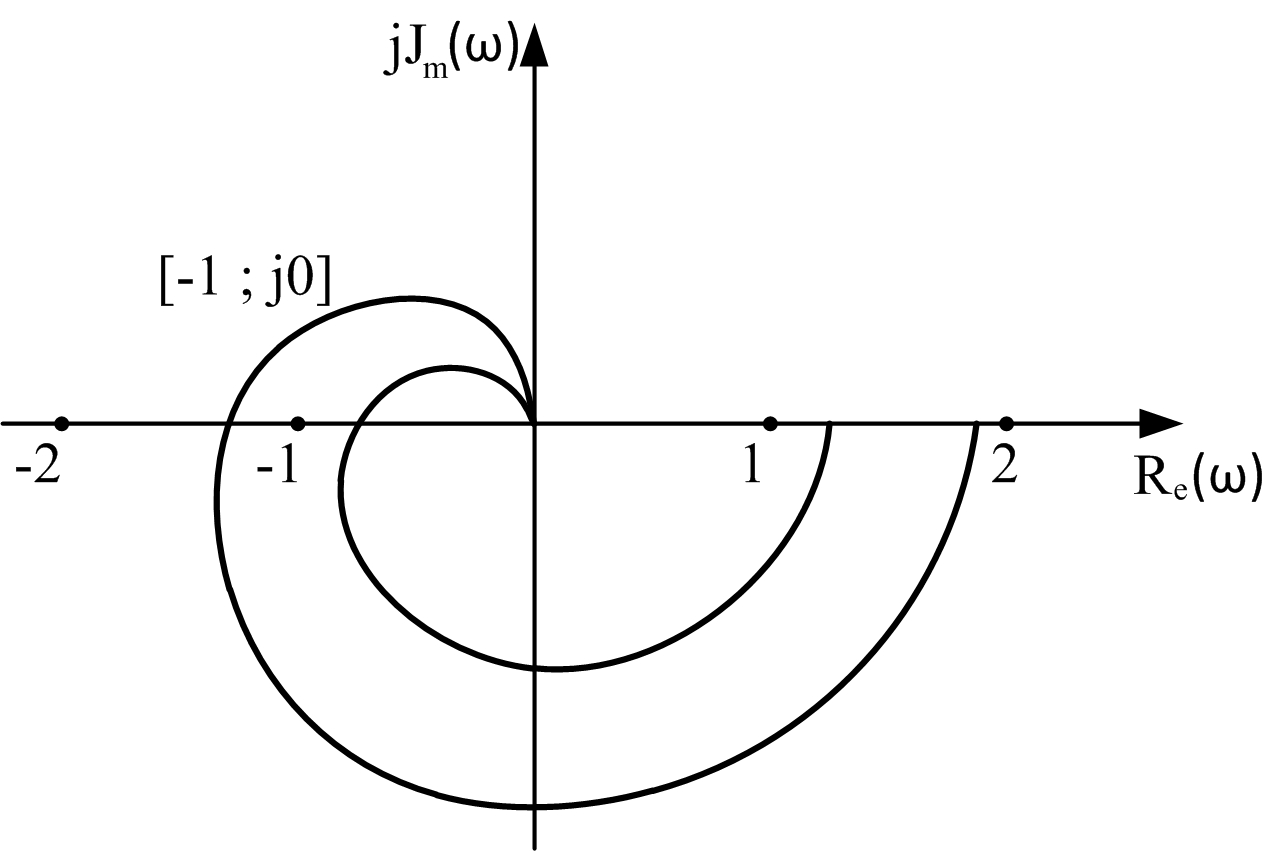
| Рис. 2 АФЧХ разомкнутой системы (1 -устойчивая САР, 2 – неустойчивая САР) |
АФЧХ может быть построена другим способом:
W(j  ) = A(
) = A( 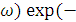 j
j 
где А - модуль АФЧХ;
 аргумент АФЧХ.
аргумент АФЧХ.
А(  j
j  =
= 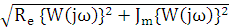 ;
;
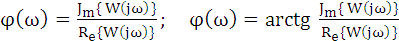 .
.
|
из
5.00
|
Обсуждение в статье: Определение устойчивости систем автоматического регулирования по критерию Михайлова |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

