 |
Главная |
Элементы вариационного исчисления
|
из
5.00
|
Пример 1 (задача о брахистохроне)
Исторически первой задачей о вариационном исчислении была задача о брахистохроне, поставленная И.Бернулли: среди всех кривых, соединяющих две данные точки плоскости, найти ту, двигаясь по которой под действием силы тяжести, материальная точка попадает из начальной точки в конечную за кротчайшее время (рис. 1). Кривая, вдоль которой тело, скорее всего скатывается из начальной точки в конечную, называется брахистохроной.
 Рис. 1.
Рис. 1.
Построим математическую модель задачи. Введем систему координат, начало которой совместим с точкой  . Представим искомую кривую уравнением
. Представим искомую кривую уравнением  ,
, 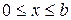 . Применим закон сохранения энергии, трением и сопротивлением среды пренебрегаем
. Применим закон сохранения энергии, трением и сопротивлением среды пренебрегаем
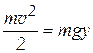 ,
,
где  – масса тела,
– масса тела,  – ускорение свободного падения,
– ускорение свободного падения,  – величина скорости.
– величина скорости.
Если  , где,
, где, 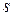 – путь, пройденный телом, то
– путь, пройденный телом, то 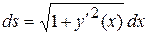 ,
, 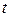 – время движения.
– время движения.
Тогда
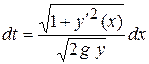 .
.
Полное время движения из точки 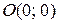 в точку
в точку  выражается интегралом
выражается интегралом
 .
.
Искомая кривая 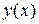 должна удовлетворять условию
должна удовлетворять условию

и условиям
 ,
,  .
.
Определение. Переменная величина 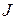 называется функционалом, зависящим от функций
называется функционалом, зависящим от функций 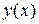 , принадлежащих некоторому классу функций
, принадлежащих некоторому классу функций  , если каждой функции
, если каждой функции  , согласно некоторому правилу, соответствует единственное число, которое записывается
, согласно некоторому правилу, соответствует единственное число, которое записывается
 .
.
Таким образом, функционал – это отображение
 .
.
Класс функций  , на котором определен функционал называется областью определения функционала и обозначается
, на котором определен функционал называется областью определения функционала и обозначается  , а множество
, а множество 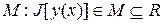 называется множеством значений функционала
называется множеством значений функционала 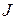 .
.
Пример 2 (цепная линия)
Найдём форму, какую принимает тонкая гибкая однородная нить (цепь) длины  под действием силы тяжести.
под действием силы тяжести.

Рис. 2.
Пусть система  выбрана так, что ось
выбрана так, что ось  горизонтальна, ось
горизонтальна, ось  направлена вертикально вверх, а координаты точек подвеса суть
направлена вертикально вверх, а координаты точек подвеса суть  и
и  (рис.2). Пусть далее,
(рис.2). Пусть далее, 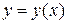 задаёт линию, занимаемую цепью. Из механики известно, что получающаяся форма цепи
задаёт линию, занимаемую цепью. Из механики известно, что получающаяся форма цепи 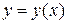 соответствует экстремуму её потенциальной энергии
соответствует экстремуму её потенциальной энергии
 ,
,
где  – плотность материала цепи,
– плотность материала цепи,  – ускорение свободного падения.
– ускорение свободного падения.
Искомая форма цепи 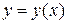 должна удовлетворять условию
должна удовлетворять условию
 ,
,
краевым условиям
 ,
,  ,
,
и условию, определяющему длины цепи
 .
.
Приведенные примеры относятся к задаче на минимум функционала вида
 ,
,
который часто встречается в практических приложениях.
Вариационное исчисление занимается условиями существования экстремума и методами их нахождения.
Обозначим через 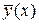 некоторую фиксированную функцию из области определения функционала
некоторую фиксированную функцию из области определения функционала  .
.
Разность
 ,
,
называют вариацией аргумента функционала 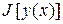 .
.
Вариация функции  является функцией
является функцией 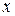 . Эту функцию можно дифференцировать несколько раз, причем, нетрудно видеть что
. Эту функцию можно дифференцировать несколько раз, причем, нетрудно видеть что
 .
.
Приращением функционала, отвечающим приращению аргумента 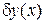 , называется величина
, называется величина
 ,
,
где 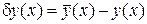 ,
,  ,
,  .
.
Если  может быть представлено в виде
может быть представлено в виде
 ,
,
где 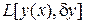 – линейный (и, стало быть, ограниченный) функционал относительно
– линейный (и, стало быть, ограниченный) функционал относительно 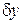 , а функционал
, а функционал  при норме
при норме  , то L называют вариацией функционала
, то L называют вариацией функционала  и обозначают
и обозначают
 .
.
Для  нормой можно взять
нормой можно взять
 .
.
Формально, существование вариации функционала связывают с условием его дифференцируемости
 .
.
Пример. Найдем вариацию функционала 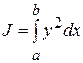 .
.
Имеем 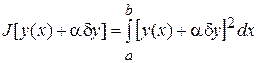 .
.
Тогда  ,
,
и, следовательно  .
.
Для функционала

найдем первую вариацию.

 ,
,
или
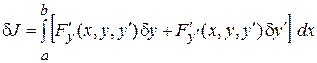 .
.
Теорема. Если функционал  , определенный на
, определенный на  имеющий вариацию, достигает экстремума на функции
имеющий вариацию, достигает экстремума на функции  , то
, то
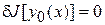 .
.
Рассмотрим функционал
 ,
,
с заданными граничными условиями:  ,
,  .
.
Предположим, данный функционал достигает экстремум в точке  . Тогда, согласно необходимому условию существования экстремума
. Тогда, согласно необходимому условию существования экстремума
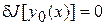 .
.
В найденной вариации  проинтегрируем второе слагаемое по частям:
проинтегрируем второе слагаемое по частям:
 .
.
С учетом условий  и
и  , имеем
, имеем  , и получаем
, и получаем
 .
.
Согласно необходимому условию существования экстремума
 .
.
В этом выражении вариация 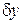 является произвольной непрерывной функцией на
является произвольной непрерывной функцией на  , так что получаем
, так что получаем
 .
.
Полученное дифференциальное уравнение называется уравнением Эйлера для функционала  .
.
Таким образом, условие существования экстремума функционала  при условиях
при условиях  ,
,  приводит к краевой задаче для дифференциального уравнения
приводит к краевой задаче для дифференциального уравнения  при тех же условиях
при тех же условиях  ,
,  .
.
Любое решение задачи
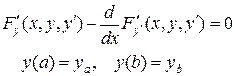 ,
,
называется экстремалью.
Если в уравнении  раскрыть производную, то получим краевую задачу
раскрыть производную, то получим краевую задачу
 .
.
 .
.
|
из
5.00
|
Обсуждение в статье: Элементы вариационного исчисления |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

