Задачи для самостоятельного решения. 1). Найти все значения параметра а, при которых корни уравнения принадлежат отрезку

 

1). Найти все значения параметра а, при которых корни уравнения 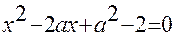принадлежат отрезку .

 

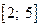Ответ: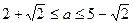

2). При каких значениях а только больший корень принадлежит

промежутку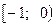

 

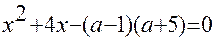
Ответ:

3).При каких а оба корня уравнения х2 –6ах +2-2а+9а2=0 больше 3?

 

4).При каких а оба корня уравнения х2 –ах=2=0 лежат на интервале (0;3)?

5). При каких а один корень уравнения ах2 +х+1=0 больше 2, а другой меньше 2?

Решение биквадратных уравнений

Пример 1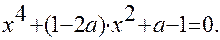

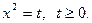
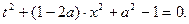
- меньший корень

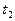- больший корень

Схема решения уравнения

 

1). Уравнение не имеет решение
2). Уравнение имеет одно решение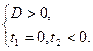
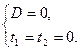
3). Уравнение имеет два решения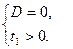
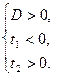
4). Уравнение имеет три решения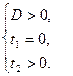
5). Уравнение имеет четыре решения

 

 

Задача 1. При каких значениях параметра а уравнение

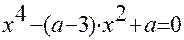
не имеет корней ?

Решение: Уравнение 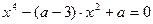является биквадратным. Сделав замену 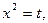где получим новое уравнение

,

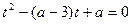оказавшиеся квадратным.

Для того чтобы исходное уравнение не имело корней, новое уравнение либо вообще не должно иметь корней, либо оба его корня (равные или различные ) должны быть отрицательными.

Найдем дискриминант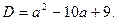

Квадратное уравнение не имеет корней, если его дискриминант то есть 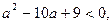откуда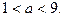

Оба корня будут отрицательными, если 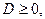Отрицательно, а произведение положительно, а тогда имеем систему

 

 

 

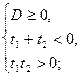
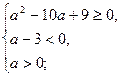
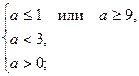
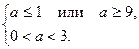
Решением последней системы является промежуток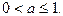

Объединив промежутк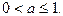и и 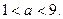получим промежуток, 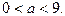Итак , исходное уравнение не имеет корней при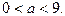

 

Ответ: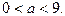

 

Задача2. В зависимости от значений параметра а определить количество корней уравнения

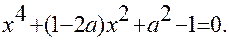(1)

Решение:

Полагая 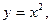перепишем уравнение (1) в виде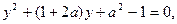

 

Откуда находим

 

Таким образом, уравнение (1) будет иметь четыре корня, если значение параметра а удовлетворяют системе неравенств

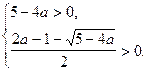
Решая последнюю систему, получаем, что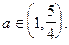

Очевидно также, что уравнение (1) имеет три корня, если значения параметра а удовлетворяют системе

Далее уравнение (1) имеет два корня, если значения параметра а удовлетворяют ими систем неравенств

 

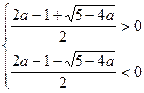
Или система

 

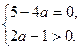
В первом случае 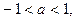втором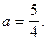

Теперь, если значение параметра а удовлетворяют системе

Т.е. если 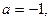то уравнение (1) имеет одно решение.

Наконец, уравнение (1) не будет иметь решений при тех значениях параметра а, которые удовлетворяют совокупности

 

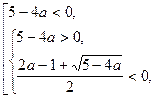
Ответ: если 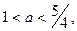то четыре корня;

если 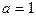то три корня;

если то два корня;

если 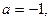то один корень;

если 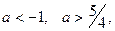то нет корней.

 

 

Задачи для самостоятельного решения

 

1). Найти все значения параметра а, при которых уравнение

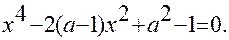
а) не имеет корней

б) имеет только один корень

в) имеет два различных корня

г) имеет четыре различных корня

 

Ответ:

а)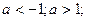

б)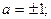

в)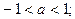

г)

 

.