Основные математические функции

Функция	Тип аргумента	Тип результата	Математическое значение
ABS(x)	I R	I R	|x| (абсолютная величина)
MOD(x,y)	I	I	Остаток от деления x на y
SQRT(x)	R C	R C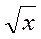
EXP(x)	R C	R C	ex
LOG(x)	R C	R C	Ln x
LOG10(x)	R C	R C	Lg x
SIN(x)	R C	R C	Sin x (x в радианах)
SIND(x)	R C	R C	Sin x (x в градусах)
COS(x)	R C	R C	cos x (x в радианах)
COSD(x)	R C	R C	cos x (x в градусах)
TAN(x)	R C	R C	tg x (x в радианах)
TAND(x)	R C	R C	tg x (x в градусах)
COTAN(x)	R C	R C	ctg x (x в радианах)
ASIN(x)	R	R	arcsin x (радианы)
ASIND(x)	R	R	arcsin x (градусы)
ACOS(x)	R	R	arccos x (радианы)
ACOSD(x)	R	R	arccos x (градусы)
ATAN(x)	R	R	arctg x (радианы)
ATAND(x)	R	R	arctg x (градусы)

В некоторых функциях из следующего списка происходит преобразование типа (тип аргумента и результата разные):

NINT(r) — ближайшее целое к значению вещественного аргумента,

ANINT(r) — вещественная форма ближайшего целого,

AINT(r) — вещественная форма целой части,

CEILING(r) — ближайшее целое, большее r

FLOOR(r) — наибольшее целое, не превосходящее аргумента,

REAL(c) — вещественная часть комплексного аргумента,

AIMAG(c) — мнимая часть комплексного аргумента,

CMPLX(x[,y]) — комплексное число с указанными частями.

Перечисляемые ниже функции сохраняют тип своего аргумента:

CONJG(z) — сопряженное значение комплексной переменной z,

MAX(a1, а2 [, а3,...]) — максимальное из значений аргумента (аналогично MIN — минимальное),

MODULO(a,m) = a-floor(a/m)*m (а и m целые либо вещественные),

SIGN(a,b) — модуль а со знаком b.

Отметим, что перечисленные имена являются родовыми и фактически определяют семейство функций, каждое из которых выполняет нужные вычисления для аргументов различных встроенных типов и возвращает результат того же типа. Чаще всего можно ограничиться этим родовым именем, однако при вызове процедур с аргументом-функцией необходимо подставлять специфическое имя последней (см. более подробные руководства).

К встроенным процедурам можно обращаться с ключевыми фактическими параметрами. Например,

CALL date_and_time (time=t)

присваивает текущее время текстовой переменной t в формате ччммсс.ссс, где ч, м и с означают цифры часов, минут и секунд соответственно. Другие необязательные параметры в данном обращении отсутствуют.

Оператор присваивания, инициализация и изменение значений пере­менных.Формат оператора присваивания:

переменная = выражение

Оператор присваивания задает переменной, указанной в его левой части, значение правой. Правая часть в общем случае определяется выражением, которое предварительно вычисляется. Выражение в левой части стоять не может.

Приведем примеры операторов присваивания:

y = a*x**2+b*x+c

n = n+1

Второй пример (читается: "n присвоить n +1") наглядно демонстрируетразличие между равенством и присваиванием и динамический смысл последнего: в правой части используется старое, а в левой – новое значение переменной.

Левая и правая части оператора присваивания должны быть согласованы по типу: обе быть числового, логического, символьного или общего производного типа. Предполагается, что все переменные, входящие в правую часть, были предварительно означены (нарушение этого требования компилятором не обнаруживается).

При выполнении "численного" присваивания тип результата преобразуется к типу левой части, причем допускается как сужение типа (например, присваивание целой переменной вещественного значения), так и его обобщение. При сужении происходит частичная потеря информации – в частности, округление значения правой части.

Никакой автоматической инициализации переменных (например, обнуления) Фортран не производит. Начальные значения переменных могут быть присвоены обычными операторами присваивания, а также заданы непосредственно при их описании, например

real:: х=1.7, у=6.94

Для инициализации большого числа переменных предпочтительно применение оператора

dataх/1.7/, у/6.94/ или data х,у /1.7, 6.94/.

Простейший ввод-вывод.Простейший ввод данных в программу организуется с клавиатуры оператором вида

read *,список ввода

Например:

read *,х,у

При выполнении оператора значения вводимых переменных вводятся в одну строку через пробел или запятую. Оператор read * с пустым списком ввода можно применять для организации паузы в вычислениях (например, внутри циклов).

Вывод на экран можно осуществлять оператором

print *, список вывода,

где список вывода может включать константы, переменные, выражения. Например:

print *, 'Сумма ряда=', S

позволит вывести результат с поясняющим его текстом (например, "сумма ряда = "). Значение результата будет выведено в формате, определяемом описанием соответствующей переменной. Более сложные конструкции, позволяющие управлять формой вывода и обменом информацией с файлами, обсуждаются позднее.

Упражнения

1. Для следующих формул записать соответствующие арифметические выражения на Фортране:

а) a + bx + cyz;	б) [(ax – b)x + c]x – d;
в)	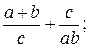г)
д)	е)

2. Записать математические формулы, соответствующие следующим выражениям на Фортране:

а) (p + q) / (r + s) – p * q / (r * s);

б) 1E3+beta / (x – gamma * delta);

в) a / b * (c + d) – (a – b) / b / c + 1E–8.

3. Почему на Фортране аргумент функции всегда записывают в скобках (например, пишут log(5), а не log5)?

4. Для следующих формул записать соответствующие арифметические выражения на Фортране:

a) (1 + x)2;	б)	в)	г)
д) arcsin x;	е)	ж)	з)
и)	к)	л)

5. Определить результаты вычисления выражений

1) 3/2/5 2) 3./2/5 3)3/2/5. 4) 3/2./5.

6. Определить тип выражения:

7. Записать арифметическое выражение, вычисляющее

а) сумму цифр целого двузначного числа X

b) сумму цифр целого четырехзначного числа Х

8.Записать последовательность операторов присваивания, осуществляющих

1) обмен значений в двух переменных

2) циклический обмен значений в трех переменных

3) обмен значений двух целых переменных без использования третьей переменной; обосновать ограниченность такого метода.

9. Написать программу на Фортране вычисления площади кольца по значениям внешнего и внутреннего радиусов.