 |
Главная |
Лабораторная работа №10
|
из
5.00
|
Цель:применениеметодов математической физики (уравнение колебания струны, уравнение теплопроводности).
Задача 1. Исследовать процесс колебания жестко закрепленной струны. Выделить мажоранту и миноранту полученного ряда.
Решение. Уравнение колебания струны.
Рассматривается уравнение колебания жестко закреплённой струны 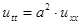 в области
в области 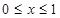 ,
,  , (1.1)
, (1.1)
при граничных условиях 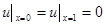 , (1.2)
, (1.2)
и начальных условиях 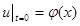 ,
,  . (1.3)
. (1.3)
Здесь  – постоянная скорость распространения звука в среде,
– постоянная скорость распространения звука в среде, 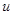 – отклонение струны от положения равновесия в точке
– отклонение струны от положения равновесия в точке 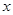 в момент времени
в момент времени 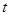 ,
, 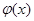 и
и 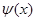 – заданные начальное отклонение и начальная скорость отклонения струны. Для решения рекомендуется применять метод разделения переменных
– заданные начальное отклонение и начальная скорость отклонения струны. Для решения рекомендуется применять метод разделения переменных
Метод разделения переменных. Точное решение исходной задачи.
Для получения точного решения исходной задачи (1.1)-(1.3) применим метод разделения переменных Фурье. Будем искать решение в виде:
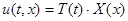 .
.
Подставляя в уравнение (1.1), получим
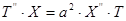 .
.
Разделим это равенство на 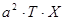 .
.
Тогда 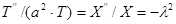 . (1.4)
. (1.4)
Следует отметить, что функция, стоящая в левой части равенства зависит от 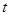 , а в правой – от
, а в правой – от 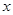 . Следовательно, эти величины есть константа. Обозначим эту константу
. Следовательно, эти величины есть константа. Обозначим эту константу 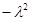 .
.
Рассмотрим правую часть равенства (1.4).
Уравнение 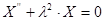 при условиях
при условиях 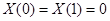 , имеет решение
, имеет решение 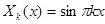 ,
, 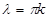 ,
, 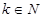 .
.
Тогда из левой части (1.4) следует, что 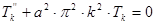 и
и
 .
.
Используя линейность исходной задачи (линейная комбинация решений есть решение) отсюда получаем:
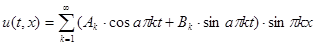 . (1.5)
. (1.5)
Подставляя начальные условия (1.3), находим уравнения для определения 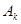 и
и  :
:
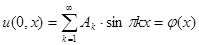 ,
,
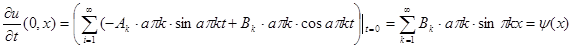
Тем самым показано, что искомые 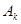 и
и  выражаются через коэффициенты Фурье разложений функций
выражаются через коэффициенты Фурье разложений функций 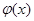 и
и 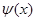 по синусам (т.е. функции
по синусам (т.е. функции 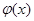 ) и
) и 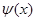 продолжаются нечетным образом на отрезок
продолжаются нечетным образом на отрезок 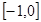 и получающиеся функции продолжаются периодическим образом с периодом 2).
и получающиеся функции продолжаются периодическим образом с периодом 2).
Искомые 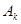 и
и  определяются по следующим формулам:
определяются по следующим формулам:
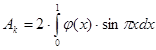 ,
,
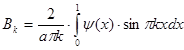 . (1.6)
. (1.6)
Итак, ряд (1.5), где 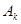 и
и  определены (1.6), представляет точное решение задачи (1.1)-(1.3). Скорость сходимости этого ряда, а, следовательно, и применимость указанных формул для численных расчетов решения определяется гладкостью начальных функций
определены (1.6), представляет точное решение задачи (1.1)-(1.3). Скорость сходимости этого ряда, а, следовательно, и применимость указанных формул для численных расчетов решения определяется гладкостью начальных функций 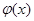 и
и 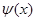 .
.
Задача 2.Исследовать изменение температуры в точке 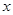 в момент времени
в момент времени 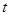 в рамках уравнения теплопроводности. Выделить мажоранту и миноранту полученного ряда.
в рамках уравнения теплопроводности. Выделить мажоранту и миноранту полученного ряда.
Решение: Уравнение теплопроводности.
Рассмотрим уравнение теплопроводности
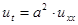 в области
в области 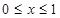 ,
,  , (2.1)
, (2.1)
при граничных условиях 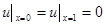 , (2.2)
, (2.2)
и начальных условиях 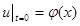 (2.3)
(2.3)
Здесь  – постоянный коэффициент теплопроводности,
– постоянный коэффициент теплопроводности, 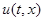 – искомая температура в точке
– искомая температура в точке 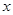 в момент времени
в момент времени 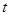 ,
, 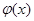 – заданная температура в начальный момент времени.
– заданная температура в начальный момент времени.
Разбор одного варианта. Рассмотрим решение уравнения колебания струны
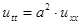 в области
в области 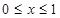 ,
,  , (2.4)
, (2.4)
при граничных условиях 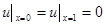 , (2.5)
, (2.5)
и начальных условиях 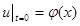 ,
, 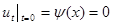 , (2.6)
, (2.6)
где 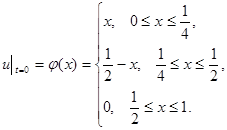 . (2.7)
. (2.7)
Решения рекомендуется получить в виде ряда Фурье.
|
из
5.00
|
Обсуждение в статье: Лабораторная работа №10 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

