 |
Главная |
Методические указания к выполнению контрольной работы по курсу «Цифровые многомерные системы управления»,
|
из
5.00
|
ИДЕНТИФИКАЦИЯ ДИСКРЕТНОЙ ДИНАМИЧЕСКОЙ МОДЕЛИ ПО ИМИТАЦИОННОЙ МОДЕЛИ ОБЪЕКТА
Методические указания к выполнению контрольной работы по курсу «Цифровые многомерные системы управления»,
«Цифровые системы управления технологическими
Процессами»
Цель работы: изучение методов построения дискретных динамических моделей, используемых при синтезе цифрового управления, и идентификация параметров моделей объектов регулирования, описываемых конечно-разностными уравнениями.
1. МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ РАБОТЫ
1.1 Построение математических моделей объектов
регулирования с помощью конечно-разностных уравнений и
дискретных передаточных функций
Методы расчета и синтеза цифровых систем управления существенно отличаются от классических методов, применяемых для непрерывных систем. Это связано с тем, что основой математического аппарата построения цифровых систем являются разностные схемы, которые заменяют дифференциальные уравнения, описывающие непрерывные системы. Цифровые системы отличаются от аналоговых тем, что сигнал в одной или нескольких точках представляет собой цифровой код. Поэтому алгоритмы, применяемые при расчете цифровых систем, могут быть реализованы только с помощью ЭВМ.
В реальных системах управления могут присутствовать как аналоговые, так и цифровые сигналы. Поэтому такие системы в целом называет дискретными. Преобразование аналоговых сигналов в цифровые и обратно осуществляется с помощь аналого-цифровых и цифро-аналоговых преобразователей.
Непрерывная модель, описывающая поведение объекта с сосредоточенными параметрами, представляет собой непрерывную функцию 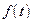 и может быть интерпретирована в виде графика (рис.1).
и может быть интерпретирована в виде графика (рис.1).

Рис.1. График функции 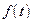
Весь диапазон времени разбивается на равные интервалы. 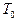 - такт квантования. Обозначим
- такт квантования. Обозначим 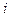 - текущий индекс (номер) такта квантования.
- текущий индекс (номер) такта квантования.
При малых тактах квантования разностные уравнения можно получать из дифференциальных путем дискретизации последних [2]. В частности, дифференциалы могут приближенно заменяться правыми разностями:
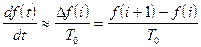 ;
;
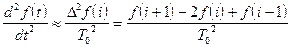 ; (1)
; (1)
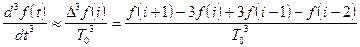 .
.
Таким образом можно получить производную  - го порядка в виде разностной схемы.
- го порядка в виде разностной схемы.
Из теории автоматического управления известно, что модели (рис.2) динамических объектов с запаздыванием в непрерывном виде могут быть представлены дифференциальными уравнениями или соответствующими передаточными функциями:
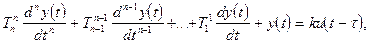 (2)
(2)
или
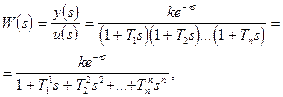 (3)
(3)
где 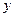 - выходной сигнал объекта;
- выходной сигнал объекта; 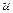 - входной сигнал объекта;
- входной сигнал объекта; 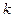 - коэффициент усиления объекта;
- коэффициент усиления объекта; 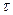 - время чистого запаздывания объекта;
- время чистого запаздывания объекта; 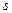 - оператор преобразования Лапласа;
- оператор преобразования Лапласа; 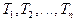 - постоянные времени объекта, по которым могут вычисляться коэффициенты
- постоянные времени объекта, по которым могут вычисляться коэффициенты  дифференциального уравнения (2):
дифференциального уравнения (2):
при 
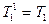 ,
,
при 
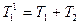 ,
, 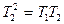 ,
,
при 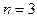
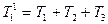 ,
, 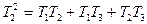 ,
,
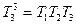 .
.

Рис.2. Динамическое звено с одним входом и выходом
Если система регулирования реализуется на ЭВМ, то необходимо дискретное (цифровое) представление динамических моделей. В этом случае согласно выражениям (1) непрерывному дифференциальному уравнению (2) соответствует конечно-разностное уравнение
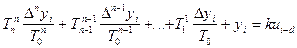 , (4)
, (4)
а непрерывной передаточной функции (3) соответствует дискретная передаточная функция [5]:
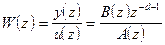 , (5)
, (5)
где 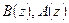 - полиномы числителя и знаменателя дискретной передаточной функции;
- полиномы числителя и знаменателя дискретной передаточной функции;  - оператор сдвига;
- оператор сдвига;  - целое число тактов запаздывания, соответствующее времени чистого запаздывания
- целое число тактов запаздывания, соответствующее времени чистого запаздывания 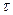 .
.
Если  при вычислении не является целым числом, то оно округляется до ближайшего целого.
при вычислении не является целым числом, то оно округляется до ближайшего целого.
Например, апериодическое звено второго порядка с чистым запаздыванием представляется в виде дифференциального уравнения второго порядка
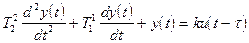 , (6)
, (6)
или соответствующей передаточной функции
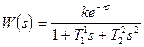 . (7)
. (7)
Из дифференциального уравнения (6) получим конечно-разностное:
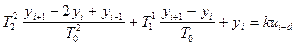 . (8)
. (8)
Преобразуя это уравнение, выразим из него 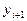 .
.
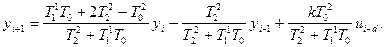 (9)
(9)
Введем обозначения:
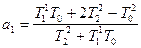 , (10)
, (10)
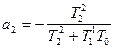 , (11)
, (11)
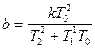 . (12)
. (12)
Отсюда
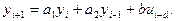 (13)
(13)
Уменьшая текущий индекс такта квантования на единицу в левой и правой частях уравнения (13), получим конечно-разностное уравнение второго порядка, удобное для практического использования:
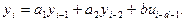 (14)
(14)
Для систем, описываемых линейными конечно-разностными уравнениями с постоянными коэффициентами, используется операционное исчисление, в котором входные и выходные величины описываются оператором сдвига 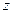 аналогично оператору Лапласа
аналогично оператору Лапласа 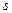 :
:
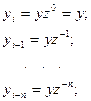
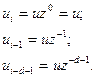 (15)
(15)
Использование оператора сдвига  позволяет получить из конечно-разностного уравнения передаточную функцию в
позволяет получить из конечно-разностного уравнения передаточную функцию в 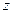 - преобразовании. Используя соотношения (15) для уравнения второго порядка (14) получим
- преобразовании. Используя соотношения (15) для уравнения второго порядка (14) получим
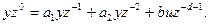 (16)
(16)
Отсюда дискретная передаточная функция
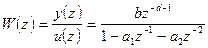 . (17)
. (17)
Это упрощает математические преобразования для получения разностных уравнений замкнутых цифровых систем регулирования. Аналогично можно получить конечно-разностные уравнения и передаточные функции в 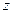 - преобразовании объектов и регуляторов, описываемых интегро-дифференциальными уравнениями любого порядка, в том числе типовых динамических звеньев и регуляторов.
- преобразовании объектов и регуляторов, описываемых интегро-дифференциальными уравнениями любого порядка, в том числе типовых динамических звеньев и регуляторов.
1.2 Имитационная модель объекта регулирования
При отсутствии реального объекта регулирования или невозможности получения его динамической характеристики (например, кривой разгона объекта) применяют имитационные модели.
Под имитационной моделью объекта регулирования понимается такая модель, которая имитирует поведение исследуемого объекта в реальных условиях. Имитационная модель не используется непосредственно для синтеза системы регулирования, а служит лишь источником информации о характере зависимости между входными и выходными параметрами объекта. Основным отличием реального объекта от его математической модели является наличие помех при измерении выходного сигнала 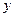 . Пренебрегая структурным несоответствием объекта и имитационной модели, примем в качестве объекта регулирования имитационную модель в виде конечно-разностного уравнения второго порядка с чистым запаздыванием с наложением случайной помехи
. Пренебрегая структурным несоответствием объекта и имитационной модели, примем в качестве объекта регулирования имитационную модель в виде конечно-разностного уравнения второго порядка с чистым запаздыванием с наложением случайной помехи 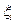 на выходную переменную:
на выходную переменную:
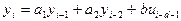 , (18)
, (18)
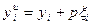 , (19)
, (19)
где 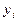 - выход объекта без помехи;
- выход объекта без помехи; 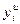 - измеряемое значение выходного сигнала с помехой
- измеряемое значение выходного сигнала с помехой 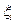 ;
; 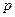 - коэффициент помехи, определяющий уровень помехи на каждом такте
- коэффициент помехи, определяющий уровень помехи на каждом такте 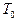 квантования;
квантования; 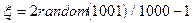 .
.
Расчет значения случайной помехи 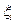 реализуется стандартным оператором – функцией
реализуется стандартным оператором – функцией 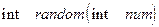 в языке
в языке 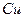 (генератор случайных чисел). Помеха
(генератор случайных чисел). Помеха 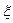 принимает значения в пределах от -1 до +1 случайным образом.
принимает значения в пределах от -1 до +1 случайным образом.
С помощью имитационной модели (18),(19) рассчитываются значения точек переходного процесса объекта регулирования с тактом квантования 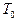 при различных значениях входного воздействия. Для расчета кривой разгона по имитационной модели необходимо знать параметры
при различных значениях входного воздействия. Для расчета кривой разгона по имитационной модели необходимо знать параметры 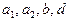 уравнения (18), такт квантования
уравнения (18), такт квантования 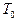 , коэффициент помехи
, коэффициент помехи 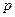 и задаться начальными условиями по входу и выходу объекта, а также величиной входного ступенчатого воздействия
и задаться начальными условиями по входу и выходу объекта, а также величиной входного ступенчатого воздействия 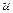 .
.
Для уравнения (18) начальные условия принимаются нулевыми и определяются его порядком:
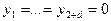 , (20)
, (20)
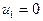 .
.
Если на вход имитационной модели подается единичное ступенчатое воздействие, то, начиная с такта квантования 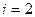 ,
, 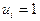
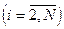 .
. 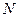 определяется временем переходного процесса
определяется временем переходного процесса  :
:
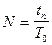 . (21)
. (21)
Так как  заранее не известно, то число
заранее не известно, то число 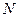 выбирается экспериментально подбором при расчете переходного процесса.
выбирается экспериментально подбором при расчете переходного процесса.
Вначале по уравнению (18) рассчитывается переходный процесс без помехи, начиная с такта  :
:
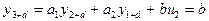 ;
;
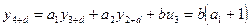 ; (22)
; (22)
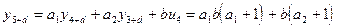 ;
;
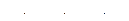
 ;
;
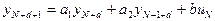 .
.
Затем по уравнению (19) рассчитывается переходный процесс объекта регулирования 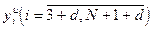 с учетом помехи
с учетом помехи 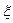 .
.
1.3 Параметрическая идентификация модели в условиях активного эксперимента
При синтезе оптимальной системы регулирования ставится две основные задачи:
1. Идентификация модели объекта регулирования.
2. Выбор структуры регулятора и оптимизация его настроек.
Рассмотрим подробно решение первой задачи.
Параметрическая идентификация заключается в расчете параметров 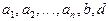 конечно-разностного уравнения модели объекта для выбранной структуры (порядка уравнения), обеспечивающих минимум отклонения переходного процесса, рассчитанного по полученной модели и кривой разгона объекта.
конечно-разностного уравнения модели объекта для выбранной структуры (порядка уравнения), обеспечивающих минимум отклонения переходного процесса, рассчитанного по полученной модели и кривой разгона объекта.
В качестве объекта регулирования примем имитационную модель (18),(19). На вход имитационной модели объекта подается единичное ступенчатое воздействие 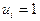
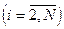 , т.е. проводится активный эксперимент. Точки кривой разгона
, т.е. проводится активный эксперимент. Точки кривой разгона 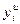 для заданного такта квантования
для заданного такта квантования 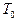 рассчитываются по уравнениям (18),(19). Ставится задача: по полученной на имитационной модели объекта регулирования кривой разгона найти параметры математической модели той же структуры, то есть восстановить коэффициенты
рассчитываются по уравнениям (18),(19). Ставится задача: по полученной на имитационной модели объекта регулирования кривой разгона найти параметры математической модели той же структуры, то есть восстановить коэффициенты 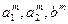 в уравнении (23):
в уравнении (23):
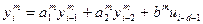 , (23)
, (23)
где 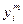 - выход восстанавливаемой модели объекта;
- выход восстанавливаемой модели объекта; 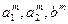 - восстанавливаемые коэффициенты модели объекта.
- восстанавливаемые коэффициенты модели объекта.
Поставленную задачу можно представить следующей структурной схемой (рис.3).
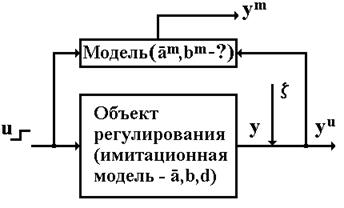
Рис.3. Структурная схема задачи идентификации в условиях активного эксперимента
Для решения поставленной задачи воспользуемся методом наименьших квадратов (МНК), широко применяющимся для параметрической идентификации моделей объектов регулирования. Критерием МНК является наилучшее совпадение переходных процессов 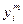 и
и 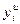 , определяемое выражением:
, определяемое выражением:
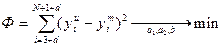 . (24)
. (24)
В уравнении (23) индекс 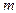 при
при 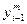 и
и  можно заменить на индекс
можно заменить на индекс 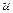 , т.к. для определения
, т.к. для определения 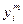 всегда известны измеренные значения
всегда известны измеренные значения 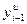 и
и  . Поэтому для любого
. Поэтому для любого 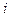 -го такта квантования справедливо:
-го такта квантования справедливо:
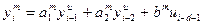 . (25)
. (25)
Подставив (25) в (24), получим:
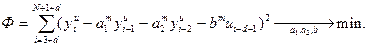 (26)
(26)
Так как функция  положительно определенная в силу квадратичной формы, то необходимым и достаточным условием экстремума
положительно определенная в силу квадратичной формы, то необходимым и достаточным условием экстремума  является равенство нулю первых производных по искомым параметрам:
является равенство нулю первых производных по искомым параметрам:
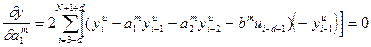 ;
;
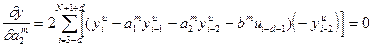 ; (27)
; (27)
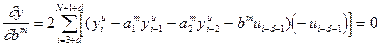 ;
;
После преобразования получим:
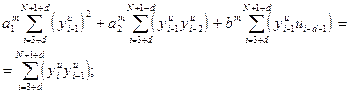
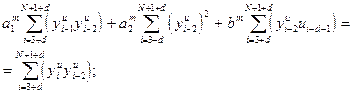 (28)
(28)
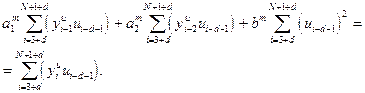
Параметры 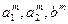 , удовлетворяющие критерию (24), находятся решением системы (28) линейных уравнений [1]. МНК в приведенной постановке со стохастическим возмущающим сигналом позволяет получить достоверные и несмещенные оценки параметров
, удовлетворяющие критерию (24), находятся решением системы (28) линейных уравнений [1]. МНК в приведенной постановке со стохастическим возмущающим сигналом позволяет получить достоверные и несмещенные оценки параметров 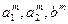 .
.
При равенстве нулю коэффициента помехи 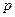 , т.е. при отсутствии возмущений на выходе имитационной модели, когда
, т.е. при отсутствии возмущений на выходе имитационной модели, когда  , оценки
, оценки 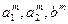 должны совпадать с
должны совпадать с 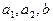 (до погрешности вычислений).
(до погрешности вычислений).
По полученным 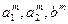 из системы (28) можно восстановить значения параметров соответствующей передаточной функции объекта (7)
из системы (28) можно восстановить значения параметров соответствующей передаточной функции объекта (7) 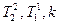 .
.
1.4 Установление адекватности полученной дискретной
модели объекту
После получения параметров 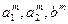 разностного уравнения (23) необходимо оценить меру соответствия полученной модели реальному объекту (имитационной модели), т.е. проверить адекватность модели объекту.
разностного уравнения (23) необходимо оценить меру соответствия полученной модели реальному объекту (имитационной модели), т.е. проверить адекватность модели объекту.
Адекватность устанавливается по критерию Фишера [3], для чего рассчитывается дисперсионное соотношение  :
:
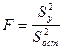 , (29)
, (29)
где 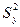 - дисперсия относительно среднего, характеризующая отклонение выхода объекта
- дисперсия относительно среднего, характеризующая отклонение выхода объекта 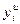 от среднего значения
от среднего значения 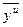 ;
; 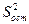 - остаточная дисперсия, характеризующая отклонение выхода модели
- остаточная дисперсия, характеризующая отклонение выхода модели 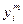 от выхода объекта
от выхода объекта 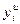 .
.
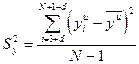 , (30)
, (30)
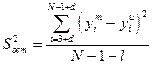 , (31)
, (31)
где 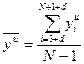 - среднее значение выхода объекта;
- среднее значение выхода объекта; 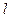 - число связей, наложенных на выборку, равное числу определяемых коэффициентов (для уравнения (23)
- число связей, наложенных на выборку, равное числу определяемых коэффициентов (для уравнения (23) 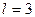 ).
).
Полученное разностное уравнение (25) модели считается адекватным объекту, если расчетное значение  больше некоторого критического значения
больше некоторого критического значения 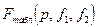 , т.е. при выполнении неравенства:
, т.е. при выполнении неравенства:
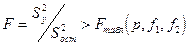 , (32)
, (32)
где 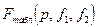 - критическое значение критерия, зависящее от чисел
- критическое значение критерия, зависящее от чисел 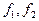 степеней свободы для дисперсии
степеней свободы для дисперсии 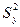 и
и 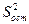
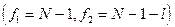 и от уровня значимости
и от уровня значимости 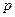 .
.
Критическое значение Фишера выбирается из таблиц распределения Фишера [4]. Уровень значимости принять равным 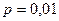 . При невыполнении условия (32) уравнение (25) модели не адекватно объекту.
. При невыполнении условия (32) уравнение (25) модели не адекватно объекту.
1.5 Алгоритм решения
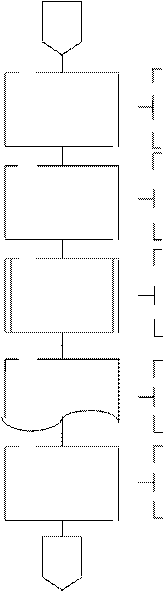
Алгоритм решения должен включать в себя выполнение следующих этапов (рис.4).
1. Вычисление коэффициентов разностного уравнения (18) имитационной модели объекта по параметрам непрерывной передаточной функции (7) по формулам (10)-(12).
2. Расчет переходного процесса по имитационной модели (18),(19) при единичном ступенчатом воздействии и определение параметров модели объекта МНК (идентификация).
3. Проверка адекватности полученной модели по критерию Фишера.
1
НАЧАЛО
2 Ввод исходных данных для
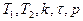 , имитационной модели объекта
, имитационной модели объекта
 и критерия Фишера
и критерия Фишера
Пересчет коэффициентов
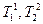 уравнения (6) по постоянным
уравнения (6) по постоянным
времени 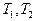 объекта
объекта
Расчет параметров дискретной
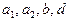 модели (18) с заданным тактом
модели (18) с заданным тактом 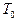
по формулам (10),(11),(12).
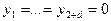 Задание нулевых
Задание нулевых
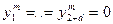 начальных условий
начальных условий
 Формирование единичного
Формирование единичного
 ступенчатого воздействия
ступенчатого воздействия
на вход объекта
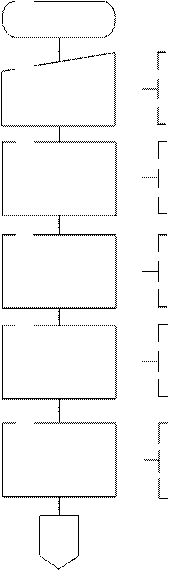
Рис. 4. Схема алгоритма решения задачи
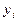 ,
, 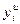 Расчет переходного процесса объекта
Расчет переходного процесса объекта
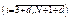 по имитационной модели без помехи
по имитационной модели без помехи
и с учетом помехи 
8 Вычисление сумм при искомых
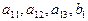 , коэффициентах и массива свободных
, коэффициентах и массива свободных
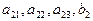 , членов
, членов 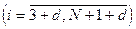
 системы уравнений (28)
системы уравнений (28)
9 Решение системы (28) уравнений
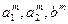 по правилу Крамера/методом Гаусса
по правилу Крамера/методом Гаусса
в соответствии с вариантом задания
относительно искомых коэфф.
 10
10
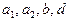 , Печать параметров имитационной
, Печать параметров имитационной
 модели (18) и коэффициентов
модели (18) и коэффициентов
восстановленной модели (23)
Расчет дисперсии относительно
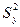 ,
, 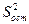 ,
,  среднего, остаточной дисперсии
среднего, остаточной дисперсии
и критерия Фишера
Рис. 4. Продолжение
12 Нет Проверка выполнения

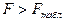 условия адекватности
условия адекватности
модели объекту
Да
Модель адекватна
объекту
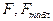 Модель
Модель
не адекватна
объекту
15 Печать переходных процессов объекта
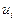 ,
, 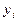 ,
, 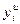 ,
, 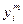 по имитационной модели без помехи,
по имитационной модели без помехи,
 с помехой и по восстановленной модели
с помехой и по восстановленной модели
при ступенчатом входном воздействии
КОНЕЦ
Рис.4. Окончание
2. Порядок выполнения работы
2.1 Изучить методические указания.
2.2 В соответствии с вариантом задания (графа 1 таблицы), полученным от преподавателя, выписать исходные данные и уяснить постановку задачи.
2.3 Составить алгоритм решения поставленной задачи, включающий:
а) расчет параметров разностного уравнения имитационной модели 1-го, 2-го или 3-го порядка (в зависимости от варианта задания (графы 4-6 таблицы)) и переходных процессов по имитационной модели при наличии помехи и без нее ( 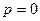 );
);
б) параметрическую идентификацию восстанавливаемой модели разностными уравнениями различных порядков (графа 11 таблицы) по переходным характеристикам имитационной модели при наличии помехи и без нее;
в) проверку адекватности полученных моделей по имитационной при наличии помехи и без нее.
2.4 Составить программу на языке 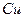 и провести расчеты на ПЭВМ.
и провести расчеты на ПЭВМ.
2.5 Провести анализ полученных результатов и сделать вывод о качестве идентификации модели уравнениями различных порядков при наличии помехи и без нее.
2.6 Оформить контрольную работу.
3. СОДЕРЖАНИЕ ОТЧЕТА
3.1 Наименование и цель работы.
3.2 Описание постановки задачи.
3.3 Математическая формулировка задачи.
3.4 Схема алгоритма решения.
3.5 Распечатка программы и результатов расчетов.
3.6 Графики переходных процессов объекта 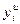 (при наличии помехи и без нее) и модели
(при наличии помехи и без нее) и модели 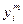 (разных порядков).
(разных порядков).
3.7 Анализ полученных результатов.
Варианты заданий
| № вари- | Технологический объект (ТО) | Канал объекта регулирования | Пар. мо- дели ТО |
| анта | Первая пост. врем. | ||

| |||
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 4,21 мин | |
| Колонна ректификации | Расход теплоносителя в кипятильник - содержание компонента смеси на к.т. | 81 мин | |
| Полимеризатор | Расход рассола в рубашку полимеризатора - температура смеси | 6 мин | |
| Колонна экстрактивной ректификации | Расход флегмы - содержание компонента смеси в дистилляте | 41,8 мин | |
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 8 мин | |
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 12 мин | |
| Паровой котел | Расход топлива - температура в котле | 153,5 с | |
| Полимеризатор | Расход рассола в рубашку полимеризатора - конверсия мономера | 78 мин | |
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 4,21 мин | |
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 3,59 мин | |
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 7,86 мин | |
| Колонна экстрактивной ректификации | Расход флегмы - содержание компонента смеси на в.к.т. | 11,7 мин | |
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 8 мин |
Таблица
к выполнению работы
| Параметры модели ТО | Такт кван- | Порядки уравне- | Метод решения | ||||||||
| Вторая пост. врем. | Третья пост. врем. | Коэффи-циент усиления | Время чистого запазд. | Коэф. поме-хи | това- ния | ний восстанав-ливаемых | системы лин. уравне- | ||||
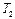
| 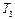
| 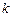
| 
| 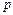
| 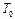
| моделей | ний | ||||
| - | - | 12,1 ºС/(т/ч) | 2,3 мин | 0,61 | 0,1 мин | 1;2 | Правило Крамера | ||||
| 27 мин | - | -5 %/(т/ч) | 27 мин | 0,25 | 1 мин | 1;3 | Метод Гаусса | ||||
| 2 мин | - | 4 ºС/(м3/ч) | 2 мин | 0,2 | 0,1 мин | 2;3 | Правило Крамера | ||||
| 15,3 мин | 10,2 мин | -5,81 %/(т/ч) | 16 мин | 0,29 | 2 мин | 1;2 | Метод Гаусса | ||||
| 2 мин | - | 1 ºС/(т/ч) | 3,8 мин | 0,05 | 0,2 мин | 1;3 | Правило Крамера | ||||
| 2,44 мин | - | 4,5 ºС/(т/ч) | 3 мин | 0,225 | 0,25 мин | 2;3 | Метод Гаусса | ||||
| 24 с | 15 с | 1,77 ºС/( м3/ч) | 0 с | 0,089 | 10 с | 1;2 | Правило Крамера | ||||
| 77 мин | - | 1,5 %/(м3/ч) | 6 мин | 0,075 | 2 мин | 1;3 | Метод Гаусса | ||||
| 3,19 мин | - | 12,1 ºС/(м3/ч) | 0,5 мин | 0,61 | 0,1 мин | 2;3 | Правило Крамера | ||||
| 2,8 мин | - | 7,3 ºС/(т/ч) | 4 мин | 0,37 | 0,5 мин | 1;2 | Метод Гаусса | ||||
| - | - | 3,05 ºС/(т/ч) | 2 мин | 0,15 | 0,25 мин | 1;3 | Правило Крамера | ||||
| 5,48 мин | 4,9 мин | -4,33 %/(т/ч) | 20 мин | 0,22 | 2 мин | 2;3 | Метод Гаусса | ||||
| 2 мин | - | 1 ºС/(м3/ч) | 2,1 мин | 0,05 | 0,1 мин | 1;2 | Правило Крамера | ||||
| № вари- | Технологический объект (ТО) | Канал объекта регулирования | Пар. мо- дели ТО | ||||||||
| анта | Первая пост. врем. | ||||||||||

| |||||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 73,84 мин | |||||||||
| Полимеризатор | Расход катализатора - температура в реакторе | 41,72 мин | |||||||||
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 4,21 мин | |||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 73,84 мин | |||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 35,18 мин | |||||||||
| Полимеризатор | Расход катализатора - вязкость выходного продукта | 45,45 мин | |||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - содержание компонента смеси в кубе кол. | 65 мин | |||||||||
| Теплообменник | Расход греющего пара - температура смеси на выходе теплообменника | 4,21 мин | |||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 73,84 мин | |||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 10,12 мин | |||||||||
| Колонна экстрактивной ректификации | Расход флегмы - содержание компонента смеси в дистилляте | 41 мин | |||||||||
| Колонна ректификации | Расход теплоносителя в кипятильник - температура смеси в кубе колонны | 12 мин | |||||||||
Продолжение таблицы
| Параметры модели ТО | Такт кван- | Порядки уравне- | Метод решения | ||||
| Вторая пост. врем. | Третья пост. врем. | Коэффи-циент усиления | Время чистого запазд. | Коэф. поме-хи | това- ния | ний восстанав- ливаемых | системы лин. уравне- |
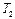
| 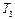
| 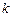
| 
| 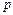
| 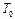
| моделей | ний |
| 15,13 мин | - | 0,08 ºС/(т/ч) | 10 мин | 0,04 | 1 мин | 1;3 | Метод Гаусса |
| 17,28 мин | - | -1,03 ºС/(м3/ч) | 8 мин | 0,052 | 1 мин | 2;3 | Правило Крамера |
| 3,19 мин | - | 12,1 ºС/(м3/ч) | 5 мин | 0,61 | 0,5 мин | 1;2 | Метод Гаусса |
| 15,13 мин | - | 0,08 ºС/(т/ч) | 15 мин | 0,04 | 1 мин | 1;3 | Правило Крамера |
| 2,88 мин | - | 1,04 ºС/(т/ч) | 9 мин | 0,052 | 1 мин | 2;3 | Метод Гаусса |
| 20,35 мин | - | 0,4 г/см3/(т/ч) | 12 мин | 0,02 | 1 мин | 1;2 | Правило Крамера |
| 40 мин | 15 мин | -0,9 %/(т/ч) | 10 мин | 0,045 | 2 мин | 1;3 | Метод Гаусса |
| - | - | 12,1 ºС/(м3/ч) | 7 мин | 0,61 | 0,5 мин | 2;3 | Правило Крамера |
| 15,13 мин | - | 0,08 ºС/(т/ч) | 8 мин | 0,004 | 1 мин | 1;2 | Метод Гаусса |
| 2,77 мин | - | 3,12 ºС/(т/ч) | 8 мин | 0,16 | 0,5 мин | 1;3 | Правило Крамера |
| 19,17 мин | 0,698 мин | -0,13 %/(т/ч) | 20 мин | 0,007 | 2 мин | 2;3 | Метод Гаусса |
| - | - | 2 ºС /(т/ч) | 2 мин | 0,2 | 0,2 мин | 1;2 | Правило Крамера |
Библиографический список
1. Баглаев Ю.П. Вычислительная математика и программирование. - М.: Высш. шк., 1990. С.312-322.
2. Изерман Р. Цифровые системы управления. – М.: Мир, 1984. С.58-72.
3. Кафаров В.В. Методы кибернетики в химии и химической технологии. – М.: Химия, 1985. С.72-73.
4. Львовский Е.Н. Статисти
|
из
5.00
|
Обсуждение в статье: Методические указания к выполнению контрольной работы по курсу «Цифровые многомерные системы управления», |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

