 |
Главная |
Методы построения функций принадлежности нечетких множеств
|
из
5.00
|
В классических множествах подмножества формируются так, что принадлежность элементов носителя этим подмножествам является абсолютной. Например, если носитель – множество действительных чисел, а подмножество – целые положительные числа, то все соответствующие точки носителя (1,2, 3, …) принадлежат этому подмножеству со степенью принадлежности 1.
Другое дело, если носитель – человеческий возраст, а подмножество этого носителя – «взрослые люди». Тогда эксперт, устанавливающий связь между множеством возрастов и подмножеством взрослых людей, может испытывать известные затруднения в ходе такой «мягкой» классификации. Может даже показаться, что такая классификация – дело сугубо субъективное. Однако в большинстве случаев дефиниции качественных понятий существует некая конвенциональная, разделяемая большинством человеческого сообщества, точка зрения, которая, к тому же, опирается на распространённые физические измерители. Так, «высокая температура» у человека начинается с 37 градусов по Цельсию, и с этим никто спорить не станет. Точно так же, понятие «оптимальный возраст работника» базируется на способности человека к долговременному труду, к накоплению и переработке информации и т. д., и эта способность снижается по мере старения. Все это дает основания для «мягкой» классификации.
Итак, нечёткое множество – это подмножество некоторого множества-носителя, принадлежность элементов носителя к которому устанавливается введенной экспертом или экспертным сообществом функцией принадлежности. Очень часто нечёткое множество применяется как инструмент установления связи между количественными данными и качественными классами, организованными на этих данных.
При использовании прямых методов построения функций принадлежности нечетких множеств эксперт либо просто задает для каждого 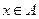 значение
значение 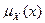 , либо определяет функцию совместимости. Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давления, температура и т.д., или когда выделяются полярные значения.
, либо определяет функцию совместимости. Как правило, прямые методы задания функции принадлежности используются для измеримых понятий, таких как скорость, время, расстояние, давления, температура и т.д., или когда выделяются полярные значения.
Во многих задачах при характеристике объекта можно выделить набор признаков и для каждого из них определить полярные значения, соответствующие значениям функции принадлежности, 0 или 1.
Например, в задаче распознавания лиц можно выделить следующие шкалы:
| х1 | Высота лба | низкий | широкий |
| х2 | Длина носа | короткий | длинный |
| х3 | Разрез глаз | узкие | широкие |
| х4 | Цвет глаз | светлые | темные |
| х5 | Форма подбородка | остроконечный | квадратный |
| х6 | Толщина губ | тонкие | толстые |
| х7 | Цвет лица | темный | светлый |
| х8 | Очертание лица | овальное | квадратное |
Для конкретного лица Х эксперт, исходя из приведенной шкалы, задает 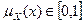 , формируя векторную функцию принадлежности
, формируя векторную функцию принадлежности 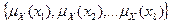 .
.
При прямых методах используются также групповые прямые методы, когда, например, группе экспертов предъявляют конкретное лицо, и каждый должен дать один из двух ответов: «этот человек лысый» или «этот человек не лысый», тогда количество утвердительных ответов, деленное на общее число экспертов, дает значение 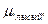 (данного лица).
(данного лица).
Косвенные методы определения значений функции принадлежности используются в случаях, когда нет элементарных измеримых свойств, через которые определяется интересующее нас нечеткое множество. Как правило, это методы попарных сравнений. Если бы значения функций принадлежности были нам известны, например, 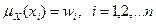 , то попарные сравнения можно представить матрицей отношений
, то попарные сравнения можно представить матрицей отношений 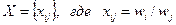 (операция деления).
(операция деления).
На практике сам эксперт формирует матрицу Х, при этом предполагается, что диагональные элементы равны 1, а для элементов симметричный относительно диагонали 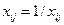 , т.е. если один элемент оценивается в α раз сильнее чем другой, то этот последний должен быть в 1/α раз сильнее, чем первый. В общем случае задача сводится к поиску вектора w, удовлетворяющего уравнению вида
, т.е. если один элемент оценивается в α раз сильнее чем другой, то этот последний должен быть в 1/α раз сильнее, чем первый. В общем случае задача сводится к поиску вектора w, удовлетворяющего уравнению вида 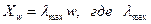 – наибольшее собственное значение матрицы Х. Поскольку матрица Х положительна по построению, решение данной задачи существует и является положительным.
– наибольшее собственное значение матрицы Х. Поскольку матрица Х положительна по построению, решение данной задачи существует и является положительным.
Экспертные оценки альтернативных вариантов по критериям могут быть представлены как нечеткие множества или числа, выраженные с помощью функций принадлежности. Для упорядочения нечетких чисел существует множество методов, которые отличаются друг от друга способом свертки и построения нечетких отношений. Последние можно определить как отношения предпочтительности между объектами. Рассмотрим одну из математических постановок задач принятия решений на основе теории нечетких множеств для поиска перспективного ассортимента оптового предприятия.
Методика выполнения
Конкретные примеры решения такого рода задач довольно громоздки ввиду объемных вычислений с использованием матриц больших размеров. На складах оптовых предприятий, например, могут находиться сотни наименований товаров одного профиля, эти предприятия осуществляют поставки десяткам потребителей – розничных магазинов. Для получения более или менее адекватной модели используется до двух десятков признаков, а построение функции принадлежности осуществляется с помощью нескольких экспертов, после чего производятся дополнительные «сглаживающие» вычисления.
В приведенной ниже задаче рассмотрен условный случай. Оптовое предприятие обслуживает всего четыре потребителя и поставляет им менее десяти наименований товаров. При оценке используются всего четыре признака.
Пример 2. Вычисление проводится для летнего сезона.
Дано Х= {x1, x2, x3, x4, x5, x6} – шесть наименований обувных товаров, имеющихся на складе оптового торгового предприятия или выдвигаемых в качестве коммерческих предложений, а именно: x1 –валенки; x2 – пляжные шлепанцы; x3 – резиновые сапоги; x4 – туфли из натуральной кожи; x5 – кроссовки; x6 – парусиновые туфли.
Y= {y1, y2, y3, y4} – множество признаков товаров, а именно; у1 – сезонность; у2 – цена; у3 – качество; у4 – внешний вид.
Z = {z1, z2, z3, z4} – множество розничных торговых предприятий, а именно: z1 – рынок; z2 – сетевой магазин; z3 – бутик; z4 – эконом.
Функции принадлежности нечетких бинарных отношений ξR : X x Y → [0, 1] и ψ: Y x Z → [0, 1] представляются в виде матриц R и S следующим образом:
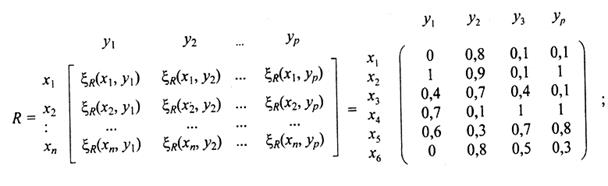
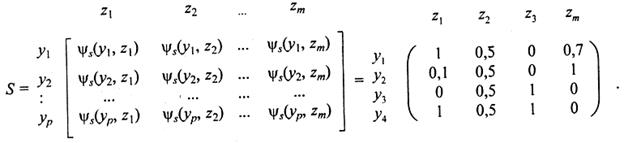
Определите перспективный ассортимент предприятия оптовой торговли, т.е. набор xj для удовлетворения предполагаемых запросов из Z.
Решение. Из матриц R и S получаем матрицу Т, элементы которой определяются по формуле
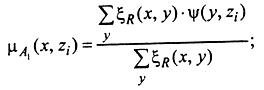
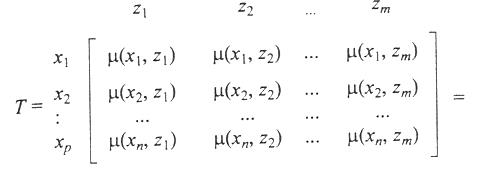

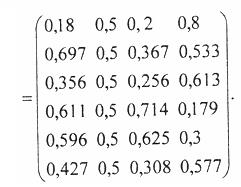
Далее строится матрица:
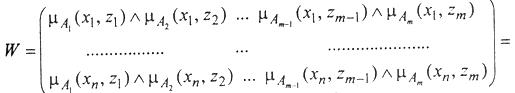
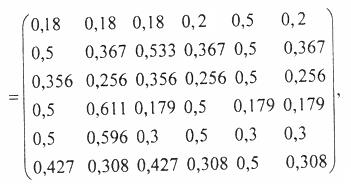
где ^ означает операцию попарного минимума.
Порог разделения l ассортимента ограничивается условием
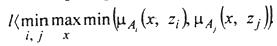
Для определения порога определяем максимальные значения μ в каждом из столбцов матрицы W. Это числа 0,5; 0,611; 0,533; 0,5 и 0,367. Следовательно, l < 0,367. Находим в матрице Т наибольшее значение, меньшее 0,367, и получаем 0,356. Итак, l = 0,356.
После того как порог l выбран, z определяется уровневое множество:
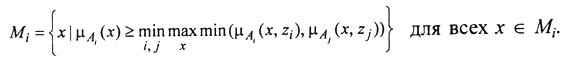
Ответ. М1 = {x2, x4, x5, x6}; М2 = {x1, x2, x3, x4, x5, x6}; М3 = {x2, x4, x5}; М4 = {x1, x2, x3, x6}.
Как видно из условия задачи, для потребителя z1 (рынок) наиболее важными характеристиками товаров являются сезонность и внешний вид. Поэтому в множество М1 попали товары ходовые, легко реализуемые летом и к тому же способные украсить витрину (шлепанцы, кожаные и парусиновые туфли, кроссовки). Сетевой магазин z2, ориентирующийся на самый широкий спектр покупателей и к тому же не стесненный в складских помещениях, готов принять любые товары из имеющихся на складе оптового предприятия. Относительно потребителей z3 и z4 выводы сделайте самостоятельно.
|
из
5.00
|
Обсуждение в статье: Методы построения функций принадлежности нечетких множеств |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

