Общие представления о колебательных спектрах многоатомных молекул

Число колебательных степеней свободы n в молекуле легко подсчитать по формулам (56) и (57). Казалось бы, что число основных полос в спектре поглощения должно соответствовать числу n. Эксперимент же показывает, что очень часто число основных полос меньше числа внутримолекулярных колебаний. Данные табл.4 иллюстрируют это на примере нескольких веществ.

 

Таблица 4. Число колебательных степеней свободы, число частот колебаний и число основных полос в ИК спектре поглощения некоторых многоатомных молекул

Молекула	Число колебательных степеней свободы	Число частот колебаний	Число основных полос в ИК спектре поглощения
H2O CO2 NH3 CH4 CHCl3	3∙3-6=3 3∙3-5=4 3∙4-6=6 3∙5-6=9 3∙5-6=9

 

Несовпадение числа полос в спектре поглощения с числом внутримолекулярных колебаний возможно по двум причинам (здесь и далее речь будет идти только об основных полосах поглощения).

Во-первых, как уже указывалось, некоторые колебания в многоатомных молекулах могут быть вырожденными, т.е. иметь одинаковую частоту колебаний. Если в молекуле несколько таких колебаний, то число различных частот по сравнению с числом колебаний будет меньше, а вся группа вырожденных колебаний даст в ИК спектре лишь одну основную полосу. Чем выше симметрия молекулы, тем больше степень вырождения и тем больше групп вырожденных колебаний.

Во-вторых, при различных колебаниях молекула обладает разной способностью к поглощению электромагнитной энергии. Согласно классической электродинамике поглощение электромагнитной энергии должно сопровождаться изменением осцилляции электрических зарядов в поглощающей среде. Поэтому ИК излучение могут поглощать только те молекулы, у которых при изменении расстояния между ядрами происходит смещение центров тяжести электрических зарядов, т.е. меняется дипольный момент:

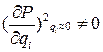(58)

При этом постоянный дипольный момент может быть равен нулю (например, неполярные молекулы CO₂, СН₄, ВF₃, C₆H₆ и т.п.).

 

Линейные и нелинейные трёхатомные молекулы ХУ₂

На рис. 16 приведены (схематически, без соблюдения масштаба) формы колебаний молекул СО₂ и H₂O. Молекула СО₂ линейная, в равновесном состоянии межъядерное расстояние r(С-0)=1.16∙10^-10 м. Число колебательных степеней свободы этой молекулы равно 4, однако два деформационных колебания имеют одинаковую частоту, т.е, дважды вырождены. Движение ядер в этом случае можно представить как суммарный результат колебаний в двух взаимно перпендикулярных плоскостях. Таким образом, молекула СО₂ имеет 3 частоты колебаний: ν₁=1388.17 (валентное симметричное), ν₂=667.4 (деформационное антисимметричное) и ν₃=2349.16 см^-1 (валентное антисимметричное).

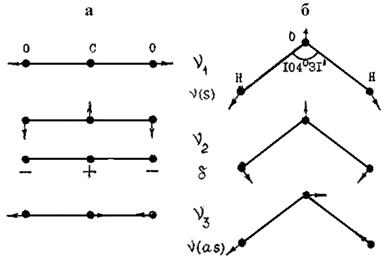
Рис. 16. Формы колебаний молекул СО₂ (а) и Н₂О (б)

 

Из них ν₂ и ν₃ удовлетворяют условию 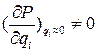, поэтому в ИК спектре поглощения СО₂ (рис. 17) наблюдаются две полосы, соответствующие частотам ν₂ и ν₃.

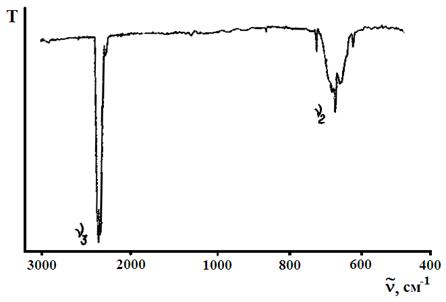
Рис. 17. ИК спектр поглощения СО₂.

 

Молекула Н₂О – нелинейная, в равновесном состоянии межъядерное расстояние r(О-Н)=0.957·10^-10 м, угол между связями 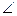НОН=104°31'. Вырождение колебаний для нее отсутствует, и число колебательных степеней свободы совпадает с числом частот колебаний: ν₁= 3656.65, ν₂=1594.78 и ν₃=3755.79 см^-1. Все три частоты удовлетворяют условию 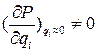и поэтому наблюдаются в ИК спектре поглощения.

 

Пирамидальные четырехатомные молекулы ХУ₃, ХУ₂Z.

Рассмотрим молекулу аммиака NH₃. Три атома водорода лежат в основании симметричной пирамиды, вершину которого занимает атом азота (рис. 18). В равновесном состоянии межсвязевый угол 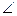HNH=107°17', а межъядерное расстояние r(N-H)=1.0156·10^-10 м.

 

 

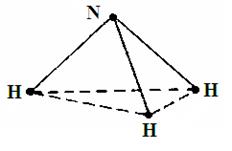
Рис. 18. Строение молекулы аммиака.

 

Число колебательных степеней свободы для этой молекулы равно 6, однако из-за симметричного строение два колебания являются дважды вырожденными, вследствие чего молекула NH₃, имеет только 4 колебательные частоты: ν₁=3336.68, ν₂=950.42, ν₃=3443.47 и ν₄=1627.75 см^-1. Все четыре частоты активны в ИК спектре поглощения, т.к. колебания удовлетворяют условию .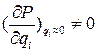

На рис.19 представлен ИК спектр поглощения NH₃, а формы колебаний молекулы – представлены схематически в табл. 5.

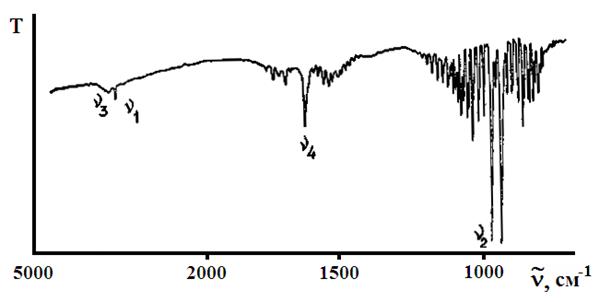
Рис. 19. ИК спектр поглощения аммиака.

 

Таблица 5. Колебания молекулы аммиака.

Частота	Схема формы колебания	Обозначение	Степень вырождения
ν1     ν2     ν3     ν4		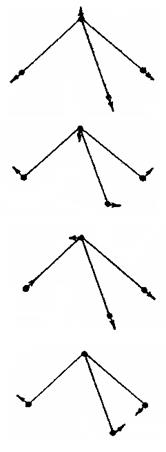ν(s)     δ(s)     ν(as)     δ(as)

 

Каждая полоса в ИК спектре NH₃ расщепляется на две вследствие так называемого "инверсионного удвоения". Последнее возникает в пирамидальных молекулах, для которых равновероятны две конфигурации (рис. 20а). Если потенциальный барьер между этими конфигурациями невелик, то молекула может переходить из одной в другую. В результате, каждый колебательный уровень расщепляется на два (положительный и отрицательный). В ИК спектре поглощения разрешены переходы между двумя уровнями различных знаков (рис.20б). Инверсионное расщепление наиболее заметно, для частот симметричных де­формационных колебаний.

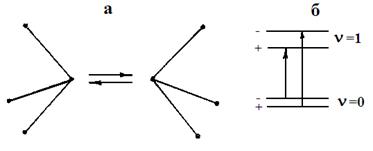
Рис. 20. Равновесные конфигурации молекулы аммиака (а); разрешенные колебательные переходы в ИК спектре поглощения (б)

 

Так же, как и в случае двухатомных молекул, колебательные переходы в многоатомных молекулах сопровождаются вращательными переходами. Если инфракрасный спектрофотометр обладает хорошей разрешающей способностью, то иногда в спектрах поглощения веществ в газовой фазе можно наблюдать тонкую структуру, обусловленную переходами между вращательными уровнями основного ( 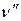=0) и вращательными уровнями возбужденного ( 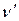=1) колебательного состояния. В отличие oт двухатомных молекул, в колебательно-вращательной полосе поглощения многоатомных молекул наряду с Р-ветвью (ΔJ=-1) и R-ветвью (ΔJ=+1) может наблюдаться также лежащая между ними Q-ветвь, соответствующая переходам с ΔJ=0 (рис. 21). Волновое число полосы в спектре определяют по положению Q-ветви, которая на вращательные линии не расщепляется. Если же: Q-ветвь не наблюдается, положение полосы определяют по "нулевой линии" между Р- и R-ветвями так же, как это делают в случае двухатомных молекул.

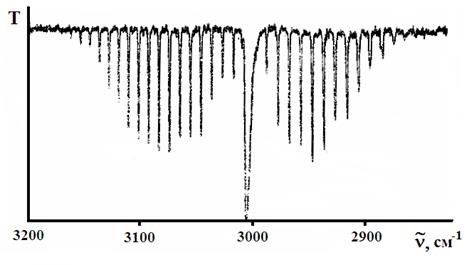
Рис. 21. Колебательно-вращательная полоса антисимметричного колебания газообразного метана.

 

Тот факт, что некоторые нормальные колебания многоатомных молекул проявляются в поглощении в виде колебательно-вращательных полос, с успехом используют для изучения вращательного движения этих молекул.

По волновым числам тонкой вращательной структуры, определяют вращательные постоянные и рассчитывают моменты инерции и геометрические параметры молекул исследуемого вещества. Особенно ценно, когда такая возможность представляется для неполярных молекул, чисто вращательные спектры поглощения которых, как известно, не наблюдаются.

Также как в двухатомной молекуле расстояние между соседними полосами в спектре 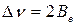, откуда можно определить вращательную постоянную В_е и, для наиболее простых случаев, момент инерции:

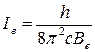(59)

Зная тип многоатомной молекулы и определив её момент инерции из вращательной постоянной, можно определить межъядерные расстояния в многоатомной молекуле ("Краткий справочник физико-химических величин" под. ред. Равделя, стр. 179, табл. 108).

Исследование колебательных спектров большого количества соединений позволило заметить, что некоторые частоты в ИК спектрах поглощения связаны с наличием в молекуле отдельных связей или групп атомов. Соответствующие полосы поглощения появляются в спектрах различных молекул, причем нередко сохраняется не только частота (в определенных пределах), но и (реже) интенсивность поглощения.

Полосы поглощения, характерные для определенной группы атомов и появляющиеся в определенной области частот ИК спектра, называются характеристическими полосами.

Характеристические частоты – частоты, которые характеризуют колебания определенной группы атомов и которые мало меняются при переходе от одной молекулы к другой.

Характеристичность по частоте приводит к появлению в спектре поглощения характеристических полос. Характеристические частоты и полосы имеют, например, группы СН, СН₂, СН₃, ОН, NH₂, NO₂, C=C, С≡С, С=0, ионы NO₃⁻, SO₄²⁻, NH₄⁺, РO₄³⁻ и т.д.

Пользуясь таблицами характеристических частот определённых групп атомов, можно определить наличие этих групп атомов в новой, неизвестной молекуле.

Практические работы

 

Работа №42, 49.

Контрольные вопросы:

1. Закон светопоглощения Ламберта-Бугера-Беера. Его определение и математическая формулировка. Понятия оптической плотности и процента пропускания, связь между ними. Коэффициент погашения, его физический смысл и экспериментальный способ определения.

2. Причины отклонений от закона Беера. Графическое выражение закона Бера.

3. Принцип определения константы диссоциации слабых электролитов в растворах спектрофотометрическим способом. Вид спектра поглощения слабой кислоты в зависимости от рН раствора.

4. Аналитический способ обработки экспериментальных данных: определение степени диссоциации слабой кислоты по поглощению аниона и по поглощению недиссоциированной кислоты. Расчёт рК_с по этим данным.

5. Графический метод определения рК_с.

 

Страницы для подготовки: 3-13

Задание 1. Определение константы диссоциации бромкрезолового зелёного в водном растворе. Рабочий диапазон рН от 3.0 до 9.0.

Структурная формула бромкрезолового зелёного:

 

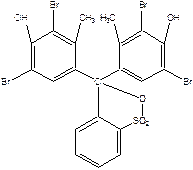
Задание 2. Определение константы диссоциации бромкрезолового пурпурного в водном растворе. Рабочий диапазон рН от 3.0 до 12.0.

Структурная формула бромкрезолового пурпурного:

 

 

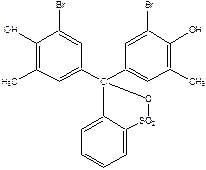
Порядок выполнения работы.

1. Приготовьте 10 растворов исследуемого вещества в указанном диапазоне рН. Для соседних растворов соблюдайте условие: .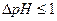

Для приготовления каждого раствора возьмите 3 мл стандартного раствора вещества (его концентрация указана на склянке) и добавьте 7 мл буферного раствора с определенным значением рН. Рассчитайте и запишите полученную при этом концентрацию исследуемого вещества в рабочих растворах.

Готовьте растворы как можно тщательнее. Результат работы в значительной степени будет определяться тем, насколько точно выдержана концентрация рабочих растворов.

2. На одном бланке запишите спектры поглощения всех приготовленных растворов. Запись проводится на спектрофотометре СФ-18.

Условия записи

- толщина поглощающего слоя - 1 см;

- скорость записи - 270 нм/мин.

3. Нанесите на полученные спектры значения рН для каждой кривой поглощения и определите, какая из полос относится к молекулярной форме вещества, а какая – к анионной.

Запишите реакцию диссоциации исследуемого вещества в растворе и укажите, в какую сторону смещено равновесие диссоциации в кислой и щелочной средах. На основании рассмотрения спектров поглощения объясните изменение цвета при переходе от низких к высоким значениям рН (цвета видимого спектра и их распределение по длинам волн указаны в приложении 1).

Определите по диаграмме оптические плотности А всех растворов при двух длинах волн, соответствующих максимумам поглощения.

 

Обработка экспериментальных данных и расчеты

1. На одном графике постройте кривые зависимости оптической плотности А от рН для двух длин волн. Определите величину рК графическим методом (см. стр. 12, рис. 6).

2. Для 3-4 растворов, расположенных в середине рабочего диапазона рН (т.е. там, где оптическая плотность сильно меняется при изменении рН), рассчитайте аналитически значения степени диссоциации α и рК_с .

Расчет ведется по следующим формулам:

- при длине волны λ₁, отвечающей максимуму полосы поглощения молекулы НА:

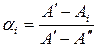(60)

- при длине волны λ₂, отвечающей максимуму полосы поглощения аниона А⁻:

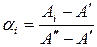(61)

Здесь 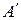- предельная оптическая плотность при низких значениях рН (молекулярная форма), 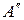- предельная оптическая плотность при высоких значениях рН (анионная форма), 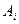- оптическая плотность раствора, для которого производится расчет степени диссоциации .

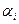Например, для системы, изображенной на рис. 22, степень диссоциации раствора с рН = 5 можно рассчитать как по полосе поглощения при λ₁, так и по полосе поглощения при λ₂.

При λ₁: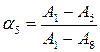

При λ₂: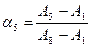

Подстрочные индексы в этих выражениях обозначают рН соответствующего раствора.

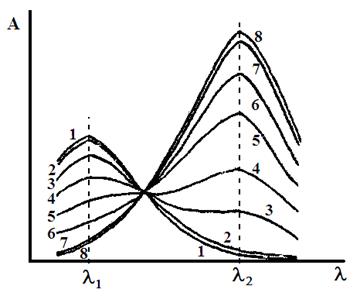
Рис.22. Спектры поглощения слабой кислоты в растворе при разных рН. Максимум поглощения недиссоциированных молекул НА при λ₁, анионов А⁻ – при λ₂

 

Естественно, что величины α, рассчитанные для одного и того же раствора при равных λ, должны быть близки.

Величина рК_с, соответствующая кажущейся или концентрационной (так называемой "функции концентрации") константе диссоциации К_с, рассчитывается по формуле:

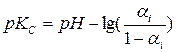(62)

Результаты расчета сведите в таблицу по образцу:

Таблица

рН	λ1	λ2
А	α	рКс	А	α	рКс

 

Рассчитайте среднее значение рК_с и сопоставьте его с величиной, полученной графическим способом. Выведите средний результат.

Приложение 1.

Распределение цвета по длинам волн в видимом спектре

400-420 нм Фиолетовый 560-600 нм Желтый

420-450 нм Синий 600-650 нм Оранжевый

450-490 нм Голубой 650-750 нм Красный

490-560 нм Зеленый

Работа №47

Контрольные вопросы:

1. Сколько колебаний может совершать линейная и нелинейная многоатомная молекула?

2. Какие колебания называются валентными, а какие – деформационными?

3. Причины уменьшения полос поглощения в ИК-спектрах по сравнению с числом колебаний. Вырождение.

4. Понятие о вращательных спектрах поглощения многоатомных молекул. Классификация многоатомных молекул по моментам инерции.

5. Определение теплоёмкости молекулы статистическим методом. Поступательный и вращательный вклады в теплоёмкость. Определение колебательного вклада в теплоёмкость, используя колебательные спектры и учитывая вырождение колебаний.

 

Страницы для подготовки: 17, 18, 25-32

 

Задание 1. Изучение ИК спектра поглощения газообразного аммиака. Определение частот внутримолекулярных колебаний и межъядерного расстояния r_NH в молекуле аммиака.

 

1. Заполните аммиаком газовую кювету с толщиной поглощающего слоя – 10 см. Заполнение производятся под тягой. Аммиак получают из аммиачной воды. Выделяющийся при нагревании аммиачной воды газ пропускают через осушительную колонку.

2. Произведете запись спектра поглощения газообразного аммиака на спектрофотометре ИКС-21.

Условия записи.

Область спектра – 650-4000 см^-1.

 

Особое внимание при этом следует обратить на область 1200-800 см^-1, где должна проявиться полоса, состоящая из двух четких максимумов Q-ветви и тонкой вращательной структуры Р- и R-ветвей.

3. Считая, что волновое число основной полосы примерно равно волновому числу соответствующего внутримолекулярного колебания, определите частоты внутримолекулярных колебаний NH₃. В случае инверсионного удвоения полосы её волновое число определяется как среднее арифметическое между волновыми числами двух максимумов, отвечающих Q-ветви.

4. Пользуясь данными "Краткого справочника физико-химических величин" (под. ред. Равделя, стр. 182, табл. 110), сопоставьте полученные данные с табличными и сделайте отнесение полос поглощения к определенным типам колебаний в молекуле.

5. Найдите в спектре полосу, отвечающую деформационным симметричным колебаниям в молекуле NH₃. Внимательно рассмотрите ее тонкую структуру и обозначьте Р-, R- и Q-тветви. Обратите внимание на инверсионное удвоение полосы. Определите среднее значение разности волновых чисел соседних линий 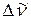тонкой вращательной структуры. Для этого удобно взять 3-4 ближайших к Q-ветви линий в Р- и R-ветвях полосы.

6. Рассчитайте величину вращательной постоянной как 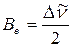и момента инерции 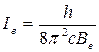молекулы NH₃.

7. Рассчитайте межъядерное расстояние r_NH, учитывая, что молекула NH₃ относится к типу симметричного волчка, для которого 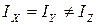. Для расчета r_NH воспользуйтесь формулой для момента инерции 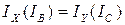, приведенной в "Кратком справочнике физико-химических величин" (под. ред. Равделя, стр. 179, табл. 108). Угол α между связью N-Н и осью симметрии (высотой пирамиды) составляет 73⁰10'.

8. Сопоставьте рассчитанное значение межъядерного расстояния r_NH c табличным.

 

Задание 2. Изучение ИК спектра поглощения газообразного метана. Определение частоты валентного антисимметричного колебания и равновесного межъядерного расстояния r_СН в молекуле

 

1. Произведете запись спектра поглощения газообразного аммиака на спектрофотометре UR-10.

2. Внимательно рассмотрите полученную диаграмму. Найдите и обозначьте Р-, R- и Q-ветви полосы поглощения; найдите тонкую вращательную структуру полосы

3. По положению Q-ветви определите волновое число полосы поглощения, соответствующей антисимметричному валентному колебанию. Сопоставьте полученную величину со справочными данными.

4. Определите разность волновых чисел 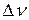соседних линий вращательной структуры в Р-ветви. Для этого удобно взять 8-10 соседних линий и определить разность волновых чисел двух крайних линий, а затем полученную разность разделить на число интервалов между линиями.

5. Рассчитайте момент инерции и равновесное межъядерное расстояние в молекуле метана, исходя из того, что эта молекула представляет собой правильный тетраэдр о углом Н-С-Н между связями, равным 109°28', и относится к типу сферического волчка. Для расчета r_CH воспользуйтесь формулой для момента инерции, приведенной в "Кратком справочнике физико-химических величин" (под. ред. Равделя, стр. 179, табл. 108).

6. Сопоставьте полученное значение межъядерного расстояния с табличными.

Работа №51.

Контрольные вопросы:

1. Превращение энергии при поглощении и причина появления полосы поглощения в спектре.

2. Вращательные спектры поглощения двухатомных молекул. Их внешний вид и механизм возникновения. Вращательная энергия и вращательный терм. Вращательная постоянная. Модель “жёсткого ротатора” для определения межъядерных расстояний по вращательным спектрам поглощения. Выражение для собственных значений вращательной энергии.

3. Колебательные спектры поглощения двухатомных молекул. Модель “гармонического осциллятора” для анализа колебательных спектров поглощения. Энергия колебательного движения. Смысл колебательной постоянной. Кривая потенциальной энергии и колебательные уровни. Правило отбора и количество полос в спектре.

4. Основные недостатки модели “гармонического осциллятора”. Модель “ангармонического осциллятора”. Кривая потенциальной энергии и колебательные уровни. Энергия колебательного движения. Правило отбора и вид колебательного спектра.

5. Определение колебательной постоянной, коэффициента ангармоничности, числа колебательных уровней и энергии диссоциации по колебательному спектру поглощения.

6. Колебательно-вращательные спектры поглощения двухатомных молекул. Их вид и природа их возникновения. Определение вращательной постоянной, момента инерции и равновесного межъядерного расстояния по колебательно-вращательному спектру.

 

Страницы для подготовки: 13-25

 

Задание 1. Изучение спектра поглощения газообразного хлористого водорода. Определение волнового числа основного тона и равновесного межъядерного расстояния в молекуле HCI.

Порядок выполнения задания

1. Произведите запись спектра поглощения газообразного НСl в области 2500-3200 см^-1 (основной тон).

Условия записи: масштаб регистрации – 32 мм/100 см^-1; скорость регистрации – 50 cм^-1/мин; щелевая программа – 2.

2. Проведите обработку полученных экспериментальных данных, как описано ниже в разделе "Обработка экспериментальных данных и расчеты".

 

Задание 2. Изучение спектра поглощения газообразного оксида углерода. Определение волнового числа основного тона и равновесного межъядерного расстояния в молекуле СО.

Порядок выполнения задания

1. Произведите запись спектра поглощения СО в области 2000-2250 см^-1 (основной тон).

Условия записи: масштаб регистрации – 150мм/см^-1; скорость регистрации – 42 см^-1/мин; щелевая программа – 2.

2. Проведите обработку полученных экспериментальных данных, как описано ниже в разделе "Обработка экспериментальных данных и расчеты".

 

Обработка экспериментальных данных и расчеты

1. Внимательно рассмотрите полученную запись спектра. Найдите и обозначьте Р- и R-ветви полосы поглощения; рассмотрите вращательную структуру каждой полосы.

2. Пронумеруйте все линии вращательной структуры, отсчитывая от центра полосы, где нет поглощения (1,2,3 и т.д. для R-ветви и -1,-2,-3 и т.д. для Р-ветви).

3. Определите волновое число максимума каждой линии вращательной структуры в Р- и R-ветвях, отнесите каждую линию к определен­ному переходу между вращательным уровнем нижнего колебательного состояния и вращательным уровнем верхнего колебательного состояния. Данные занесите в таблицу по следующему образцу:

 

Таблица

Волновые числа вращательных линий колебательно-вращательного спектра поглощения газообразного ______

 

Р-ветвь	R-ветвь
J	x=-J	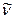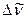, см-1	, см-1	J	x=J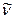+1	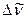, см-1	, см-1
	-1 -2 -3

 

Обозначения: J – вращательное квантовое число нижнего уровня; х – номер линий во вращательной структуре; 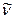- волновое число линии в спектре; 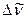- разность волновых чисел соседних линий в ветви.

4. Определите приближенно волновое число основного колебательного перехода 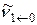по положению нулевой линии, взяв среднее арифметическое значение из волновых чисел двух ближайших к центру полосы линий, одной в Р-ветви, другой – в R-ветви.

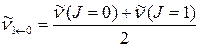(63)

5. Учитывая приближение модели жёсткого ротатора, рассчитайте величину равновесного межъядерного расстояния.

а) Рассчитайте средние величины вращательной постоянной В_е и момента инерции. Для этого определите среднюю разность волновых чисел между двумя соседними линиями, используя 4-5 ближайшие к центру полосы в Р- и R-ветви. Из соотношения 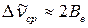найдите среднюю величину вращательной постоянной В_е.

б) Рассчитайте момент инерции I_e и межъядерное расстояние r_e в молекуле (формулы (27) и (32), стр. 14).

6. Сопоставьте рассчитанные молекулярные константы B_e, I_e, r_e, а также волновое число основного перехода 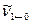со справочными данными.

 

Дополнительные задания

Расчет сумм состояний и распределения молекул по вращательным и колебательным уровням

1. Рассчитайте вращательную сумму состояний Q_r при температуре, указанной преподавателем:

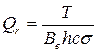(64)

где фактор симметрии σ=1

2. Рассчитайте долю общего числа молекул на каждом из первых одиннадцати (включая нулевой) вращательных уровнях при температуре, указанной преподавателем.

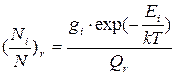, (65)

где степень вырождения g=2J+1.

3. Постройте график зависимости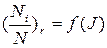

4. Рассчитайте колебательную сумму состояний Q_ν при Т = 298 и 1000 К приняв, что волновое число основного тона равно колебательной постоянной: .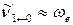

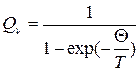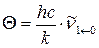, где (66)

5. Рассчитайте долю общего числа молекул при 298 и 1000 К на нулевом и первом колебательных уровнях. При этом не следует забывать, что Е_кол на нулевом уровне не равна нулю, но энергия колебаний ни любом другом уровне отсчитывается от нулевого. Колебании ядер на нулевом и первом уровнях можно считать гармоническими

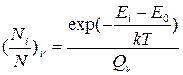(67)

6 Постройте график зависимости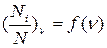

[1] Здесь и далее слова "свет", "световой" и т.п. условно используются для обозначения электромагнитного излучения не только в видимой, но и в других областях спектра, применяемых в молекулярной спектроскопии

[2] Закон светопоглощения был установлен экспериментально П.Бугером в 1729 г., математически сформулирован И.Ламбертом в 1760 г. и в отношении концентрации подтвержден А.Беером в 1852 г.

[3] Разрешающая способность характеризует способность данного прибора дать раздельное изображение двух близколежащих линий в спектре.