 |
Главная |
Расчет допусков размеров, входящих в размерные цепи
|
из
5.00
|
Размерная цепь – совокупность размеров, расположенных по замкну-тому контуру и участвующих в решении поставленной задачи.
Звенья размерной цепи называются составляющими звеньями и обозначаются прописными буквами русского алфавита (А, Б, В и т. д.).
Замыкающее (исходное) звено – звено, размер которого получается последним в результате обработки детали или сборки узла. Замыкающее звено в размерной цепи всегда одно, обозначается АΔ, БΔ, ВΔ.
Увеличивающее звено – звено размерной цепи, которое при своем увеличении увеличивает замыкающее звено, обозначается Аув., Б ув., В ув или  .
.
Уменьшающее звено – звено размерной цепи, которое при своем увеличении уменьшает замыкающее звено, обозначается Аум., Б ум., В ум. или 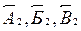 .
.
Известны пять методов достижения точности замыкающего звена:
1) метод полной взаимозаменяемости;
2) неполной взаимозаменяемости;
3) метод регулирования;
4) метод пригонки;
5) метод групповой взаимозаменяемости.
Размерный анализ обычно включает в себя решение двух задач: прямой и обратной. Прямая задача решается на стадии проектных расчетов, обратная – на стадии проверочных расчетов.
Исходные (замыкающие) размеры, определяющие точность относительного расположения деталей, выявляют по сборочным чертежам изделия, техническим требованиям к ним и др. нормативным материалам. В качестве замыкающего (исходного) звена может выступать зазор между поверхностями деталей, расстояние между осями или точками, угол между осями.
На рисунке 5.1 представлены размерные цепи Р и В червячного редуктора, где исходным (замыкающим) звеном РΔ является расстояние между средней плоскостью зубчатого червячного венца колеса и осью червяка, а ВΔ – осевой зазор между торцом крышки и кольца подшипника.
На рисунке 5.2 представлены размерные цепи А и Н, где исходными (замыкающими) звеньями являются зазоры между торцами деталей.
При методе полной взаимозаменяемости точность замыкающего звена обеспечивается у всех без исключения изделий без какого-либо подбора звеньев или их пригонки.
Алгоритм расчета размерной цепи методом полной взаимозаменяемости представлен в таблице 5.1.

Рисунок 5.1 – Размерные цепи червячного редуктора

а – цепь А; б – цепь Н
Рисунок 5.2 – Размерные цепи редукторов
Таблица 5.1 – Алгоритм расчета размерной цепи методом максимума и минимума (полной взаимозаменяемости)
| Расчетный параметр | Расчетная формула |
| 1 Записать параметры замыкающего звена: номинальное значение, предельные отклонения, допуск, координату середины поля допуска | АΔ; ЕSАΔ; EIАΔ;

|
| 2 Выявить размерную цепь, увеличивающие и уменьшающие звенья. Составить ее схему | По чертежу изделия |
| 3 Конструктивно определить номинальные значения составляющих звеньев | По чертежу изделия |
| 4 Проверить правильность определения номинальных значений составляющих звеньев | 
|
| 5 Определить среднее значение допусков составляющих звеньев | 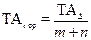
|
Окончание таблицы 5.1
| 6 По номинальным размерам составляю-щих звеньев, используя ГОСТ 25347–82 (таблица А.18), назначить допуски на все звенья, близкие к среднему значению, кроме одного звена* | 
|
| 7 Проверить правильность корректировки допусков и рассчитать допуск неизвестного звена путем вычитания из допуска замыкающего звена суммы допусков всех составляющих звеньев (пункт 6) | ТАΔ = ΣТАi |
| 8 Задать расположение допусков составляющих звеньев и записать их предельные отклонения, кроме одного звена | Для звеньев, определяющих размеры охватывающих поверхностей
 Для звеньев, определяющих размеры охватываемых поверхностей
Для звеньев, определяющих размеры охватываемых поверхностей

|
| 9 Определить координаты середин полей допусков, кроме одного звена | 
|
| 10 Определить координату середины поля допуска оставшегося неизвестным звена (при расчетах учитывать знаки координат) | 
|
| 11 Определить предельные отклонения оставшегося неизвестным звена | 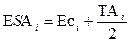 ; ;

|
| 12 Записать результаты расчетов: номинальные значения и найденные предельные отклонения составляющих звеньев | А1 =…; А2 =…; А3 =…; Аm-1 =… |
| 13 Проверить правильность расчетов |  
 
|
| Примечание – * – при наличии в размерной цепи стандартных изделий или деталей (подшипников, шпонок и т. п.) в процессе корректировки допусков на них следует устанавливать допуски, предусмотренные соответствующими стандартами |
Задача 1.Выявить размерную цепь по заданному чертежу сборочной единицы. Методом максимума и минимума определить допуски и предельные отклонения составляющих звеньев. Выполнить проверку правильности расчетов. Исходные данные взять из таблицы 5.2 и рисунка 5.3.
Таблица 5.2 – Варианты заданий к задаче 1
| Номер варианта | ||||||||
| Номер рисунка | 5.3, а | 5.3, б | 5.3, в | 5.3, г | 5.3, д | 5.3, ж | 5.3, з | 5.3, и |
| АΔ | 2-0,36 | 2±0,3 | 1±0,2 | 0+0,4 | 0+0,5 | 1+0,6 | 2-0,4 | 1-0,6 |
Продолжение таблицы 5.2
| Номер варианта | ||||||||
| Номер рисунка | 5.3, и | 5.3, ж | 5.3, з | 5.3, а | 5.3, б | 5.3, в | 5.3, г | 5.3, д |
| АΔ | 0+0,2 | 2±0,2 | 1±0,3 | 2±0,4 | 2-0,6 | 1+0,5 | 0+0,3 | 0+0,8 |



Рисунок 5.3 – Эскизы сборочных единиц для расчета размерных цепей
|
из
5.00
|
Обсуждение в статье: Расчет допусков размеров, входящих в размерные цепи |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

