 |
Главная |
С косозубым зацеплением
|
из
5.00
|
Рассчитать зубчатую передачу редуктора по данным примера 1. Вид зацепления зубьев – косозубое.
Расчет косозубой передачи проводится подобно расчету прямозубой передаче. Но есть некоторые изменения.
   |

а) б)
Рис.3. а - косозубые колеса в зацеплении б - схематическое изображение косозубого колеса
ПРОЕКТНЫЙ РАСЧЕТ
В колесах с косым зубом различают окружной шаг рt, который измеряется параллельно торцу колеса, и нормальный шаг pn, измеряемый в нормальном к направлению зуба сечении.
pn = рt cosβ,
где β – угол наклона линии зуба. Во избежание больших осевых усилий принимают β = 80…150 (редко 200).
Аналогично связаны между собой нормальный mn и окружной модули mt.:
mn = mt cosβ
По стандарту обычно выравнивают нормальный модуль.
1.1. Определение геометрических параметров зубчатой передачи.
Согласно правилам проектирования, вычисляем ориентировочное значение нормального модуля:
mn = (0,01…0,02)×a = (0,01…0,02)× 280 = 2,8…5,6мм.
По таблице стандартных значений модулей (табл.9.1[1]) принимается наименьший модуль из выбранного интервала (в отличие от прямозубого зацепления).
Принимаем среднее значение угла наклона зубьев b=150
Рассчитываем суммарное число зубьев ([1], формула 9.4):
 180,3»180;
180,3»180;
числа зубьев шестерни и колеса находим решением системы уравнений:
 ;
;
z1 = 180/(1+4)≈36;
z2 =180 – 36= 144;
проверяем передаточное число:
 ;
;
погрешность передаточного числа:
 0%,
0%,
что соответствует условиям ([1], табл.9.2 п.3 примечаний).
Определяем окончательно значение угла наклона зубьев:
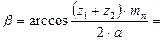 15о35′45′′. или
15о35′45′′. или
cosβ = (z1+z2) mn / 2а = 0,9643 →β = 15о35′85′′
Торцевой модуль:
 3,111 мм.
3,111 мм.
Делительные диаметры:
d1 = mt z1=mn×z1/ cosβ = 3,111×36= 111,996 мм;
d2 = mt z2=mn×z2/ cosβ = 3,111×144= 447,984 мм.
Проверка межосевого расстояния:
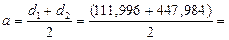 279,99 мм.
279,99 мм.
Полученные геометрические параметры косозубой передачи заносим в таблицу 3.1.
Таблица 1.1. Геометрические размеры цилиндрической зубчатой передачи
| Название | Межо севое расстояние а, мм | Модуль m, мм | Число зубьев z | Угол наклона зубьев, b0 | Ши рина зубчатого венца b, мм | Диаметры, мм | ||
| d | dа | df | ||||||
| Шестерня | 15о35′45′′ | 111,996 | 117,996 | 119,496 | ||||
| Колесо | 447,984 | 453,984 | 455,484 |
КИНЕМАТИЧЕСКИЙ РАСЧЕТ
Кинематический расчет редуктора с косозубой зубчатой передачей проводим по методике примера №1.
2.1. Допускаемое контактное напряжение рассчитывают следующим образом:
Для непрямозубых передач в качестве допускаемого контактного напряжения принимается условно допускаемое контактное напряжение, определяемое по формуле ([1], формула 9.11):
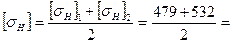 505,5 МПа.
505,5 МПа.
При этом должно выполняться условие:
[sН] £ 1,25×[sН]min ,
где [sН]min –меньшее из значений [sН]2 и [sН]1 :
1,25×[sН]min = 1,25×479 = 599 МПа.
Это условие выполняется:
[sН] = 505,5 МПа < 1,25×[sН]min = 599 МПа,
Поэтому для дальнейшего расчета принимается [sН] = 505,5 МПа.
2.2. Расчет крутящего момента.
Расчет крутящего момента на колесе (для косозубых передач) ведем по наименьшему допустимому напряжению: [sН ]=479 МПа по формуле 9.39 [1]:
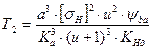 , Н∙мм;
, Н∙мм;
где КHb –коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба и принимаемый в зависимости от ψва (табл. 9.17 [1]). Принимаем КHb = 1,1.
Ка – коэффициент межосевого расстояния, учитывающий вид зацепления зубьев. Ка = 43 для косозубых передач.
 = 3283887,9 Н∙мм.
= 3283887,9 Н∙мм.
2.3. Расчет частоты вращения и угловой скорости выходного вала, расчет мощности выходного вала и выбор двигателя ведется по методике примера 1.
По расчетным данным составляется таблица 2.1.
Таблица 2.1. Выбор двигателя и определение передаточных чисел.
| Типоразмер двигателя | Р, кВт | nс, мин-1 | S | nдв, мин-1 | Uобщ | uдоп | Вывод |
2.4. Вывод.
Некоторые требования к цилиндрическим передачам [2]
1. Количество зубьев шестерни должно быть не меньше, чем zmin=17.
2. Модуль зацепления для силовых передач (то есть таких, которые передают мощность) m³1,5 мм. Модуль является такой величиной, которая должна быть стандартной во всех случаях без исключения.
3. Число зубьев колеса и шестерни не должно быть кратным друг другу, если они изготовлены из мягкой стали (НВ<350). В том случае, когда хоть одно из колес в паре имеет НВ≥350, то это требование отменяется. Поэтому в таблицах стандартов есть примечание, согласно которому допускается определенное отклонение передаточного числа от целого числа.
4. Допустимая перегрузка по контактным напряжением составляет 5%, а недогрузка – 10%, то есть: 0,9[sH]×≤ sH ≤ 1,05[sH]. ××Во всех других случаях передача является такой, которая не может быть определена как рассчитанная правильно.
5. В расчетах закрытых передач преимущество следует предоставлять таким передачам, которые имеют меньший модуль, чтобы только он равнялся или был больше 1,5 мм
6. Числа зубьев колес обязательно должны быть целыми.
7. При расчетах суммарного числа зубьев пары зацепления зубчатых прямозубых колес по формуле:  (z∑ – суммарное число зубьев; а – межосевое расстояние; m – модуль зацепления) нужно подобрать такой модуль, чтобы z∑ было целым числом. Это требование касается только прямозубих передач.
(z∑ – суммарное число зубьев; а – межосевое расстояние; m – модуль зацепления) нужно подобрать такой модуль, чтобы z∑ было целым числом. Это требование касается только прямозубих передач.
8. Тригонометрические функции необходимо считать до шестого знака (не переводя в минуты и секунды), линейные размеры – до четвертого знака после запятой.
|
из
5.00
|
Обсуждение в статье: С косозубым зацеплением |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

