Общая постановка задачи устойчивости по А.М. Ляпунову

Впервые строгое определение устойчивости было дано русским ученым А.М. Ляпуновым в 1892г.

Пусть движение системы автоматического управления описывается дифференциальными уравнениями, которые могут быть приведены к виду

, (3.1)

где 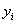– вещественные переменные, характеризующие состояние системы управления; – известные функции переменных 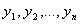и времени 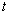, удовлетворяющие условиям существования и единственности решения.

Исходное состояние системы при однозначно определяется начальными значениями переменных 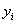, которые обозначим .

Каждой совокупности начальных значении соответствует единственное решение (3.1) для всех t> to

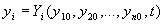. (3.2)

Решение (3.2) описывает какое-либо движение системы, определяемое исходным состоянием.

Некоторое вполне определенное движение системы, подлежащее исследованию на устойчивость, называют невозмущенным движением.

Заметим, что выбор невозмущенного движения является произвольным. Это может быть любое возможное движение системы, как установившееся, так и неустановившееся. Допустим, что в качестве невозмущенного движения выбрано такое, которое описывается заданными функциями времени

, ,…, .

Предположим, что функции являются частным решением дифференциальных уравнений (3.1), т. е.

, (3.4)

удовлетворяющим начальным условиям при

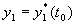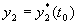, ,…, . (3.5)

В частном случае, когда параметры системы не изменяются со временем и функции не зависят явно от , движения (3.3) являются установившимися. Им отвечают решения 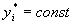, служащие корнями уравнений .

Изменим условия (3.5) дав начальным значениям переменных 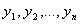небольшие по модулю приращения 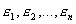, т. е. пусть при

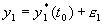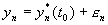, ,…, . (3.8)

Движение системы, отвечающее измененным начальным условиям (3.8), называют возмущенным движением. Другими словами, возмущенным движением системы называют всякое иное движение системы, отличное от невозмущенного.

Введем новые переменные , (3.9)

равные разности переменных 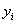в возмущенном и невозмущенном движении. Переменные называют отклонениями или вариациями величин .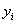

Если все отклонения равны нулю, то возмущенное движение будет совпадать с невозмущенным движением.

Пусть при переменные принимают какие-либо свои начальные значения , из которых, по крайней мере, одно не равно нулю

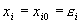. (3.11)

Начальные значения отклонений (3.11) называют возмущениями.

А. М. Ляпуновым было дано следующее определение устойчивости. Невозмущенное движение называют устойчивым по отношению к переменным , если при всяком произвольно заданном положительном числе , как бы мало оно ни было, можно выбрать другое такое положительное число , что при всяких возмущениях , удовлетворяющих условию

, (3.12)

и при любом t > to будет выполняться неравенство

,

в противном случае движение неустойчиво.

Практически устойчивость данного невозмущенного движения означает, что при достаточно малых начальных возмущениях возмущенное движение будет сколь угодно мало отличаться от невозмущенного движения. Если же невозмущенное движение неустойчиво, то возмущенное движение будет отходить от него, как бы малы ни были начальные возмущения.

Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, т. е.

, (3.14)

то невозмущенное движение называют асимптотически устойчивым.

При асимптотической устойчивости изображающая точка с течением времени должна неограниченно стремиться к началу координат, не выходя из сферы с радиусом .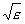

Отметим некоторые особенности определения устойчивости по А. М. Ляпунову. Во-первых, предполагают, что возмущения налагаются только на начальные условия, иначе говоря, возмущенное движение происходит при тех же силах (источниках энергии), что и невозмущенное движение. Во-вторых, устойчивость рассматривают на бесконечно большом промежутке времени. В-третьих, возмущения предполагаются малыми.