Распространение света в оптическом волокне

· Относительная разность показателей преломления:

(7.1)

где - показатель преломления сердцевины волокна, - показатель преломления оболочки.

· Числовая апертура NA связана с максимальным углом вводимого в волокно излучения из свободного пространства, при котором световой луч испытывает полное отражение и распространяется в волокне :

(7.2)

Для волокна со ступенчатым показателем преломления числовая апертура:

(7.3)

Для градиентного волокна локальная числовая апертура зависит от r-расстояния от оси волокна:

(7.4)

· Нормированная частота V:

(7.5)

где d - диаметр сердцевины волокна.

· Количество мод, распространяющихся в волокне. В волокне распространяется только одна мода при выполнении условия :

.

· Количество мод, распространяющихся в волокне при больших значениях параметра V.

а) для волокна со ступенчатым профилем показателя преломления:

(7.6)

б) для волокна с произвольным профилем показателя преломления , где а- радиус сердцевины, a - некоторый параметр:

(7.7)

· Длина волны отсечки (волоконная длина волны отсечки) - минимальная длина волны, при которой волокно поддерживает только одну распространяемую моду:

(7.8)

· Дисперсия- уширение импульсов - определяется как квадратичная разность длительностей импульсов на выходе и входе кабеля длины L [3] : и имеет размерность времени.

Обычно дисперсия нормируется в расчете на 1 км, и измеряется в пс/км:

. (7.9)

Дисперсия в общем случае характеризуется тремя основными факторами, рассматриваемыми ниже:

ü различием скоростей распространения направляемых мод (межмодовой дисперсией t_mod),

ü направляющими свойствами световодной структуры (волноводной дисперсией t_w),

ü свойствами материала оптического волокна (материальной дисперсией t_mat).

Волноводная и материальная дисперсии вместе составляют хроматическую дисперсию t_chr.

В некоторых случаях необходимо учитывать также поляризационную дисперсию t_pmd.

Результирующая дисперсия t определяется из формулы

. (7.10)

· Межмодовая дисперсия и полоса пропускания

Межмодовая дисперсия возникает вследствие различной скорости распространения у мод, и имеет место только в многомодовом волокне. Для ступенчатого многомодового волокна ее можно вычислить соответственно по формуле:

, (7.11)

для градиентного многомодового волокна с параболическим профилем показателя преломления по формуле:

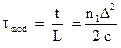, (7.12)

где n₁ - показатель преломления сердцевины, ,

n₂ - показатель преломления оболочки.

Формулы (3) и (4) справедливы при длине волокна 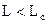, где L_c- длина межмодовой связи. (для ступенчатого волокна порядка 5 км, для градиентного - порядка 10 км. Обычно длины линий связи между активными устройствами при использовании многомодового волокна не превосходят 2 км и значительно меньше длины межмодовой связи. Поэтому можно пользоваться вышеприведенными формулами.

· Полоса пропусканияхарактеризует способность волокна передавать определенные объемы информации в единицу времени. Чем шире полоса, тем выше информационная емкость волокна. При расчете полосы пропускания W можно пользоваться формулой:

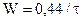. (7.13)

Полоса пропускания измеряется в МГц×км.

· Физический смысл полосы пропускания W - это максимальная частота модуляции передаваемого сигнала при длине линии 1 км. Если дисперсия линейно растет с ростом расстояния, то полоса пропускания обратно пропорционально зависит от расстояния.

· Хроматическая дисперсия

Хроматическая дисперсия состоит из материальной и волноводной составляющих и имеет место при распространении как в одномодовом, так и в многомодовом волокне. Однако наиболее отчетливо она проявляется в одномодовом волокне, в виду отсутствия межмодовой дисперсии.

· Материальная дисперсия обусловлена зависимостью показателя преломления волокна от длины волны. В выражение для дисперсии одномодового волокна входит дифференциальная зависимость показателя преломления от длины волны:

. (7.14)

Зависимость параметра от длины волны для объемного образца для чистого кварца приведена на рисунке 7.1., параметры источников излучения даны в таблице 7.1.

· Волноводная дисперсия обусловлена зависимостью коэффициента распространения моды от длины волны:

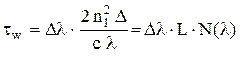, (7.15)

где коэффициенты M(l) и N(l) - удельные материальная и волноводная дисперсии соответственно, а Dl(нм) - спектральная ширина источника излучения.

Хроматическую дисперсию (с учетом материальной и волноводной дисперсии) можно найти по следующей формуле:

, (7.16)

где - результирующий коэффициент удельной хроматической дисперсии. измеряется в .

При определенной длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) хроматическая дисперсия ( а следовательно и коэффициент D(l)) обращается в нуль. Длина волны, при которой это происходит, называется длиной волны нулевой дисперсии l_о. Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться l_о для данного конкретного волокна.

Для одномодового ступенчатого и многомодового градиентного волокна используется для аппроксимации эмпирическая формула Селмейера (Sellmeier, [2]):

.

Коэффициенты A, B, C являются подгоночными, и выбираются так, чтобы экспериментальные точки лучше ложились на . Тогда удельная хроматическая дисперсия вычисляется по формуле:

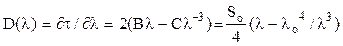, (7.17)

где l_о - длина волны нулевой дисперсии ,

новый параметр S_о - наклон нулевой дисперсии ( его размерность пс/(нм²*км)),

l - рабочая длина волны, для которой определяется удельная хроматическая дисперсия.

Для волокна со смещенной дисперсией эмпирическая формула временных задержек записывается в виде:

,

а соответствующая удельная дисперсия определяется как:

(7.18)

где l_о - длина волны нулевой дисперсии,

S_о - наклон нулевой дисперсии,

l - рабочая длина волны, для которой определяется удельная хроматическая дисперсия.

К уменьшению хроматической дисперсии ведет использование более когерентных источников излучения, например лазерных передатчиков, и использование рабочей длины волны более близкой к длине волны нулевой дисперсии.