ПОВЕРХНОСТЬ ПИРАМИДЫ И УСЕЧЕННОЙ ПИРАМИДЫ

Определение: Площадью полной поверхности пирамиды (усечённой пирамиды) называется сумма площадей всех её граней.

Определение: Площадью боковой поверхности пирамиды (усечённой пирамиды) называется сумма площадей её боковых граней.

Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра её основания на апофему.

Дано:

SABC – правильная пирамида; ;

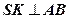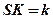; – апофема;

.

Доказать: .

Теорема: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему.

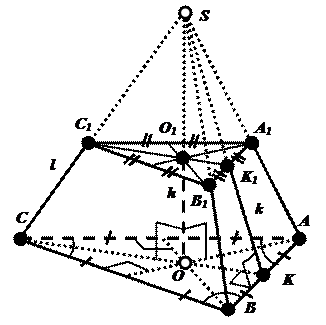Дано:

– правильная усечённая пирамида;

; ;

; ;

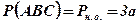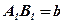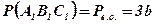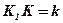– апофема;

Доказать:

.

Пример: В основании пирамиды лежит равнобедренный прямоугольный треугольник, катеты которого равны а. Боковые рёбра пирамиды наклонены к основанию под углом 60°. Найти площадь полной поверхности пирамиды.

Дано:

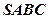- пирамида;

; ; ;

;

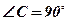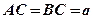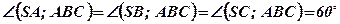Определить: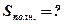

Решение:

; ; ; ;

; ; .

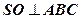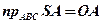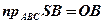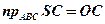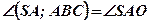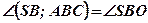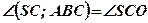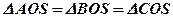по стороне и прилежащим к ней углам:

1) SO - общая сторона;

2) , так как , , ;

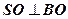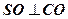3) .

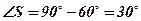Из равенства треугольников следует, что и .

Точка О одинаково удалена от вершин треугольника АВС, следовательно, она является центром окружности, описанной около этого треугольника. Центр окружности, описанной около прямоугольного треугольника, есть середина гипотенузы. Точка О - середина гипотенузы.

.

; .

; ; ; ; .

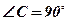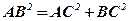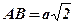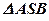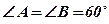; , следовательно, .

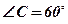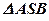- равносторонний треугольник, значит, .

; .

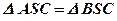по трём сторонам, следовательно, .

;

; ;

;

.

.

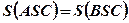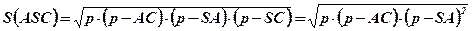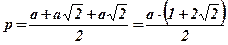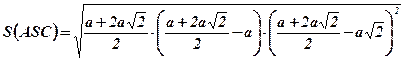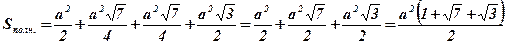Ответ: .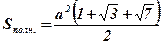

Замечание: Площадь боковой поверхности неправильнойусечённой пирамиды вычисляется по определению, каксумма площадей её боковых граней.

Упражнения:

1. Найти площадь полной поверхности пирамиды, основанием которой служит ромб с диагоналями 12 см и 16 см, а высота проходит через точку пересечения диагоналей ромба и равна 6,4 см.
2. Основанием пирамиды SABC является прямоугольный треугольник АВС с гипотенузой АВ = 25 см и катетом ВC = 7 см. Ребро SA перпендикулярно основанию и равно 18 см. Найти площадь полной поверхности пирамиды.
3. Найти площадь боковой поверхности правильной шестиугольной пирамиды, высота которой равна 4 дм, а боковое ребро равно 16 дм.
4. Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 18 см и 8 см, а высота равна 12 см.
5. Площадь боковой поверхности правильной четырёхугольной усечённой пирамиды вдвое меньше площади её полной поверхности. Стороны её оснований равны 12 дм и 6 дм. Найти высоту усечённой пирамиды.
6. Сторона нижнего основания правильной треугольной усечённой пирамиды равна 4 дм. Боковое ребро наклонено к плоскости основания под углом 60°. Найти площадь боковой поверхности усечённой пирамиды, если её высота равна 1 дм.
7. Площадь полной поверхности правильной четырёхугольной пирамиды равна 108 см². Двугранный угол при основании пирамиды равен 60°. Вычислить объём пирамиды.
8. Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 8 дм и 6 дм и боковая грань наклонена к большему основанию под углом 60°.

ОБЪЁМ ПИРАМИДЫ

Теорема: Объём пирамиды равен одной трети произведения площади основания пирамиды на её высоту.

Дано:

SABC - пирамида;

S(ABC)= S_осн.

SО ^ АВС; SО = h.

Доказать:

9. 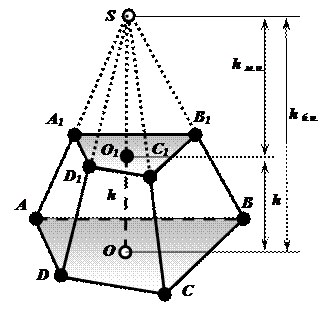ОБЪЁМ УСЕЧЕННОЙ ПИРАМИДЫ

Дано:

ABCDA₁B₁C₁D₁ - усечённая пирамида;

S(ABCD) = S_н.о.; S (A₁B₁C₁D₁) = S_в.о.

h - высота усечённой пирамиды;

Определить: V_ус.пир.- ?

.

Упражнения:

1. Диагональ квадратного основания правильной пирамиды равна 6 см, высота пирамиды равна 15 см. Найти её объём.
2. Боковое ребро правильной шестиугольной пирамиды равно 14 дм, сторона её основания равна 2 дм. Найти объём пирамиды.
3. Основанием пирамиды является ромб со стороной 15 см. Боковые грани пирамиды наклонены к плоскости основания под углом 45°. Большая диагональ основания равна 24 см. Найти объём пирамиды.
4. Найти объём усечённой пирамиды, если площади её оснований равны 98 см² и 32 см², а высота соответствующей полной пирамиды равна 14 см.
5. В пирамиде через середину высоты проведена плоскость, параллельная её основанию. Определить объём образовавшейся усечённой пирамиды, если высота данной пирамиды равна 18 см, а площадь её основания равна 400 см².
6. Найти объём треугольной пирамиды, боковые рёбра которой попарно перпендикулярны и равны 10 см, 15 см, 9 см.
7. В треугольной усечённой пирамиде высота равна 10 см, стороны нижнего основания равны 27 м, 29 м, 52 м, а периметр верхнего основания равен 72 м. Найти объём усечённой пирамиды.
8. Стороны оснований правильной четырёхугольной усечённой пирамиды равны 40 см и 10 см. Площадь её полной поверхности равна 3400 см². Найти объём усечённой пирамиды.

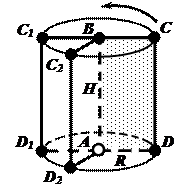ЦИЛИНДР. ПОВЕРХНОСТЬ И ОБЪЕМ ЦИЛИНДРА.

Определение: Геометрическое тело, полученное при вращении прямоугольника вокруг одной из его сторон, называется прямым круговым цилиндром.

Определение: Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

AB – ось симметрии, высота цилиндра;AB = H;

AD– радиус основания цилиндра;AD = R.

Определение: Расстояние между плоскостями оснований является высотой прямого кругового цилиндра.

Радиусом цилиндра называется радиус его основания. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Два круга являются основаниями прямого кругового цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный плоскостям оснований, называется образующей прямого кругового цилиндра.

Определение: Прямоугольник, одна сторона которого равна длине окружности основания цилиндра, а другая – его высоте, называется разверткой боковой поверхности цилиндра.

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.

Определение: Цилиндр называется равносторонним, если его высота равна диаметру основания.

 

Сечения цилиндра.

Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник. Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.

В частности, прямоугольником является осевое сечение. Осевое сечение - сечение цилиндра плоскостью, проходящей через его ось.

Сечение цилиндра плоскостью, параллельной основанию − круг.

Сечение цилиндра плоскостью не параллельной основанию и его оси – овал.

 

Теорема: Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (S_бок. = 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).

Определение: Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.

S_осн. = πR² S_бок. = 2πRH S_полн.= 2πRH + 2πR².

 

Рассмотрим п-угольную прямую призму. При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра.

Определение: Призма называется вписанной в цилиндр, если её основания вписаны в основания цилиндра.

Определение: Цилиндр называется вписанным в призму, если его основания вписаны в основания призмы.

Упражнения:

1. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60°. Найти: высоту, радиус основания, площадь основания цилиндра.

2. Площадь осевого сечения цилиндра равна 10 см², а площадь основания - 5 см². Найти высоту цилиндра.

3. Радиус основания цилиндра равен 4 см, а площадь его осевого сечения равна 72 см². Найти объём цилиндра.

Стальная болванка имеет форму правильной четырёхугольной призмы со стороной основания о,40 м и высотой 1,00 м. Сколько метров проволоки можно изготовить из этой болванки вытягиванием?