Построение 12 положений механизма в масштабе

Структурный анализ

Кривошипно – ползунный механизм

0 – стойка

1 – кривошип

2 – шатун

3 – ползун

4 – шатун

Обозначение пары	Подвижность пары	Звенья, образующие пару	Какая пара
А10	Одноподвижная	Стойка – кривошип	Низшая, вращательная
В12	Одноподвижная	Кривошип – шатун	Низшая, вращательная
С23	Одноподвижная	Шатун – ползун	Низшая, вращательная
C30	Одноподвижная	Ползун - стойка	Низшая, поступательная
D14	Одноподвижная	Кривошип – шатун	Низшая, вращательная
E45	Одноподвижная	Шатун – ползун	Низшая, вращательная
E50	Одноподвижная	Ползун - стойка	Низшая, поступательная

5 – ползун

Определим степень свободы механизма по формуле Чебышева П.Л. для плоских механизмов:

 

W = 3n – 2p₁ – p₂= 3×5 – 2×7 = 15 – 14 = 1

 

где n – число подвижных звеньев

p₁ – число одноподвижных кинематических пар

p₂ – число двух подвижных кинематических пар

 

Построение 12 положений механизма в масштабе

Изм.

Лист

№ докум.

Дата

Лист

Исходные данные:

Радиус кривошипа r_AB=r_AD= 0.125 м

Длины шатунов l_BC = l_DE=0.5м

Кривошип AB =AD= 30 мм

1. Рассчитаем масштабный коэффициент: μ_l = = 0.00416м/мм ;

2. Длины шатунов на чертеже:

 

3. Строим 12 положений кривошипно – ползунного механизма ;

4. Соответствующие положения остальных звеньев находим методом засечек;

5. Соединяем точки C₁₀, B_10,D₁₀ и получим положения звеньев.

1.3. Построение планов скоростей

Изм.

Лист

№ докум.

Подпись

Дата

Лист

Дано n_AB = 650об/мин

1. Определим скорость точки B кривошипа;

_B=ω₁×r_AB

ω₁ = const = 68.03 c^-1

_B= 68.03 0.125=7.3 м/с

2. Для построения плана скоростей выберем на плоскости произвольную точку

p – полюс плана скоростей. Отложим из полюса скорость точки В в виде вектора произвольной длины, т.к. траектория точки В окружность, то её скорость направлена по касательной к траектории или перпендикулярна радиусу АВ;

3. Рассчитаем масштабный коэффициент плана скоростей;

4. Рассмотрим первую группу звеньев (звенья 2 и 3). Для того что бы найти скорость точки С, которая одновременно принадлежит и шатуну и ползуну, графически решим систему уравнений;

Так как план скоростей полярный, то все абсолютные скорости точек направлены из полюса.

5. Чтобы определить истинную величину любого из векторов в м/с, надо его длину умножить на масштаб плана скоростей;

м/с

м/с

6. Рассчитаем скорости второй группы (4 и 5 звенья):

 

7. Скорости точек S₂ и S₄ находим по теореме подобия

Теорема: Одноименные фигуры на плане механизма и на плане скорости подобны, а их сходственные стороны взаимно перпендикулярны.

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1.4. Построение планов ускорения

1. Определяем ускорение токи B

м/с²;

2. Для построения плана ускорений выбираем на плоскости произвольную точку

π – полюс плана ускорений. Отложим из него ускорение точки В в виде вектора произвольной длины, направление ускорения точки В к центру вращения, то есть к точке А (|| AB);

3. Рассчитаем масштабный коэффициент плана ускорения;

3. Рассчитаем масштабный коэффициент плана ускорения;

4. Чтобы найти ускорение точки в 10 положении С составим систему уравнений:

На плане ускорений

5. Чтобы найти ускорение точки Е составим систему уравнений:

6. Строим план ускорений для 10 положения:

На плане ускорений

7.Аналогично построим план ускорений для нулевого положения механизма;

На плане ускорений

 

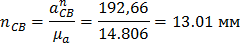
На плане ускорений

8. Скорости точек S₂ и S₄ находим по теореме подобия

Теорема: Одноименные фигуры на плане механизма и на плане скорости подобны, а их сходственные стороны взаимно перпендикулярны.

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1.5. Построение кинематических диаграмм ползуна

1. φ – угол поворота кривошипа;

2. Перемещение ползуна от 0 положения до С₁, С₂, С₃ … - ординаты графика S_c–φ;

3. Т.к. перемещение ползуна откладываем без искажения, то µ_s=µ_l= 0,0067м/мм;

4.График скорости получим из графика перемещения, методом графического дифференцирования.

Для этого:

1.Проводим хорду на участке 01;

2.Влево от начала координат 2 графика отводим полюсное расстояние Н₁ = 10 мм;

3.Из полюса Р второго графика построим луч параллельный первой хорде до оси ординат;

4.Полученную точку на оси ординат переносим на середину участка 01 второго графика;

5. Аналогично поступаем с хордами 12,23 и.т.д.

6.Вычислим масштабный коэффициент скорости:

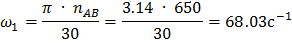
5.Аналогичным способом получим кривую ускорения, дифференцируя график скорости (Н₂=30 мм);

Масштаб определим по формуле:

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

1.6. Сравнительный анализ

 

Сводная таблица скоростей

 

N кол
м/с		3.44	6.63	9.28	7.36	4.51	1.85	3.44	6.63	9.28	7.69	4.51	1.85

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист