Пузырьковая сортировка

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n2)	O(n2)
Память	O(1)	O(1)	O(1)

Сортировка пузырьком — это самый простой алгоритм сортировки. Он проходит по массиву несколько раз, на каждом этапе перемещая самое большое значение из неотсортированных в конец массива.

Например, у нас есть массив целых чисел:

При первом проходе по массиву мы сравниваем значения 3 и 7. Поскольку 7 больше 3, мы оставляем их как есть. После чего сравниваем 7 и 4. 4 меньше 7, поэтому мы меняем их местами, перемещая семерку на одну позицию ближе к концу массива. Теперь он выглядит так:

Этот процесс повторяется до тех пор, пока семерка не дойдет почти до конца массива. В конце она сравнивается с элементом 8, которое больше, а значит, обмена не происходит. После того, как мы обошли массив один раз, он выглядит так:

Поскольку был совершен по крайней мере один обмен значений, нам нужно пройти по массиву еще раз. В результате этого прохода мы перемещаем на место число 6.

И снова был произведен как минимум один обмен, а значит, проходим по массиву еще раз.

При следующем проходе обмена не производится, что означает, что наш массив отсортирован, и алгоритм закончил свою работу.

public void Sort(T[] items){bool swapped; do{swapped=false;for(int i =1; i <items.Length; i++){if(items[i -1].CompareTo(items[i])>0){Swap(items, i -1, i);swapped=true;}}}while(swapped!=false);}

Сортировка вставками

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n2)	O(n2)
Память	O(1)	O(1)	O(1)

Сортировка вставками работает, проходя по массиву и перемещая нужное значение в начало массива. После того, как обработана очередная позиция, мы знаем, что все позиции до нее отсортированы, а после нее — нет.

Важный момент: сортировка вставками обрабатывает элементы массива по порядку. Поскольку алгоритм проходит по элементам слева направо, мы знаем, что все, что слева от текущего индекса — уже отсортировано. На этом рисунке показано, как увеличивается отсортированная часть массива с каждым проходом:

Постепенно отсортированная часть массива растет, и, в конце концов, массив окажется упорядоченным.

Давайте взглянем на конкретный пример. Вот наш неотсортированный массив, который мы будем использовать:

Алгоритм начинает работу с индекса 0 и значения 3. Поскольку это первый индекс, массив до него включительно считается отсортированным.

Далее мы переходим к числу 7. Поскольку 7 больше, чем любое значение в отсортированной части, мы переходим к следующему элементу.

На этом этапе элементы с индексами 0..1 отсортированы, а про элементы с индексами 2..n ничего не известно.

Следующим проверяется значение 4. Так как оно меньше семи, мы должны перенести его на правильную позицию в отсортированную часть массива. Остается вопрос: как ее определить? Это осуществляется методом FindInsertionIndex. Он сравнивает переданное ему значение (4) с каждым значением в отсортированной части, пока не найдет место для вставки.

Итак, мы нашли индекс 1 (между значениями 3 и 7). Метод Insert осуществляет вставку, удаляя вставляемое значение из массива и сдвигая все значения, начиная с индекса для вставки, вправо. Теперь массив выглядит так:

Теперь часть массива, начиная от нулевого элемента и заканчивая элементом с индексом 2, отсортирована. Следующий проход начинается с индекса 3 и значения 4. По мере работы алгоритма мы продолжаем делать такие вставки.

Когда больше нет возможностей для вставок, массив считается полностью отсортированным, и работа алгоритма закончена.

public void Sort(T[] items){intsortedRangeEndIndex=1; while(sortedRangeEndIndex<items.Length){if(items[sortedRangeEndIndex].CompareTo(items[sortedRangeEndIndex-1])<0){intinsertIndex=FindInsertionIndex(items, items[sortedRangeEndIndex]);Insert(items,insertIndex,sortedRangeEndIndex);} sortedRangeEndIndex++;}} privateintFindInsertionIndex(T[] items, T valueToInsert){for(int index =0; index <items.Length; index++){if(items[index].CompareTo(valueToInsert)>0){return index;}} thrownewInvalidOperationException("The insertion index was not found");} private void Insert(T[]itemArray,intindexInsertingAt,intindexInsertingFrom){// itemArray = 0 1 2 4 5 6 3 7// insertingAt = 3// insertingFrom = 6// // Действия:// 1: Сохранитьтекущийиндексв temp// 2: ЗаменитьindexInsertingAtнаindexInsertingFrom// 3: ЗаменитьindexInsertingAtнаindexInsertingFromвпозиции +1// Сдвинуть элементы влево на один.// 4: Записать temp на позицию в массиве + 1. // Шаг 1. T temp =itemArray[indexInsertingAt]; // Шаг 2. itemArray[indexInsertingAt]=itemArray[indexInsertingFrom]; // Шаг 3.for(int current =indexInsertingFrom; current >indexInsertingAt; current--){itemArray[current]=itemArray[current -1];} // Шаг 4.itemArray[indexInsertingAt+1]=temp;}

Сортировка выбором

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n)	O(n2)	O(n2)
Память	O(1)	O(1)	O(1)

Сортировка выбором — это некий гибрид между пузырьковой и сортировкой вставками. Как и сортировка пузырьком, этот алгоритм проходит по массиву раз за разом, перемещая одно значение на правильную позицию. Однако, в отличие от пузырьковой сортировки, он выбирает наименьшее неотсортированное значение вместо наибольшего. Как и при сортировке вставками, упорядоченная часть массива расположена в начале, в то время как в пузырьковой сортировке она находится в конце.

Давайте посмотрим на работу сортировки выбором на нашем неотсортированном массиве.

При первом проходе алгоритм с помощью метода FindIndexOfSmallestFromIndex пытается найти наименьшее значение в массиве и переместить его в начало.

Имея такой маленький массив, мы сразу можем сказать, что наименьшее значение — 3, и оно уже находится на правильной позиции. На этом этапе мы знаем, что на первой позиции в массиве (индекс 0) находится самое маленькое значение, следовательно, начало массива уже отсортировано. Поэтому мы начинаем второй проход — на этот раз по индексам от 1 до n — 1.

На втором проходе мы определяем, что наименьшее значение — 4. Мы меняем его местами со вторым элементом, семеркой, после чего 4 встает на свою правильную позицию.

Теперь неотсортированная часть массива начинается с индекса 2. Она растет на один элемент при каждом проходе алгоритма. Если на каком-либо проходе мы не сделали ни одного обмена, это означает, что массив отсортирован.

После еще двух проходов алгоритм завершает свою работу:

public void Sort(T[] items){intsortedRangeEnd=0; while(sortedRangeEnd<items.Length){intnextIndex=FindIndexOfSmallestFromIndex(items,sortedRangeEnd);Swap(items,sortedRangeEnd,nextIndex); sortedRangeEnd++;}} privateintFindIndexOfSmallestFromIndex(T[] items,intsortedRangeEnd){ T currentSmallest=items[sortedRangeEnd];intcurrentSmallestIndex=sortedRangeEnd; for(int i =sortedRangeEnd+1; i <items.Length; i++){if(currentSmallest.CompareTo(items[i])>0){currentSmallest= items[i];currentSmallestIndex= i;}} returncurrentSmallestIndex;}

Сортировка слиянием

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n·log n)	O(n·log n)	O(n·log n)
Память	O(n)	O(n)	O(n)

 

Разделяй и властвуй

До сих пор мы рассматривали линейные алгоритмы. Они используют мало дополнительной памяти, но имеют квадратичную сложность. На примере сортировки слиянием мы посмотрим на алгоритм типа «разделяй и властвуй» (divideandconquer).

Алгоритмы этого типа работают, разделяя крупную задачу на более мелкие, решаемые проще. Мы пользуемся ими каждый день. К примеру, поиск в телефонной книге — один из примеров такого алгоритма.

Если вы хотите найти человека по фамилии Петров, вы не станете искать, начиная с буквы А и переворачивая по одной странице. Вы, скорее всего, откроете книгу где-то посередине. Если попадете на букву Т, перелистнете несколько страниц назад, возможно, слишком много — до буквы О. Тогда вы пойдете вперед. Таким образом, перелистывая туда и обратно все меньшее количество страниц, вы, в конце концов, найдете нужную.

Насколько эффективны эти алгоритмы?

Предположим, что в телефонной книге 1000 страниц. Если вы открываете ее на середине, вы отбрасываете 500 страниц, в которых нет искомого человека. Если вы не попали на нужную страницу, вы выбираете правую или левую сторону и снова оставляете половину доступных вариантов. Теперь вам надо просмотреть 250 страниц. Таким образом мы делим нашу задачу пополам снова и снова и можем найти человека в телефонной книге всего за 10 просмотров. Это составляет 1% от всего количества страниц, которые нам пришлось бы просмотреть при линейном поиске.

Сортировка слиянием

При сортировке слиянием мы разделяем массив пополам до тех пор, пока каждый участок не станет длиной в один элемент. Затем эти участки возвращаются на место (сливаются) в правильном порядке.

Давайте посмотрим на такой массив:

Разделим его пополам:

И будем делить каждую часть пополам, пока не останутся части с одним элементом:

Теперь, когда мы разделили массив на максимально короткие участки, мы сливаем их в правильном порядке.

Сначала мы получаем группы по два отсортированных элемента, потом «собираем» их в группы по четыре элемента и в конце собираем все вместе в отсортированный массив.

Для работы алгоритма мы должны реализовать следующие операции:

1. Операцию для рекурсивного разделения массива на группы (метод Sort).

2. Слияние в правильном порядке (метод Merge).

Стоит отметить, что в отличие от линейных алгоритмов сортировки, сортировка слиянием будет делить и склеивать массив вне зависимости от того, был он отсортирован изначально или нет. Поэтому, несмотря на то, что в худшем случае он отработает быстрее, чем линейный, в лучшем случае его производительность будет ниже, чем у линейного. Поэтому сортировка слиянием — не самое лучшее решение, когда надо отсортировать частично упорядченный массив.

public void Sort(T[] items){if(items.Length<=1){return;} intleftSize=items.Length/2;intrightSize=items.Length-leftSize;T[] left =newT[leftSize];T[] right =newT[rightSize];Array.Copy(items,0, left,0,leftSize);Array.Copy(items,leftSize, right,0,rightSize);Sort(left);Sort(right);Merge(items, left, right);} private void Merge(T[] items, T[] left, T[] right){intleftIndex=0;intrightIndex=0;inttargetIndex=0;int remaining =left.Length+right.Length;while(remaining >0){if(leftIndex>=left.Length){items[targetIndex]= right[rightIndex++];}elseif(rightIndex>=right.Length){items[targetIndex]= left[leftIndex++];}elseif(left[leftIndex].CompareTo(right[rightIndex])<0){items[targetIndex]= left[leftIndex++];}else{items[targetIndex]=right[rightIndex++];} targetIndex++;remaining--;}}

Быстрая сортировка

Сложность	Наилучший случай	В среднем	Наихудший случай
Время	O(n·log n)	O(n·log n)	O(n2)
Память	O(1)	O(1)	O(1)

 

Быстрая сортировка — это еще один алгоритм типа «разделяй и властвуй». Он работает, рекурсивно повторяя следующие шаги:

1. Выбрать ключевой индекс и разделить по нему массив на две части. Это можно делать разными способами, но в данной статье мы используем случайное число.

2. Переместить все элементы больше ключевого в правую часть массива, а все элементы меньше ключевого — в левую. Теперь ключевой элемент находится в правильной позиции — он больше любого элемента слева и меньше любого элемента справа.

3. Повторяем первые два шага, пока массив не будет полностью отсортирован.

Давайте посмотрим на работу алгоритма на следующем массиве:

Сначала мы случайным образом выбираем ключевой элемент:

intpivotIndex = _pivotRng.Next(left, right);

Теперь, когда мы знаем ключевой индекс (4), мы берем значение, находящееся по этому индексу (6), и переносим значения в массиве так, чтобы все числа больше или равные ключевому были в правой части, а все числа меньше ключевого — в левой. Обратите внимание, что в процессе переноса значений индекс ключевого элемента может измениться (мы увидим это вскоре).

Перемещение значений осуществляется методом partition.

На этом этапе мы знаем, что значение 6 находится на правильной позиции. Теперь мы повторяем этот процесс для правой и левой частей массива.

Мы рекурсивно вызываем метод quicksort на каждой из частей. Ключевым элементом в левой части становится пятерка. При перемещении значений она изменит свой индекс. Главное — помнить, что нам важно именно ключевое значение, а не его индекс.

Снова применяем быструю сортировку:

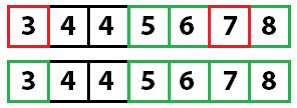
И еще раз:

У нас осталось одно неотсортированное значение, а, поскольку мы знаем, что все остальное уже отсортировано, алгоритм завершает работу.

Random _pivotRng=newRandom(); public void Sort(T[] items){quicksort(items,0,items.Length-1);} private void quicksort(T[] items,int left,int right){if(left < right){intpivotIndex= _pivotRng.Next(left, right);intnewPivot=partition(items, left, right,pivotIndex); quicksort(items, left,newPivot-1);quicksort(items,newPivot+1, right);}} privateintpartition(T[] items,int left,int right,intpivotIndex){ T pivotValue=items[pivotIndex]; Swap(items,pivotIndex, right); intstoreIndex= left; for(int i = left; i < right; i++){if(items[i].CompareTo(pivotValue)<0){Swap(items, i,storeIndex);storeIndex+=1;}} Swap(items,storeIndex, right);returnstoreIndex;}

Заключение

На этом мы заканчиваем наш цикл статей по алгоритмам и структурам данных для начинающих. За это время мы рассмотрели связные списки, динамические массивы, двоичное дерево поиска и множества с примерами кода на C#.