Программа базового уровня

2018-06-29

368

Обсуждений (0)

0.00 из 5.00 0 оценок

12 Следующая ⇒

Программа аттестации модуля 2

Содержание	Планируемые результаты обучения
Знания и представления	Умения и навыки
Модуль 2. Теория графов
Тема 2.1. Первичные понятия теории графов
Определение графа, классификация его элементов	Знать определение графа, представление графа диаграммой, классификацию ребер (кратные ребра, петли), определение обыкновенного графа, определения смежных вершин, инцидентных вершин и ребер, степени вершины, классификацию вершин (висячие, изолированные), утверждение о связи между суммой степеней вершин графа и числом его ребер (лемма о рукопожатиях).	Уметь задавать граф списком вершин и ребер, диаграммой, классифицировать его элементы.
Изоморфизм графов	Иметь представление о понятии изоморфных графов, о свойствах отношения изоморфизма графов.	Уметь иллюстрировать на примерах понятия изоморфных и неизоморфных графов.
Специальные виды графов	Знать специальные виды графов (полные, двудольные, полные двудольные, одноэлементные, нулевые).	Уметь определять принадлежность графа к тому или иному специальному виду.
Задание графа матрицами	Знать определения матриц смежности и инцидентности и их свойства.	Уметь строить матрицу смежности и инцидентности графа, заданного списком вершин и ребер или диаграммой, и задавать граф матрицей смежности или инцидентности.
Подграфы	Знать определение подграфа, подграфа, порожденного подмножеством вершин, остовного подграфа.	Уметь иллюстрировать понятия, относящиеся к подграфам на примерах.
Операции над графами	Знать определения операций над графами (объединение, пересечение, декартово произведение, удаление вершин, ребер), определение дизъюнктного разбиения графа.	Уметь иллюстрировать операции над графами на примерах.
Тема 2.2. Достижимость и компоненты связности, циклы и мосты, цикломатическое число
Пути, цепи, циклы на графе.	Знать определения пути, цепи, простой цепи. цикла, простого цикла на графе.	Уметь строить пути, цепи, простые циклы, цепи, простые цепи на графе.
Отношение достижимости (связности), компоненты связности графа.	Знать определение отношения достижимости (связности) на множестве вершин графа, свойства этого отношения, определения компонент связности графа и числа связности, определение связного графа.	Уметь находить компоненты связности графа, определять число связности.
Мосты графа, связь между мостами и циклами.	Знать определение моста графа, формулировки теоремы о мостах, теоремы о мостах и циклах.
Цикломатическое число графа	Знать определение цикломатического числа графа, формулировку теоремы о знаке цикломатического числа.	Уметь находить цикломатическое число графа.
Тема 2.3. Деревья и леса
Дерево, лес, их характеристические свойства	Знать определения дерева и леса, характеристические свойства деревьев и лесов.	Уметь иллюстрировать понятия дерева и леса на примерах.
Остовы графа	Знать определение остова графа, понятие матрицы Кирхгофа и свойства этой матрицы, алгоритм отыскание числа остовов графа с помощью матрицы Кирхгофа.	Уметь находить остовы связного графа, число остовов обыкновенного связного графа по его матрице Кирхгофа.
Алгоритм Краскала отыскания минимального остова	Знать понятия взвешенного графа, минимального остова взвешенного графа, алгоритм Краскала отыскания минимального остова.	Уметь строить остов минимального веса с помощью алгоритма Краскала.
Кодирование деревьев	Знать определения бинарного кода корневого дерева, кода из натуральных чисел (Прюфера), алгоритмы кодирования и декодирования деревьев	Уметь строить бинарный код корневого дерева, код Прюфера дерева с занумерованными вершинами, восстанавливать по этим кодам деревья (изображать их диаграммы).
Тема 2.4. Планарность
Укладки графов в трехмерном пространстве	Знать определение укладки графа в трехмерном пространстве и доказательство ее существования для любого графа.
Укладка графа на плоскости. Планарные графы. Формула Эйлера.	Знать определение укладки графа на плоскости, понятия планарного графа, плоского графа, граней плоского графа, формулу Эйлера для связных плоских графов, доказательство непланарности графов и 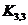.	Уметь приводить примеры планарных и непланарных графов.
Тема 2.5. Обходы графов
Эйлеровы цикл и цепь, критерии их существования.	Знать определение эйлерова цикла и цепи, критерии существования эйлерового цикла и эйлеровой цепи на графе.	Уметь иллюстрировать на примерах понятия эйлерова цикла и эйлеровой цепи, по набору степеней вершин графа определять, существует ли на связном графе эйлеровы цикл и цепь.
Алгоритм Флери построения эйлерового цикла (цепи).	Знать алгоритм Флери построения эйлерового цикла.	Уметь строить эйлеров цикл (цепь), используя алгоритм Флери.
Гамильтоновы цикл и цепь	Знать определения гамильтонова цикла и гамильтоновой цепи.	Уметь иллюстрировать на примерах понятия гамильтонового цикла и гамильтоновой цепи.
Тема 2.6. Раскраска графа
Раскраска графа. Хроматическое число графа.	Знать определение раскраски графа в цветов, -хроматического графа, хроматического числа графа.	Уметь определять хроматическое число графа и раскрашивать в равное этому числу количество красок графы с небольшим количеством вершин и ребер.
Критерий бихроматичности	Знать необходимые и достаточные условия бихроматичности.
Тема 2.7. Ориентированные графы
Ориентированный граф (орграф) и его элементов.	Знать определение ориентированного графа (орграфа), его диаграммы, полустепени исхода (захода) вершины, классификацию вершин и дуг, утверждение о связи между суммой полустепеней вершин графа и числом его дуг, определение основания орграфа.	Уметь задавать орграф списком вершин и дуг, диаграммой, классифицировать его элементы.
Изоморфные орграфы	Знать определение изоморфных орграфов.	Уметь иллюстрировать понятие изоморфизма на примерах.
Матрицы смежности и инцидентности орграфа	Знать определение матриц смежности и инцидентности орграфа.	Уметь строить матрицу смежности и инцидентности орграфа, заданного списком вершин и дуг или диаграммой, задавать орграф матрицей смежности или инцидентности.
Пути, цепи, циклы на орграфе. Слабая и сильная связность орграфа.	Знать определение пути, цепи, цикла, контура на орграфе, отношения достижимости на множестве вершин орграфа, определение слабой и сильной связности орграфа.	Уметь находить пути, цепи, простые циклы, цепи, простые цепи на графе, иллюстрировать на примерах понятия слабой (сильной) связности.
Понятие ориентированного дерева.	Иметь представление о понятии ориентированного дерева, его элементах, о понятии бинарного дерева	Уметь приводить примеры ориентированных деревьев, бинарных деревьев.
Тема 2.8. Задача о максимальном потоке в сети
Потоки в сети, задача о максимальном потоке	Знать определение сети, потока в сети, понятие максимального потока, постановку задачи о максимальном потоке, определения разреза, пропускающей способности разреза, минимального разреза.	Уметь иллюстрировать понятия, относящиеся к потокам и разрезам в сети на примерах.
Алгоритм Форда-Фалкерсона построения максимального потока	Знать алгоритм Форда-Фалкерсона построения максимального потока, процедуру отыскания минимального разреза.	Уметь строить максимальный поток и минимальный разрез в сети.
Тема 2.9. Кратчайшие пути на графе
Постановка задачи об отыскании кратчайших путей в сети	Знать определения длины пути, расстояния между вершинами, постановку задачи отыскания кратчайших путей в сети.	Уметь иллюстрировать понятия, относящиеся к постановке задачи о кратчайших путях в сети, на примерах
Алгоритм Дейкстры.	Иметь представление об алгоритме Дейкстры.	Уметь находить расстояния и кратчайшие пути от выделенной вершины сети до остальных ее вершин, используя алгоритм Дейкстры.
Тема 2.10. Схемы из функциональных элементов
Схемы из функциональных элементов в базисе	Иметь представление о схемах из функциональных элементов в базисе , о классификации ее вершин (входы, выходы, функциональные элементы), о сложности схемы.	Уметь иллюстрировать понятия, относящиеся к схемам из функциональных элементов, на примерах.
Реализация булевых функций схемами из функциональных элементов.	Иметь представление о функции, реализуемой схемой.	Уметь определить функцию, реализуемую схемой, и построить схему, реализующую функцию, заданную формулой над .
Проблемы анализа и синтеза схем.	Иметь представление о проблемах анализа и синтеза схем.
Тема 2.11. Упорядоченная бинарная диаграмма решений
Понятие упорядоченных бинарных диаграмм решений (УБДР). Минимальные УБДР.	Иметь представление об упорядоченной бинарной диаграмме решений (УБДР), о минимальной УБДР.	Уметь иллюстрировать на примерах построение УБДР функции относительно заданного порядка переменных.
Сокращенные УБДР, их построение для функции, заданной таблично.	Иметь представление о правилах удаления и слияния вершин, о сокращенной УБДР, об алгоритме построения сокращенной УБДР из УБДР функции относительно заданного порядка переменных.	Уметь иллюстрировать на примерах построение сокращенной УБДР функции из УБДР функции относительно заданного порядка переменных.

2018-06-29

368

Обсуждений (0)

0.00 из 5.00 0 оценок

12 Следующая ⇒

Обсуждение в статье: Программа базового уровня

Обсуждений еще не было, будьте первым... ↓↓↓