 |
Главная |
Проверка гипотезы о равенстве средних (сравнение результатов измерений)
|
из
5.00
|
Пусть имеются две независимые выборки результатов наблюдений случайной величины Х объемом n1 иn2. Случайная величина Хподчиняется нормальному закону распределения. Будем считать выборки из разных генеральных совокупностей Х1иХ2одной и той же случайной величиной Х. Необходимо проверить нулевую гипотезу 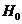 , состоящую в том, что
, состоящую в том, что 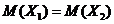 . Числовые значения дисперсий для генеральных совокупностей неизвестны, поэтому необходимо пользоваться их оценками. Вычислим сводную оценку дисперсии
. Числовые значения дисперсий для генеральных совокупностей неизвестны, поэтому необходимо пользоваться их оценками. Вычислим сводную оценку дисперсии
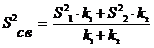 ,
, 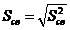 .
.
Если гипотеза 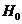 справедлива, то величина t
справедлива, то величина t
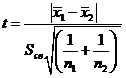
имеет распределение Стьюдента.
Определим 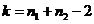 , причем в этом случае это значение будет соответствовать числу степеней свободы t – распределения.
, причем в этом случае это значение будет соответствовать числу степеней свободы t – распределения.
Если вычисленное значение 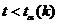 , то с вероятностью
, то с вероятностью 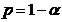 можно считать расхождение средних значений незначимым (случайным) и данные выборки можно объединить, т.е. нулевая гипотеза принимается.
можно считать расхождение средних значений незначимым (случайным) и данные выборки можно объединить, т.е. нулевая гипотеза принимается.
Если значение 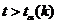 , то с вероятностью
, то с вероятностью 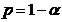 выдвинутая гипотеза о равенстве средних отвергается, видимо расхождение между средними значениями выборок неслучайно.
выдвинутая гипотеза о равенстве средних отвергается, видимо расхождение между средними значениями выборок неслучайно.
Проверка гипотез о законе распределения (критерий Пирсона)
Необходимо установить: какому закону распределения подчиняется случайная величина. Для проверки гипотезы воспользуемся экспериментальными результатами. Всю область значений случайной величины, представленной в выборке, следует разбить на l интервалов и подсчитать количество элементов выборки nj, попавших в каждый из интервалов Dj. Распределение частот значений nj по интервалам представляет собой эмпирическое распределение случайной величины.
В теоретическом распределении определяется вероятность pj попадания случайной величины Х в интервал Dj, используя то теоретическое распределение, о котором выдвинута гипотеза. Для выборки теоретическое число значений случайной величины Х попавших в интервал Dj, можно рассчитывать как npj.
Полученные значения представлены в виде таблицы:
| Интервалы | D1 | D2 | D3 | … | Dk |
| Эмпирические частоты | n1 | n2 | n3 | … | nk |
| Теоретические частоты | np1 | np2 | np3 | … | npk |
Здесь: 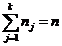 ,
, 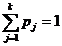 .
.
Степень расхождения между эмпирическими и теоретическими частотами оценивается по критерию согласия Пирсона: 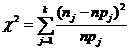 .
.
Критерий Пирсона имеет распределение c2-квадрат со степенями свободы 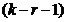 , где r – число параметров распределения F(X).
, где r – число параметров распределения F(X).
Рассчитав значение c2 и выбрав уровень значимости a, по таблице c2 - распределения определяют 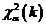 . Если
. Если 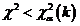 , то гипотезу H0 о законе распределения случайной величины принимают; если
, то гипотезу H0 о законе распределения случайной величины принимают; если 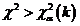 ,то гипотезу H0 отвергают.
,то гипотезу H0 отвергают.
Линейная корреляция
Основная задача корреляционного анализа – установление тесноты связи между случайными переменными (величинами).
Рассмотрим случай корреляции на примере двух случайных величин (Y, X). Связь между двумя случайными величинами можно выразить через корреляционный момент K или ковариацию: 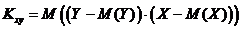 .
.
Корреляционный момент характеризует рассеяние и зависимость случайных величин. Если одна из составляющих величин незначительно отклоняется от своего математического ожидания, то корреляционный момент мал, как бы тесно не были связаны YиX.
Чтобы избежать влияния величины рассеяния на корреляционный момент, перейдем к безразмерной характеристике:
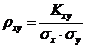 .
.
Эту безразмерную характеристику называют коэффициентом линейной корреляции случайных величин.
Для независимых случайных величин коэффициент корреляции и корреляционный момент равны нулю. Обратное утверждение – если коэффициент корреляции между двумя случайными величинами равен нулю, то эти две величины независимы – не всегда справедливо.
Поэтому вводится понятие коррелированности. Две случайные величины называются коррелированными, если коэффициент корреляции отличен от нуля. Если r= 0, то величины Yи Xнекоррелированы.
Таким образом, если случайные величины Yи X независимы, то они и некоррелированы.
Оценку теоретическому значению коэффициента линейной корреляции r обозначим как r:
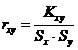 ,
,
где 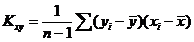 - несмещённая оценка ковариации,
- несмещённая оценка ковариации,
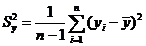 ,
, 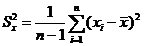 - оценки дисперсий.
- оценки дисперсий.
Пусть вычисленное значение 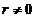 . Возникает вопрос, объясняется ли это действительно существующей линейной корреляционной связью между переменными XиY в генеральной совокупности или является следствием случайности отбора переменных в выборку (то есть придругом отборе возможно, например, r=0 или изменение знака r).
. Возникает вопрос, объясняется ли это действительно существующей линейной корреляционной связью между переменными XиY в генеральной совокупности или является следствием случайности отбора переменных в выборку (то есть придругом отборе возможно, например, r=0 или изменение знака r).
Выдвигают нуль – гипотезу H0: r= 0. Для проверки вычисляют статистику 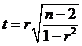 , которая подчиняется распределению Стьюдента с числом степеней свободы k = n – 2. По таблице определяют значение t -критерия для выбранного значения a (уровня значимости) и числа степеней свободы k.
, которая подчиняется распределению Стьюдента с числом степеней свободы k = n – 2. По таблице определяют значение t -критерия для выбранного значения a (уровня значимости) и числа степеней свободы k.
Если расчетное значение 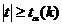 ,то нулевую гипотезу об отсутствии корреляционной связи следует отвергнуть; переменные считают зависимыми.
,то нулевую гипотезу об отсутствии корреляционной связи следует отвергнуть; переменные считают зависимыми.
|
из
5.00
|
Обсуждение в статье: Проверка гипотезы о равенстве средних (сравнение результатов измерений) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

