 |
Главная |
Дифференциальная модель квазивидов
|
из
5.00
|
Одна из наиболее известных моделей квазивидов – модель, описывающая достаточно простую эволюцию полинуклеотидных последовательностей. Характер эволюции существенно зависит от численности популяции. Если последняя велика, эволюция может рассматриваться как детерминированный процесс. В этом случае эволюционная динамика популяции может быть описана системой обыкновенных дифференциальных уравнений (ОДУ).
Предположим, что существует n различных последовательностей нуклеиновых кислот 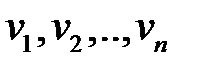 . Каждая разновидность (вариант) характеризуется определенной последовательностью нуклеотидов, которая определяет скорость репликации данной разновидности.
. Каждая разновидность (вариант) характеризуется определенной последовательностью нуклеотидов, которая определяет скорость репликации данной разновидности.
Обозначим скорости репликации разновидностей 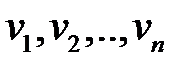 как
как  соответственно. В отсутствие мутации разновидность с самой высокой скоростью репликации будет расти быстрее и достигнет размера популяции. Результатом отбора (без ошибок) является однородная популяция, состоящая из генотипа, обладающего наибольшей скоростью репликации.
соответственно. В отсутствие мутации разновидность с самой высокой скоростью репликации будет расти быстрее и достигнет размера популяции. Результатом отбора (без ошибок) является однородная популяция, состоящая из генотипа, обладающего наибольшей скоростью репликации.
Но репликация не лишена ошибок. Таким образом, необходимо определить вероятности 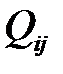 того, что на очередном шаге репликации цепочка РНК вида
того, что на очередном шаге репликации цепочка РНК вида 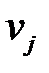 в результате мутации станет цепочкой вида
в результате мутации станет цепочкой вида  . Вероятности
. Вероятности 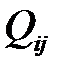 для i=1,2,..,n и j=1,2,..,n формируют так называемую «матрицу мутации».
для i=1,2,..,n и j=1,2,..,n формируют так называемую «матрицу мутации».
Репликации квазивидов могут быть представлены следующими реакциями:
безошибочный вариант: 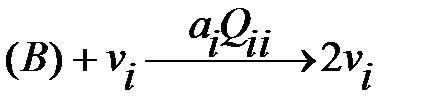 ,
,
мутация: 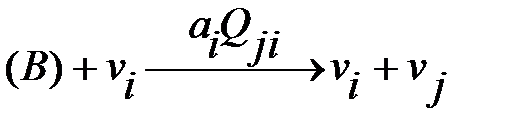 .
.
Символ В обозначает материалы с низким молекулярным весом (это четыре нуклеотида), которые требуются для синтеза РНК или ДНК. Предполагается, что доступное количество (нужный объём) В является постоянным и, следовательно, не будет использован в кинетических дифференциальных уравнениях. Без ошибок репликации и мутации – это параллельные реакции одного и того же механизма. Вероятности мутации 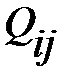 влияют на продукт репликации. Коэффициент
влияют на продукт репликации. Коэффициент 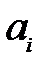 описывает скорость репликации генома с номером
описывает скорость репликации генома с номером  .
.
Система обыкновенных дифференциальных уравнений, описывающая развитие (эволюцию) во времени популяции этих последовательностей нуклеиновых кислот, может быть записана в виде
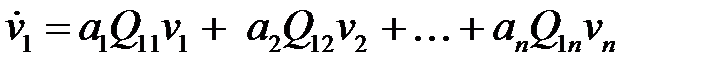 . (2.1)
. (2.1)
Новые частицы разновидности (варианта) 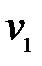 могут быть образованы в результате безошибочной репликации
могут быть образованы в результате безошибочной репликации 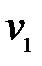 . Это происходит при скорости
. Это происходит при скорости 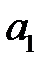 и вероятности
и вероятности 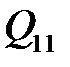 , поэтому общая скорость воспроизводства цепочек вида
, поэтому общая скорость воспроизводства цепочек вида 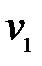 –
– 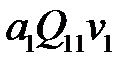 . Ошибочная репликация любых других мутантов
. Ошибочная репликация любых других мутантов  может также привести к появлению новых вирусных частиц
может также привести к появлению новых вирусных частиц 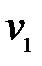 . Это представлено ростом темпов в уравнении (2.1). Таким же образом можно записать скорость производства любых других разновидностей и получить систему дифференциальных уравнений:
. Это представлено ростом темпов в уравнении (2.1). Таким же образом можно записать скорость производства любых других разновидностей и получить систему дифференциальных уравнений:
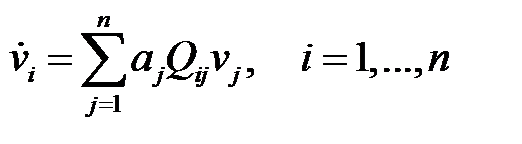 . (2.2)
. (2.2)
Вероятность мутации определяется по формуле
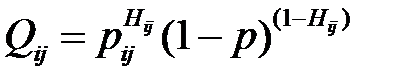 . (2.3)
. (2.3)
Здесь 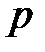 –скорость мутации в расчёте на одно основание,
–скорость мутации в расчёте на одно основание, 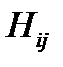 – это расстояние Хэмминга между штаммами i и j, то есть количество оснований, в котором две линии отличаются. Расстояние Хемминга определяется следующим образом:
– это расстояние Хэмминга между штаммами i и j, то есть количество оснований, в котором две линии отличаются. Расстояние Хемминга определяется следующим образом:
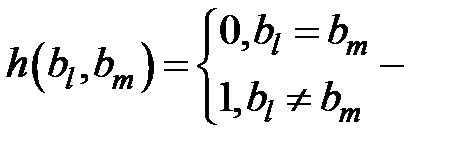 – для двух оснований,
– для двух оснований,
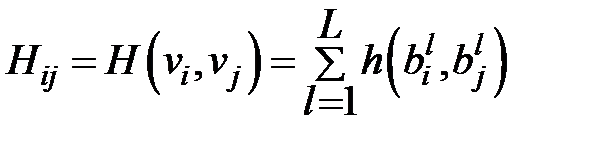 для двух генов
для двух генов 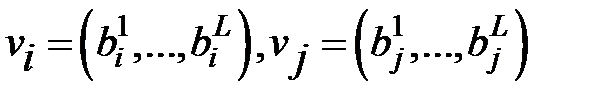 .
.
Без ошибок репликация задаётся формулой
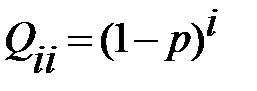 . (2.4)
. (2.4)
Популяция не будет состоять только из наиболее быстро растущей последовательности, напротив, она будет состоять из целого ансамбля мутантов с различными скоростями репликации. Это ансамбль мутантов – квазивидов.
Частота появления того или иного варианта внутри квазивидов зависит не только от его импликативного значения, но также и от вероятности, с которой он производится ошибочной репликацией других шаблонов и их частоты в распределении квазивидов. Это важно для понимания структурной организации квазивидов.
Квазивиды сами по себе являются целью отбора в процессе воспроизводства популяции. Этот факт имеет большое значение. Эволюция, как правило, рассматривается как взаимодействие между процессами мутации и отбора. Отбор – фактор, который способствует преимуществам мутантов, которые были собраны по чистой случайности.
В рамках теории квазивидов, использующей аппарат обыкновенных дифференциальных уравнений, можно эффективно исследовать влияние мутаций на генетическую эволюцию вирусных популяций [8].
6 Адаптация дифференциальной модели
Характер популяционной эволюции существенно зависит от численности популяции n. Если n очень велико, то численности особей каждого вида можно рассматривать как большие числа. В этом случае эволюционная динамика популяции может быть описана системой обыкновенных дифференциальных уравнений (ОДУ).
Будем называть виртуальным геномом последовательность символов, которая кодирует некоторый участок РНК вируса иммунодефицита человека. Далее будет использован четырехбуквенный алфавит, каждая буква которого соответствует нуклеотиду: A – аденин, G – гуанин, T – тимин, C – цитозин. В модели виртуальный ген является аналогом нити вирусной РНК, а виртуальная популяция (вектор пар виртуальных генов) – аналог вирусных частиц.
Как и в работе [11], рассматриваются вирусные мутанты, резистентные к действию зидовудина (AZT),блокирующего обратную транскрипцию вирусной РНК в ДНК, ограниченного спектра: в 41 и 215 позициях аминокислотной последовательности находятся метионин (ATG) и треонин (ACC) соответственно, т.е. вирусы начальной популяции позициях 121–123 содержат комбинацию символов ATG, а в позициях 643–645 – комбинацию символов ACC.
Рассматриваемая популяция подразделяется на восемь классов:
WT (дикий тип – в 41 и 215 позициях находятся метионин (ATG) и треонин (ACC) соответственно, т.е. в позициях 121–123 содержится комбинация символов ATG, а в позициях 643–645 – комбинация символов ACC);
M41L (в 41 позиции последовательность TTG);
T215N (в 215 позиции последовательность ААС);
T215S (в 215 позиции последовательность ТСС);
T215Y (в 215 позиции последовательность TAC);
M41L/T215N (в 41 позиции последовательность TTG, в 215 позиции последовательность AAC);
M41L/T215S (в 41 позиции последовательность TTG, в 215 позиции последовательность TCC);
M41L/T215Y (в 41 позиции последовательность TTG, в 215 позиции последовательность TAC).
Рассмотрим модель следующего вида, предложенную в работе NovakM.A. [8]:
Уравнения теории квазивидов имеют вид:
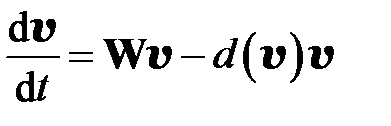 . (3.1)
. (3.1)
Вектор 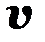 содержит в качестве компонентов численности генотипов, составляющих популяцию
содержит в качестве компонентов численности генотипов, составляющих популяцию 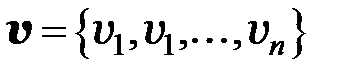 , матрица
, матрица  имеет вид
имеет вид
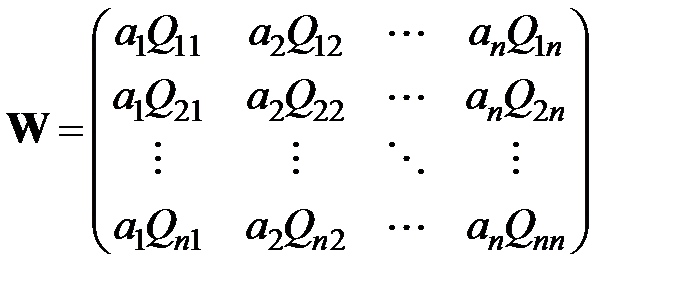 . (3.2)
. (3.2)
Здесь  – численность i-го квазивида в вирусной популяции, где
– численность i-го квазивида в вирусной популяции, где 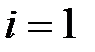 соответствует дикому типу (WT),
соответствует дикому типу (WT), 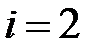 – мутанту M41L,
– мутанту M41L, 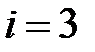 – T215N,
– T215N, 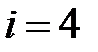 – T215S,
– T215S,  – T215Y,
– T215Y, 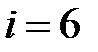 – M41L+T215N,
– M41L+T215N, 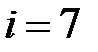 – M41L+T215S,
– M41L+T215S, 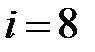 – M41L+T215Y;
– M41L+T215Y; 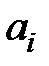 ‑ скорость репликации i-го квазивида;
‑ скорость репликации i-го квазивида; 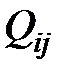 ‑ вероятность того, что мутант j-го типа станет мутантом i-го типа.
‑ вероятность того, что мутант j-го типа станет мутантом i-го типа.
Второе слагаемое в правой части (3.1) вводится для сохранения постоянства численности популяции
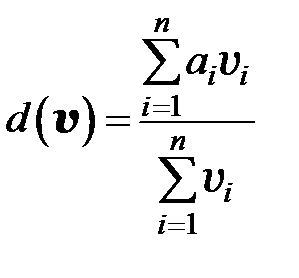 . (3.3)
. (3.3)
Для различной численности популяции система решалась при следующих начальных условиях:
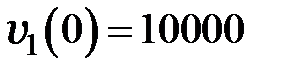 ,
, 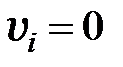 ,
, 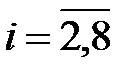 , (3.4)
, (3.4)
что соответствует в начальный момент времени однородной популяции, состоящей из дикого типа;
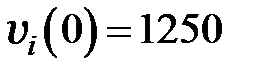 ,
, 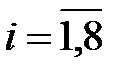 , (3.5)
, (3.5)
что соответствует разнородной популяции, содержащей в начальный момент времени одинаковое количество геномов каждого типа.
В качестве значений скоростей репликации геномов 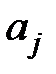
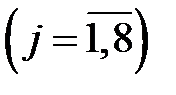 могут быть взяты экспериментальные данные из работы [10], приведенные в таблице 3.
могут быть взяты экспериментальные данные из работы [10], приведенные в таблице 3.
Таблица 3 – Значения функции приспособленности для AZT-резистентных мутантов
| Концентрация AZTмM | Дикий тип WT | Мутация вида M41L | Мутация вида T215N | Мутация вида T215S | Мутация вида T215Y | Мутация вида M41L+ T215N | Мутация вида M41L+ T215S | Мутация вида M41L+ T215Y |
| 0,60398 | 0,20344 | 0,25286 | 0,70386 | 0,29144 | 0,49304 | 0,78211 | ||
| 0,03 | 0,56022 | 0,50883 | 0,095828 | 0,10023 | 0,60567 | 0,12426 | 0,39282 | 0,61736 |
| 0,3 | 0,16226 | 0,16627 | 0,011927 | 0,01554 | 0,29251 | 0,038069 | 0,11565 | 0,38495 |
| 0,042648 | 0,023637 | 0,00092379 | 0,0038235 | 0,11608 | 0,020068 | 0,00923 | 0,18732 | |
| 0,0052242 | 0,011629 | 0,02723 | 0,0011425 | 0,0029013 | 0,097714 | |||
| 10,000 | 0,0010917 | 0,010589 | 0,020544 |
Вероятности переходов от одного типа мутанта к другому 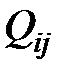 оцениваются следующим образом. Вероятность замены одного основания на другое в конкретной позиции
оцениваются следующим образом. Вероятность замены одного основания на другое в конкретной позиции 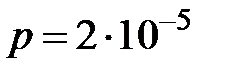 на один нуклеотид [9]. Так как используется четырехбуквенный код (A, C, G, T), то каждое основание может быть заменено одним из трех других. И вероятность того, что мутация произойдет в заданной позиции, равна
на один нуклеотид [9]. Так как используется четырехбуквенный код (A, C, G, T), то каждое основание может быть заменено одним из трех других. И вероятность того, что мутация произойдет в заданной позиции, равна 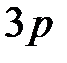 . Вероятность того, что ни в одной из позиций (41-й или 215-й) ни одно из кодирующих оснований не изменится, равна
. Вероятность того, что ни в одной из позиций (41-й или 215-й) ни одно из кодирующих оснований не изменится, равна 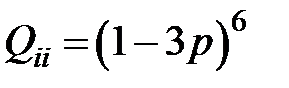 . Вероятность конкретной мутации в одном из шести рассматриваемых оснований равна
. Вероятность конкретной мутации в одном из шести рассматриваемых оснований равна 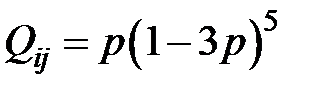 . Если для перехода от одного мутанта к другому необходимо более двух мутаций, считается, что вероятность такого перехода равна нулю. Далее для всех моделей использованы приведенные значения вероятностей переходов от одного типа мутанта к другому. С учётом этих условий получаем преобразованную модель в следующем виде:
. Если для перехода от одного мутанта к другому необходимо более двух мутаций, считается, что вероятность такого перехода равна нулю. Далее для всех моделей использованы приведенные значения вероятностей переходов от одного типа мутанта к другому. С учётом этих условий получаем преобразованную модель в следующем виде:
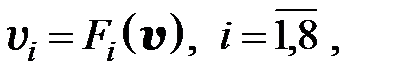
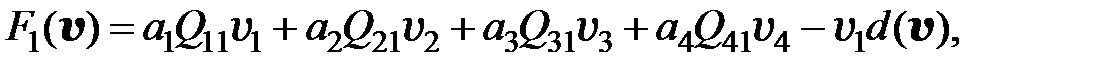
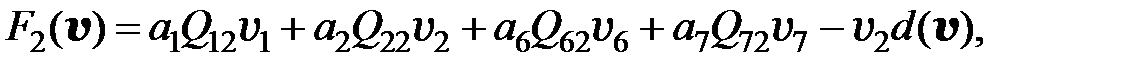
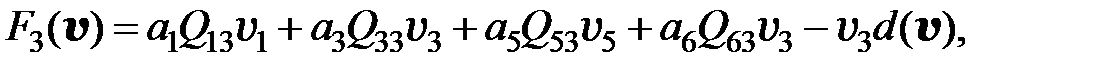
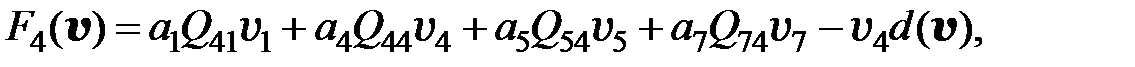
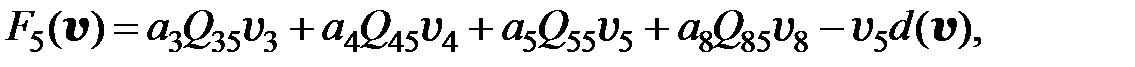 (3.6)
(3.6)
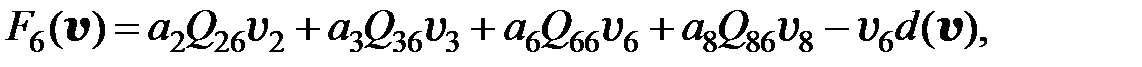
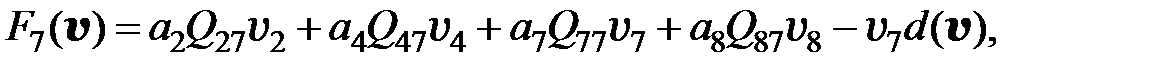
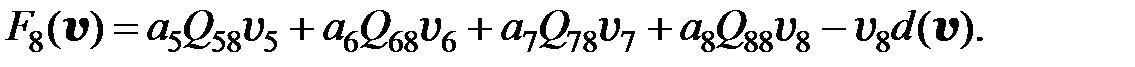
Если считать концентрацию противовирусного препарата в организме пациента постоянной, (3.6) является системой ОДУ с постоянными коэффициентами. Для исследования динамики популяции следует задать начальные условия – размеры субпопуляций (численности каждого квазивида) до начала терапии.
Далее система (3.6) решается для случая изначально однородной популяции при условиях (3.4) и разнородной популяции при условиях (3.5).
На основе численных экспериментов, изменяя начальные условия и параметры модели (коэффициенты 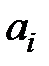 зависят от условий среды, в которой находится популяция), можно изучить влияние биологических характеристик системы на ее динамику.
зависят от условий среды, в которой находится популяция), можно изучить влияние биологических характеристик системы на ее динамику.
Для численного решения системы уравнений использовался алгоритм ode15s для решения жёстких систем ОДУ [12, 13], реализованный в пакете MATLAB. Это многошаговый метод переменного порядка (от 1 до 5, по умолчанию 5), использующий формулы численного дифференцирования. Решением соответствующей начальной задачи являются функции, описывающие эволюцию численности популяций соответствующих мутантов.
Численные результаты
Упрощающее анализ предположение о постоянстве концентрации препарата AZT в организме человека не вполне реалистично. В действительности, после приёма препарата его концентрация резко возрастает, а потом, по мере выведения лекарства из организма, падает, что, в свою очередь, отражается на скорости репликации мутантов и динамике изменения их численности.
|
из
5.00
|
Обсуждение в статье: Дифференциальная модель квазивидов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

