 |
Главная |
Удаление узла из списка
|
из
5.00
|
a) первого узла
start

TelNum *del = start;
start = start->next;
delete del;
b) В середине писка
 |
current del
TelNum *del = current->next;
current->next = del->next;
delete del;
c) в конце списка
 current end
current end
TelNum *del = end;
current->next=NULL;
delete del;
end = current;
Алгоритмы, приведенные выше, обладают существенным недостатком - если необходимо произвести вставку или удаление ПЕРЕД заданным узлом, то так как неизвестен адрес предыдущего узла, невозможно получить доступ к указателю на удаляемый (вставляемый) узел и для его поиска надо произвести обход списка, что для больших списков неэффективно. Избежать этого позволяет двунаправленный список, который имеет два указателя: один - на последующий узел, другой - на предыдущий.
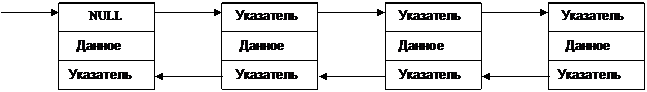 |
start
NULL
// Пример программы работы с односвязным списком
#include <stdio.h>
#include <conio.h>
struct TelNum;
int printAllData(TelNum * start);
int inputData(TelNum * n);
struct TelNum
{
TelNum * next;
long number;
char name[30];
};
// Описание: печать списка
int printAllData(TelNum * start){
int c=0;
for(TelNum * t=start;t; t= t->next)
printf("#%3.3i %7li %s\n",++c,t->number,t->name);
return 0;
}
// Описание: ввод данных в структуру n конец ввода - ввод нуля
// в первое поле. Возвращает 1 если конец ввода
int inputData(TelNum * n){
printf("Номер?"); scanf("%7li",&n->number);
if(!n->number) return 1;
printf("Имя? "); scanf("%30s",&n->name);
return 0;
}
void main(void){
TelNum * start = NULL; //сторож
TelNum * end = start;
do{ //блок добавления записей
TelNum * temp = new TelNum;
if(inputData(temp)) {
delete temp;
break;
}
else {
if(start==NULL) {
temp->next = start;
start = temp;
end = temp;
}
else {
end->next=temp;
end=temp;
end->next=NULL;
}
}
}while(1);
printf("\nЗаписи после добавления новых:\n");
printAllData(start);
getch();
do{ //блок удаления записей
TelNum * deleted = start;
start = start->next;
delete deleted;
printAllData(start);
getch();
}while(start!=NULL);
}
Бинарные деревья
В бинарном дереве каждый узел содержит 2 указателя. Начальная точка бинарного дерева называется корневым узлом.
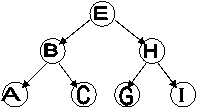 |
Корневой узел Е указывает на В и Н. Узел В является корневым узлом для левого поддерева Е, узел Н – для правого поддерева Е. За исключением самого нижнего яруса каждый узел бинарного дерева имеет одно или два поддерева.
Обычно левое поддерево содержит меньшие данные, правое большие, что ускоряет поиск информации. Дерево такого типа называется деревом бинарного поиска.
Поиск обычно начинается с корня. В зависимости от результата сравнения двигаются либо влево (если данные узла больше образца поиска), либо вправо (если меньше). Новые узлы всегда присоединяются к нижним вершинам, так что дерево всегда растет вниз.
Чтобы распечатать бинарное дерево можно использовать алгоритм, называемый обратным ходом. Простейший алгоритм - рекурсивный. При заданном корне, программа совершает 3 шага:
а) выполняет обход левого поддерева;
б) печать корня;
в) выполняет обход правого поддерева.
Если обнаружен указатель NULL, то продвижение в направлении обхода в данном поддереве прекращается.
При прямом обходе содержимое корня печатается до обхода поддеревьев.
При концевом обходе содержимое корня печатается после совершения обхода двух поддеревьев.
// Пример программы работы с бинарным деревом
#include <stdio.h>
#include <conio.h>
#include <string.h>
struct TelNum;
void printtreepre(TelNum * ); //обход с корня дерева, левое поддерево, правое поддерево
void printtreein(TelNum * ); //обход с вершины правое поддерево,корень, левое поддерево
void printtreepost(TelNum * ); //обход с вершины левое поддерево, правое поддерево,корень
int inputData(TelNum * );
TelNum * addtree(TelNum *, TelNum *);
struct TelNum
{
TelNum * left, *right;
long number;
char name[30];
};
// Описание: печать списка
void printtreepre(TelNum * root)
{
if(!root) return;
if(root->number)
printf("номер %7li фамилия %s\n",root->number,root->name);
printtreepre(root->left);
printtreepre(root->right);
}
void printtreein(TelNum * root)
{
if(!root) return;
if(root->number)
printtreein(root->left);
printf("номер %7li фамилия %s\n",root->number,root->name);
printtreein(root->right);
}
void printtreepost(TelNum * root)
{
if(!root) return;
if(root->number)
printtreepost(root->left);
printtreepost(root->right);
printf("номер %7li фамилия %s\n",root->number,root->name);
}
// Описание: ввод данных
int inputData(TelNum * n)
{
printf("Номер?"); scanf("%7li",&n->number);
if(!n->number) return 1;
printf("Имя? "); scanf("%30s",&n->name);
return 0;
}
// Добавление узла к дереву
TelNum * addtree(TelNum *root, TelNum *temp) {
if(root==NULL) { //добавление узла в вершину дерева
TelNum * root = new TelNum;
root->number=temp->number;
strcpy(root->name,temp->name);
root->left=NULL;
root->right=NULL;
return root;
}
else {
if(root->number>temp->number)
root->left=addtree(root->left,temp);
else root->right=addtree(root->right,temp);
}
return root;
}
// Поиск значения в бинарном дереве
//по номеру телефона
void searchtree(TelNum *root, int num) {
while (root!=NULL) {
if(root->number==num) {
printf("номер %7li фамилия %s\n",root->number,root->name);
return ;
}
else{
if(root->number>num)
root=root->left;
else root=root->right;
}
}
puts("Телефон не найден");
return ;
}
void main(void)
{
TelNum * start = NULL; //сторож
TelNum * temp = new TelNum;
do{ //блок добавления записей
if(inputData(temp))
{delete temp;
break;
}
else
start=addtree(start,temp);
}while(1);
printtreepre(start); //ebcahgi
getch();
printtreein(start); //ighebca
getch();
printtreepost(start); //acbighe
getch();
int num;
puts("Введите номер телефона");
scanf("%d",&num);
searchtree(begin,num);
}
|
из
5.00
|
Обсуждение в статье: Удаление узла из списка |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

