Энтропия. Формула Больцмана.

Энтропия – это ф-ия состояния системы. Приведенная теплота: dQ/T, где dQ- теплота получаемая телом в изотермическом процессе, Т- температура теплоотдающего тела, если система обратима, переходит из состояния А в В, то интеграл от приведенной теплоты не зависит от пути перехода из одного состояния в другое: _.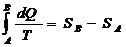

Для кругового обратимого процесса S_В=S_A сл-но, 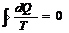, dQ/T-полный дифференциал некоторой ф-ии S, которая определяется т-ко состоянием системы и не зависит от пути, которым система пришла в это состояние, сл-но, S-это ф-ия состояния. dQ/T=dS. Термен энтропия введен Клаузисом как мера способности теплоты превращаться в другие меры энергии, энтропия обладает свойством аддитивности: S системы =сумме составляющих систему.

Энтропия идеального газа для изохоры: V=const, ΔS=C_v *ln(T₂/T₁).

Для изобары: P=const, ΔS=C_v *ln(T₂/T₁ )+ R*ln(V₂/V₁).

Для изотермы: T=const, ΔS=R*ln(V₂/V₁).

Больцман доказал (1872), что между энтропией системы и термодинамической вероятностью её состояния существует связь, которая называется формулой Больцмана: S=k*lnP, где k – постоянная Больцмана.

Формула Больцмана позволяет дать статистическое истолкование второго закона термодинамики, утверждающего, что энтропия изолированной системы не убывает: термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать.

Следовательно, при всяком процессе, протекающем в изолированной системе,

Изменение термодинамической вероятности ее состояния ΔР положительно или равно нулю: ΔР = Р₂-Р₁ ≥0

Для обратимого процесса ΔР=0 и P=const, а в случае необратимого процесса ΔР>0 и Р возрастает. Следовательно, необратимый процесс — процесс, при котором система из менее вероятного состояния переходит в более вероятное, в пределе — в равновесноесостояние. Иначе его можно определить как процесс, обратный тому, при котором система из более вероятного состояния переходит в менее вероятное. Самопроизвольное протекание обратного процесса маловероятно, хотя в принципе и возможно. Чтобы он произошел, требуется одновременное протекание компенсирующего процесса вовнешних телах. По второму закону термодинамики, компенсирующий процесс должен быть таким, чтобы термодинамическая вероятность состояния системы всех тел, участвующих в осуществлении обратного и компенсирующего процессов, возрастала.

28. Закон возрастания энтропии. Гипотеза о тепловой смерти Вселенной.

1.В адиабатически изолированной системе энтропия системы при обратимых процессах не меняется, а при необратимых процессах возрастает: dS≥0.Обратимый процесс dQ=0=>dS=dQ/t=0; необратимый процесс dS>0. процессы в замкнутой системе идут в направлении увеличения числа микросостояний, т.е. от менее вероятных состояний к более вероятным до тех пор, пока вероятность состояния не станет максимальной.

2.Если система не замкнутая, то dS≥dQ/T. Уравнения 1 и 2 это аналитическая запись 2-го начала термодинамики. Примеры возрастания энтропии:

Теплопроводность: ∆Q1=∆Q2=∆Q

∆Q

∆Q/T1 ∆Q/T2